Двусвязный граф - Biconnected graph
| Актуальные темы на |
| Связь с графиком |
|---|
В теория графов, а двусвязный граф является связным и «неразделимым» график, что означает, что если кто-то вершина были удалены, граф останется связанным. Следовательно, двусвязный граф не имеет вершины сочленения.
Свойство быть 2-связный эквивалентно двусвязности, за исключением того, что полный график двух вершин обычно не считается 2-связным.
Это свойство особенно полезно при поддержании графа с двойным избыточность, чтобы предотвратить отключение при удалении одного край (или подключение).
Использование двусвязный графики очень важны в области сетевых технологий (см. Сетевой поток ) из-за этого свойства избыточности.
Определение
А двусвязный неориентированный граф является связным графом, который не разбивается на несвязные части путем удаления любой единственной вершины (и ее инцидентных ребер).
А двусвязный ориентированный граф такое, что для любых двух вершин v и ш есть два направленных пути от v к ш которые не имеют общих вершин, кроме v и ш.
| Вершины | Количество возможностей |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 1 |
| 4 | 3 |
| 5 | 10 |
| 6 | 56 |
| 7 | 468 |
| 8 | 7123 |
| 9 | 194066 |
| 10 | 9743542 |
| 11 | 900969091 |
| 12 | 153620333545 |
| 13 | 48432939150704 |
| 14 | 28361824488394169 |
| 15 | 30995890806033380784 |
| 16 | 63501635429109597504951 |
| 17 | 244852079292073376010411280 |
| 18 | 1783160594069429925952824734641 |
| 19 | 24603887051350945867492816663958981 |
Примеры

Двусвязный граф с четырьмя вершинами и четырьмя ребрами

Граф, который не двусвязен. Удаление вершины x отключит граф.

Двусвязный граф с пятью вершинами и шестью ребрами
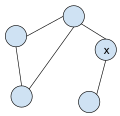
Граф, который не двусвязен. Удаление вершины x отключит граф.
Смотрите также
Рекомендации
- Эрик В. Вайсштейн. «Двусвязный граф». Материал из MathWorld - веб-ресурса Wolfram. http://mathworld.wolfram.com/BiconnectedGraph.html
- Пол Э. Блэк, «двусвязный граф», в Словаре алгоритмов и структур данных [онлайн], Пол Э. Блэк, изд., Национальный институт стандартов и технологий США. 17 декабря 2004 г. (доступ СЕГОДНЯ) Доступно по: https://xlinux.nist.gov/dads/HTML/biconnectedGraph.html
внешняя ссылка
- Дерево двусвязных компонентов Java-реализация в библиотеке jBPT (см. класс BCTree).
