График Биггса – Смита - Biggs–Smith graph
| График Биггса – Смита | |
|---|---|
 Граф Биггса – Смита | |
| Вершины | 102 |
| Края | 153 |
| Радиус | 7 |
| Диаметр | 7 |
| Обхват | 9 |
| Автоморфизмы | 2448 (PSL (2,17)) |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Характеристики | Симметричный Дистанционно-регулярный Кубический Гамильтониан |
| Таблица графиков и параметров | |
в математический поле теория графов, то График Биггса – Смита это 3-регулярный граф со 102 вершинами и 153 ребрами.[1]
Он имеет хроматическое число 3, хроматический индекс 3, радиус 7, диаметр 7 и обхват 9. Это также 3-вершинно-связный граф и 3-реберный граф.
Все кубический дистанционно регулярные графы известны.[2] Граф Биггса – Смита - один из 13 таких графов.
Алгебраические свойства
Группа автоморфизмов графа Биггса – Смита - это группа порядка 2448[3] изоморфен проективная специальная линейная группа PSL (2,17). Он действует транзитивно на вершинах, на ребрах и на дугах графа. Следовательно, граф Биггса – Смита является симметричный граф. У него есть автоморфизмы, которые переводят любую вершину в любую другую вершину и любое ребро в любое другое ребро. Согласно Приемная перепись, граф Биггса – Смита, обозначаемый как F102A, является единственным кубическим симметричным графом с 102 вершинами.[4]
Граф Биггса – Смита также однозначно определяется своим спектр графика, множество собственных значений графа его матрица смежности.[5]
В характеристический многочлен графа Биггса – Смита:.
Галерея

В хроматическое число графа Биггса – Смита равно 3.

В хроматический индекс графа Биггса – Смита равно 3.

Альтернативный рисунок графа Биггса – Смита.
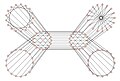
Разложение графа Биггса – Смита на 6 наборов размера 17.
Рекомендации
- ^ Вайсштейн, Эрик В. «График Биггса – Смита». MathWorld.
- ^ Брауэр, А.Э.; Коэн, А. М .; и Ноймайер А. Дистанционно регулярные графы. Нью-Йорк: Springer-Verlag, 1989.
- ^ Ройл, Г. Данные F102A[постоянная мертвая ссылка ]
- ^ Кондер, М. и Добчаньи П. «Трехвалентные симметричные графы до 768 вершин». J. Combin. Математика. Комбинировать. Comput. 40, 41–63, 2002.
- ^ Э. Р. ван Дам, В. Х. Хемерс, Спектральные характеристики некоторых дистанционно регулярных графов. J. Алгебраический комбинат. 15, страницы 189–202, 2003 г.
- О трехвалентных графах, Н.Л. Биггс, Д.Х. Смит - Бюллетень Лондонского математического общества, 3 (1971) 155-158.





