Фазовая автоподстройка заряда-насоса - Charge-pump phase-locked loop

Зарядный насос ФАПЧ

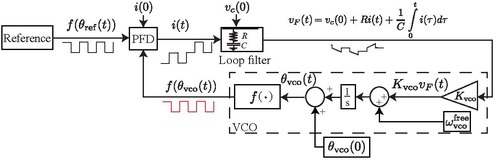
Фазовая автоподстройка заряда насоса (CP-PLL) является модификацией петли фазовой автоподстройки частоты с фазочастотный детектор и сигналы прямоугольной формы.^[1] CP-PLL позволяет быстро захватить фазу входящего сигнала, достигая низкой фазовой ошибки в установившемся состоянии.^[2]

Частотно-фазовый детектор (ЧФД)

Частотно-фазовый детектор динамики

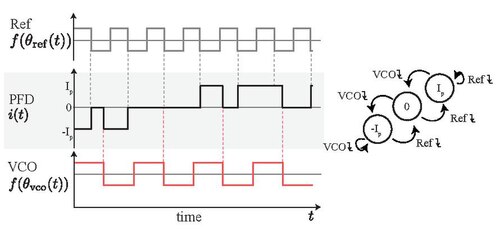
Фазовый детектор частоты (ПФО) инициируется задних кромок ссылки (REF) и контролируемых сигналов (ГУН). Выходной сигнал PFD ${ Displaystyle я (т)}$ может иметь только три состояния: 0, ${ displaystyle + I_ {p}}$, и ${ displaystyle -I_ {p}}$.A задней кромки опорного сигнала сил ПФО, чтобы переключиться на более высокое состояние, если он уже не в состоянии ${ displaystyle + I_ {p}}$. Задний фронт сигнала VCO заставляет PFD переключиться в более низкое состояние, если он уже не находится в состоянии ${ displaystyle -I_ {p}}$.Если оба задних фронта происходят одновременно, PFD переключается на ноль.

Математические модели CP-PLL

Первая линейная математическая модель CP-PLL второго порядка была предложена Ф. Гарднер в 1980 г.^[2] Нелинейная модель без перегрузки ГУН была предложена М. ван Пэмелем в 1994 г. ^[3]а затем уточнены Н. Кузнецовым и соавт. в 2019 году.^[4] Получена замкнутая математическая модель CP-PLL с учетом перегрузки ГУН в.^[5]

Эти математические модели CP-PLL позволяют получить аналитические оценки диапазона удержания (максимальный диапазон периода входного сигнала, при котором существует заблокированное состояние, в котором ГУН не перегружен) и диапазона втягивания ( максимальный диапазон периода входного сигнала в пределах диапазона удержания, так что для любого начального состояния CP-PLL принимает заблокированное состояние).^[6]

Линейная модель с непрерывным временем CP-PLL второго порядка и гипотеза Гарднера

Анализ Гарднера основан на следующем приближении:^[2] временный интервал, на котором ОФП имеет ненулевое состояние на каждый период опорного сигнала

${ displaystyle t_ {p} = | theta _ {e} | / omega _ { rm {ref}}, theta _ {e} = theta _ { rm {ref}} - theta _ { rm {vco}}.}$

Тогда усредненная мощность ПФД зарядовой накачки равна

${ displaystyle i_ {d} = I_ {p} theta _ {e} / 2 pi}$

с соответствующей передаточной функцией

${ Displaystyle I_ {d} (s) = I_ {p} theta _ {e} (s) / 2 pi}$

Использование передаточной функции фильтра ${ Displaystyle F (s) = R + { frac {1} {Cs}}}$ и передаточная функция VCO ${ displaystyle theta _ { rm {vco}} (s) = K _ { rm {vco}} I_ {d} (s) F (s) / s}$ получается линейная приближенная средняя модель Гарднера CP-PLL второго порядка

${ displaystyle { frac { theta _ {e} (s)} { theta _ { rm {ref}} (s)}} = { frac {2 pi s} {2 pi s + K_ { rm {vco}} I_ {p} left (R + { frac {1} {Cs}} right)}}.}$

В 1980 г. Ф. Гарднер, основываясь на приведенных выше рассуждениях, предположил, что переходный отклик практических ФАПЧ с накачкой заряда будет почти таким же, как отклик эквивалентной классической ФАПЧ.^[2]:1856 (Гипотеза Гарднера о CP-PLL ). Следуя результатам Гарднера, по аналогии с Гипотеза Игана о диапазоне втягивания APLL типа 2, Предположил Амр М. Фахим в своей книге^[7]:6 что для получения бесконечного диапазона втягивания (захвата) необходимо использовать активный фильтр для контурного фильтра в CP-PLL (гипотеза Фахима-Эгана о диапазоне втягивания в CP-PLL типа II).

Нелинейная модель непрерывного времени CP-PLL второго порядка

Без ограничения общности предполагается, что задние фронты сигналов VCO и Ref возникают, когда соответствующая фаза достигает целого числа. Пусть момент времени первого заднего фронта сигнала Ref определяется как ${ displaystyle t = 0}$. Состояние ПФО ${ displaystyle i (0)}$ определяется начальным состоянием ПФО ${ Displaystyle я (0-)}$, начальные фазовые сдвиги ГУН ${ displaystyle theta _ {vco} (0)}$ и Ref ${ displaystyle theta _ {ref} (0)}$ сигналы.

Связь между входным током ${ Displaystyle я (т)}$ и выходное напряжение ${ Displaystyle v_ {F} (т)}$ для пропорционально интегрирующего (совершенного PI) фильтра на основе резистора и конденсатора выглядит следующим образом

${ displaystyle { begin {align} v_ {F} (t) = v_ {c} (0) + Ri (t) + { frac {1} {C}} int limits _ {0} ^ { t} я ( тау) д тау конец {выровнено}}}$

где ${ displaystyle R> 0}$ это сопротивление, ${ displaystyle C> 0}$ это емкость, а ${ displaystyle v_ {c} (t)}$ - заряд конденсатора. управляющий сигнал ${ Displaystyle v_ {F} (т)}$ регулирует частоту VCO:

${ displaystyle { begin {align} { dot { theta}} _ {vco} (t) = omega _ {vco} (t) = omega _ {vco} ^ { text {free}} + K_ {vco} v_ {F} (t), end {align}}}$

где ${ displaystyle omega _ {vco} ^ { text {бесплатно}}}$ частота холостого хода ГУН (т. е. для ${ Displaystyle v_ {F} (т) экв 0}$), ${ displaystyle K_ {vco}}$- усиление (чувствительность) ГУН, а ${ Displaystyle theta _ {vco} (т)}$ - фаза ГУН. Наконец, нелинейная математическая модель непрерывного времени CP-PLL выглядит следующим образом:

${ displaystyle { begin {align} { dot {v}} _ {c} (t) = { tfrac {1} {C}} i (t), quad { dot { theta}} _ {vco} (t) = omega _ {vco} ^ { text {free}} + K_ {vco} (Ri (t) + v_ {c} (t)) end {align}}}$

со следующей разрывной кусочно-постоянной нелинейностью

${ Displaystyle я (т) = я { большой (} я (т -), тета _ {ref} (т), тета _ {vco} (т) { большой)}}$

и начальные условия ${ displaystyle { big (} v_ {c} (0), theta _ {vco} (0) { big)}}$.Эта модель представляет собой нелинейную, неавтономную, прерывистую систему переключения.

Нелинейная модель с дискретным временем CP-PLL второго порядка

Временные интервалы динамики ПФО.

Предполагается, частоты опорного сигнала постоянной:${ displaystyle theta _ {ref} (t) = omega _ {ref} t = { frac {t} {T_ {ref}}},}$где ${ displaystyle T_ {ref}}$, ${ displaystyle omega _ {ref}}$ и ${ Displaystyle theta _ {ref} (т)}$это период, частота и фаза опорного signal.Let ${ displaystyle t_ {0} = 0}$. Обозначим через ${ displaystyle t_ {0} ^ { rm {средний}}}$ первый момент времени, когда выход PFD становится нулевым (если ${ Displaystyle I (0) = 0}$, тогда ${ displaystyle t_ {0} ^ { rm {middle}} = 0}$) и ${ displaystyle t_ {1}}$ первый задний фронт ГУН или Ref. Далее соответствующие возрастающие последовательности ${ Displaystyle {т_ {к} }}$ и ${ displaystyle {t_ {k} ^ { rm {middle}} }}$ за ${ Displaystyle к = 0,1,2 ...}$ определены. ${ Displaystyle т_ {к} <т_ {к} ^ { rm {средний}}}$.Тогда для ${ displaystyle t in [t_ {k}, t_ {k} ^ { rm {middle}})}$ то ${ Displaystyle { текст {знак}} (я (т))}$ - ненулевая константа (${ displaystyle pm 1}$Обозначить ${ Displaystyle тау _ {к}}$ ширина импульса PFD (длина временного интервала, где выход PFD является ненулевой константой), умноженный на знак выхода PFD: т.е. ${ displaystyle tau _ {k} = (t_ {k} ^ { rm {middle}} - t_ {k}) { text {sign}} (i (t))}$ за ${ displaystyle t in [t_ {k}, t_ {k} ^ { rm {middle}})}$ и${ Displaystyle тау _ {к} = 0}$ за ${ displaystyle t_ {k} = t_ {k} ^ { rm {middle}}}$.Если задний фронт VCO попадает перед задним фронтом Ref, тогда ${ Displaystyle тау _ {к} <0}$ а в противном случае имеем ${ displaystyle tau _ {k}> 0}$, т.е. ${ Displaystyle тау _ {к}}$ показывает, как один сигнал отстает от другого. Нулевой выход PFD ${ Displaystyle я (т) эквив 0}$ на интервале ${ displaystyle (t_ {k} ^ { rm {middle}}, t_ {k + 1})}$:${ Displaystyle v_ {F} (т) эквив v_ {к}}$ за ${ displaystyle t in [t_ {k} ^ { rm {middle}}, t_ {k + 1})}$.Преобразование переменных^[8] ${ Displaystyle ( тау _ {к}, v_ {к})}$ к${ displaystyle p_ {k} = { frac { tau _ {k}} {T _ { rm {ref}}}}, u_ {k} = T _ { rm {ref}} ( omega _ { rm {vco}} ^ { text {free}} + K _ { rm {vco}} v_ {k}) - 1,}$позволяет сократить количество параметров до двух:${ displaystyle alpha = K _ { rm {vco}} I_ {p} T _ { rm {ref}} R, beta = { frac {K _ { rm {vco}} I_ {p} T _ { rm {ref}} ^ {2}} {2C}}.}$Здесь ${ displaystyle p_ {k}}$ - нормализованный фазовый сдвиг и ${ displaystyle u_ {k} +1}$ отношение частоты ГУН ${ displaystyle omega _ { rm {vco}} ^ { text {free}} + K _ { rm {vco}} v_ {k}}$ к опорной частоте ${ displaystyle { frac {1} {T _ { rm {ref}}}}}$Наконец, дискретная модель CP-PLL второго порядка без перегрузки ГУН.^[4][6]

${ displaystyle { begin {align} & u_ {k + 1} = u_ {k} +2 beta p_ {k + 1}, & p_ {k + 1} = { begin {cases} { frac { - (u_ {k} + alpha +1) + { sqrt {(u_ {k} + alpha +1) ^ {2} -4 beta c_ {k}}}} {2 beta}}, quad { text {for}} p_ {k} geq 0, quad c_ {k} leq 0, { frac {1} {u_ {k} +1}} - 1+ (p_ { k} { text {mod}} 1), quad { text {for}} p_ {k} geq 0, quad c_ {k}> 0, l_ {k} -1, quad { text {for}} p_ {k} <0, quad l_ {k} leq 1, { frac {- (u_ {k} + alpha +1) + { sqrt {(u_ {k } + alpha +1) ^ {2} -4 beta d_ {k}}}} {2 beta}}, quad { text {for}} p_ {k} <0, quad l_ {k }> 1, end {case}} end {align}}}$

где

${ displaystyle { begin {align} c_ {k} = (1- (p_ {k} { text {mod}} 1)) (u_ {k} +1) -1, S_ {l_ {k}} = - (u_ {k} - alpha +1) p_ {k} + beta p_ {k} ^ {2}, l_ {k} = { frac {1- (S_ {l_ {k}} { текст {mod}} 1)} {u_ {k} +1}}, d_ {k} = (S_ {l_ {k}} { text {mod}} 1) + u_ {k}. end {выровнено }}}$

Эта модель с дискретным временем имеет единственное устойчивое состояние при ${ displaystyle (u_ {k} = 0, p_ {k} = 0)}$ и позволяет оценить диапазоны удержания и удержания.^[6]

Если ГУН перегружен, т.е. ${ Displaystyle { точка { theta}} _ { rm {vco}} (т)}$ равно нулю, или что то же самое: ${ displaystyle (p_ {k}> 0, u_ {k} <2 beta p_ {k} -1)}$ или${ displaystyle (p_ {k} <0, u_ {k} < alpha -1)}$, то необходимо учитывать дополнительные случаи динамики CP-PLL.^[5]Для любых параметров перегрузка ГУН может возникнуть при достаточно большой разнице частот между ГУН и опорным сигналом. На практике перегрузки ГУН следует избегать.

Нелинейные модели CP-PLL высокого порядка

Вывод нелинейных математических моделей CP-PLL высокого порядка приводит к трансцендентным уравнениям, которые не могут быть решены аналитически без использования приближений.^[9]

Рекомендации