Кластеризация потока данных - Википедия - Data stream clustering
В Информатика, кластеризация потока данных определяется как кластеризация данных, которые поступают непрерывно, таких как телефонные записи, мультимедийные данные, финансовые транзакции и т. д. Кластеризация потоков данных обычно изучается как алгоритм потоковой передачи и цель состоит в том, чтобы, учитывая последовательность точек, построить хорошую кластеризацию потока с использованием небольшого количества памяти и времени.
История
Кластеризация потоков данных недавно привлекла внимание к новым приложениям, которые включают большие объемы потоковых данных. Для кластеризации k-означает - широко используемая эвристика, но были также разработаны альтернативные алгоритмы, такие как k-medoids, ИЗЛЕЧИВАТЬ и популярные[нужна цитата ] БЕРЕЗА. Для потоков данных один из первых результатов появился в 1980 г.[1] но модель была формализована в 1998 году.[2]
Определение
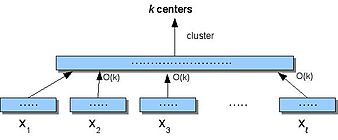
Проблема кластеризации потока данных определяется как:
Вход: последовательность п точки в метрическом пространстве и целое число k.
Выход: k центров в наборе п точек, чтобы минимизировать сумму расстояний от точек данных до их ближайших центров кластера.
Это потоковая версия задачи k-медианы.
Алгоритмы
ТРАНСЛИРОВАТЬ
STREAM - это алгоритм кластеризации потоков данных, описанный Гухой, Мишрой, Мотвани и О'Каллаганом.[3] который достигает приближение постоянного множителя для задачи k-Median за один проход и на небольшом пространстве.
Теорема — СТРИМ может решить k-Средняя проблема с потоком данных за один проход, со временем О(п1+е) и пробел θ(пε) с коэффициентом 2O (1 /е), куда п количество баллов и .
Чтобы понять STREAM, первым делом нужно показать, что кластеризация может происходить в небольшом пространстве (не заботясь о количестве проходов). Small-Space - это алгоритм разделяй и властвуй который разделяет данные, S, в частей, объединяет каждую из них (используя k-среднее), а затем кластеры полученные центры.
Алгоритм Small-Space (S)
- Разделять S в непересекающиеся части .
- Для каждого я, найти центры в Икся. Назначьте каждую точку в Икся до ближайшего центра.
- Позволять ИКС' быть центры, полученные в (2), где каждый центр c взвешивается по количеству присвоенных ему баллов.
- Кластер ИКС' найти k центры.
Где, если на шаге 2 мы запускаем бикритерию -алгоритм аппроксимации который выводит не более ак медианы со стоимостью не более б умноженное на оптимальное k-медианное решение, и на шаге 4 мы запускаем c-приближенного алгоритма, то коэффициент аппроксимации алгоритма Small-Space () равен . Мы также можем обобщить Small-Space, чтобы он рекурсивно называл себя я раз на последовательно уменьшающемся наборе взвешенных центров и достигает приближения постоянного множителя к k-средняя проблема.
Проблема с Small-Space заключается в том, что количество подмножеств что мы разделяем S в ограничен, так как он должен хранить в памяти промежуточные медианы в Икс. Так что если M это размер памяти, нам нужно разбить S в такие подмножества, что каждое подмножество умещается в памяти, (), так что взвешенные центры тоже помещаются в памяти, . Но такой может не всегда существовать.
Алгоритм STREAM решает проблему хранения промежуточных медиан и обеспечивает лучшее время выполнения и требования к пространству. Алгоритм работает следующим образом:[3]
- Введите первый м точки; используя рандомизированный алгоритм, представленный в[3] уменьшить их до (скажем, 2k) точки.
- Повторяйте вышеизложенное, пока не увидим м2/(2k) исходных точек данных. Теперь у нас есть м промежуточные медианы.
- Используя местный поиск алгоритм, сгруппируйте эти м медианы первого уровня на 2k медианы второго уровня и продолжаем.
- В общем, поддерживайте не более м уровень-я медианы, и, увидев м, сгенерировать 2k уровень-я+ 1 медианы, где вес новой медианы как сумма весов промежуточных медиан, присвоенных ей.
- Когда мы увидим все исходные точки данных, мы сгруппируем все промежуточные медианы в k конечные медианы с использованием первичного двойственного алгоритма.[4]
Другие алгоритмы
Другие известные алгоритмы, используемые для кластеризации потока данных:
- БЕРЕЗА:[5] строит иерархическую структуру данных для постепенной кластеризации входящих точек с использованием доступной памяти и минимизации требуемого количества операций ввода-вывода. Сложность алгоритма составляет поскольку для получения хорошей кластеризации достаточно одного прохода (хотя результаты можно улучшить, разрешив несколько проходов).
- COBWEB:[6][7] метод инкрементальной кластеризации, который сохраняет иерархическая кластеризация модель в виде дерево классификации. Для каждой новой точки COBWEB спускается по дереву, обновляет узлы по пути и ищет лучший узел, на который можно поставить точку (используя функция полезности категории ).
- C2ICM:[8] строит структуру кластеризации с плоским секционированием, выбирая некоторые объекты в качестве начальных значений / инициаторов кластера, и не-начальное значение назначается начальному значению, которое обеспечивает максимальное покрытие, добавление новых объектов может ввести новые начальные значения и фальсифицировать некоторые существующие старые начальные числа во время инкрементальной кластеризации новых объекты и члены фальсифицированных кластеров назначаются одному из существующих новых / старых семян.
- CluStream:[9] использует микрокластеры, которые являются временными расширениями БЕРЕЗА [5] вектор признаков кластера, чтобы он мог решить, можно ли создать новый, объединить или забыть микрокластер, на основе анализа квадрата и линейной суммы текущих точек данных и временных меток микрокластеров, а затем в любой момент раз можно создать макрокластеры путем кластеризации этих микрокластеров с использованием автономного алгоритма кластеризации, такого как К-средние, что дает окончательный результат кластеризации.
Рекомендации
- ^ Munro, J .; Патерсон, М. (1980). «Отбор и сортировка при ограниченном хранилище». Теоретическая информатика. 12 (3): 315–323. Дои:10.1016/0304-3975(80)90061-4.
- ^ Henzinger, M .; Raghavan, P .; Раджагопалан, С. (август 1998 г.). «Вычисления на потоках данных». Корпорация цифрового оборудования. TR-1998-011. CiteSeerX 10.1.1.19.9554.
- ^ а б c Guha, S .; Mishra, N .; Motwani, R .; О'Каллаган, Л. (2000). «Кластеризация потоков данных». Материалы ежегодного симпозиума по основам компьютерных наук: 359–366. CiteSeerX 10.1.1.32.1927. Дои:10.1109 / SFCS.2000.892124. ISBN 0-7695-0850-2.
- ^ Jain, K .; Вазирани, В. (1999). Алгоритмы первично-дуальной аппроксимации для метрического размещения объектов и задач k-медианы. Proc. FOCS. Focs '99. С. 2–. ISBN 9780769504094.
- ^ а б Zhang, T .; Ramakrishnan, R .; Линви, М. (1996). «БЕРЕЗА: эффективный метод кластеризации данных для очень больших баз данных». Материалы конференции ACM SIGMOD по управлению данными. 25 (2): 103–114. Дои:10.1145/235968.233324.
- ^ Фишер, Д. Х. (1987). «Приобретение знаний посредством инкрементальной концептуальной кластеризации». Машинное обучение. 2 (2): 139–172. Дои:10.1023 / А: 1022852608280.
- ^ Фишер, Д. Х. (1996). «Итерационная оптимизация и упрощение иерархических кластеров». Журнал исследований ИИ. 4. arXiv:cs / 9604103. Bibcode:1996cs ........ 4103F. CiteSeerX 10.1.1.6.9914.
- ^ Джан, Ф. (1993). «Инкрементальная кластеризация для динамической обработки информации». ACM-транзакции в информационных системах. 11 (2): 143–164. Дои:10.1145/130226.134466.
- ^ Aggarwal, Charu C .; Yu, Philip S .; Хан, Цзявэй; Ван, Цзяньюн (2003). «Платформа для кластеризации развивающихся потоков данных» (PDF). Труды 2003 VLDB Conference: 81–92. Дои:10.1016 / B978-012722442-8 / 50016-1.











