Вейвлет Добеши - Daubechies wavelet

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: "Вейвлет Добеши"  – Новости  · газеты  · книги  · ученый  · JSTOR (Август 2009 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Двухмерный вейвлет Добеши 20 (Вейвлет Fn X Scaling Fn)

В Вейвлеты Добеши, основанный на работе Ингрид Добеши, семья ортогональные вейвлеты определение дискретное вейвлет-преобразование и характеризуется максимальным числом исчезающих моменты для некоторых данных поддерживать. Для каждого типа вейвлета этого класса существует функция масштабирования (называемая отец вейвлет), который порождает ортогональный многокомпонентный анализ.

Характеристики

Обычно вейвлеты Добеши выбираются так, чтобы иметь наибольшее число А исчезающих моментов (это не означает лучшей гладкости) для заданной ширины опоры (числа коэффициентов) 2А.^[1] Используются две схемы именования: DN используя длину или количество ответвлений, а dbА имея в виду количество исчезающих моментов. Итак, D4 и db2 - это одно и то же вейвлет-преобразование.

Среди 2^А−1 возможных решений алгебраических уравнений для момента и условий ортогональности, выбирается то, масштабный фильтр которого имеет экстремальную фазу. Вейвлет-преобразование также легко реализовать на практике, используя быстрое вейвлет-преобразование. Вейвлеты Добеши широко используются для решения широкого круга задач, например свойства самоподобия сигнала или фрактал проблемы, прерывания сигнала и т. д.

Вейвлеты Добеши не определены в терминах результирующих функций масштабирования и вейвлетов; фактически их невозможно записать в закрытая форма. Графики ниже построены с использованием каскадный алгоритм, числовой метод, состоящий из обратного преобразования [1 0 0 0 0 ...] подходящее количество раз.

Масштабирование и вейвлет-функции
Амплитуды частотных спектров указанных функций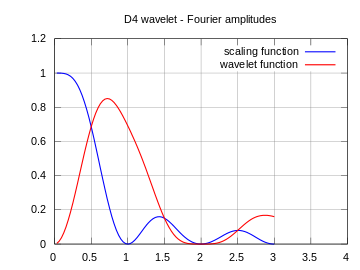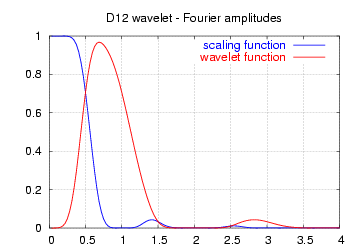

Обратите внимание, что представленные здесь спектры не являются частотными характеристиками фильтров высоких и низких частот, а скорее амплитудами непрерывных преобразований Фурье функций масштабирования (синий) и вейвлета (красный).

Ортогональные вейвлеты Добеши D2 – D20 соотв. Обычно используются db1 – db10. Номер индекса относится к числу N коэффициентов. Каждый вейвлет имеет несколько нулевые моменты или же исчезающие моменты равняется половине числа коэффициентов. Например, у D2 один момент исчезновения, у D4 два и т. Д. Уходящий момент ограничивает способность вейвлетов представлять многочлен поведение или информация в сигнале. Например, D2 с одним нулевым моментом легко кодирует полиномы одного коэффициента или постоянные компоненты сигнала. D4 кодирует полиномы с двумя коэффициентами, то есть постоянной и линейной составляющими сигнала; а D6 кодирует 3-полиномы, то есть постоянные, линейные и квадратичный компоненты сигнала. Эта способность кодировать сигналы, тем не менее, зависит от феномена утечка накипи, а также отсутствие инвариантности к сдвигу, которые возникают из-за операции дискретного сдвига (см. ниже) во время применения преобразования. Подпоследовательности, которые представляют линейные, квадратичный (например) компоненты сигнала обрабатываются преобразованием по-разному в зависимости от того, совпадают ли точки с точками с четными или нечетными номерами в последовательности. Отсутствие важного свойства инвариантность к сдвигу, привело к разработке нескольких различных версий инвариантное к сдвигу (дискретное) вейвлет-преобразование.

Строительство

Эта секция может быть сбивает с толку или неясно читателям. В частности, есть неопределенные математические символы (например, a, p, P). Пожалуйста, помоги нам прояснить раздел. Возможно обсуждение этого вопроса на страница обсуждения. (Сентябрь 2019) (Узнайте, как и когда удалить этот шаблон сообщения)

Как последовательность масштабирования (фильтр нижних частот), так и последовательность вейвлетов (полосовой фильтр) (см. ортогональный вейвлет для деталей этой конструкции) здесь будет нормализована, чтобы иметь сумму, равную 2, и сумму квадратов, равную 2. В некоторых приложениях они нормализованы, чтобы иметь сумму ${ displaystyle { sqrt {2}}}$, так что обе последовательности и все их сдвиги на четное число коэффициентов ортонормированы друг другу.

Используя общее представление масштабной последовательности ортогонального дискретного вейвлет-преобразования с порядком аппроксимации А,

${ Displaystyle а (Z) = 2 ^ {1-A} (1 + Z) ^ {A} p (Z),}$

с N = 2А, п с действительными коэффициентами, п(1) = 1 и deg (п) = А - 1 условие ортогональности можно записать в виде

${ Displaystyle а (Z) а влево (Z ^ {- 1} вправо) + а (-Z) а влево (-Z ^ {- 1} вправо) = 4,}$

или равно как

${ Displaystyle (2-X) ^ {A} P (X) + X ^ {A} P (2-X) = 2 ^ {A} qquad (*),}$

с полиномом Лорана

${ displaystyle X: = { frac {1} {2}} left (2-Z-Z ^ {- 1} right)}$

генерируя все симметричные последовательности и ${ Displaystyle X (-Z) = 2-X (Z).}$ Дальше, п(Икс) обозначает симметричный полином Лорана

${ Displaystyle P (X (Z)) = p (Z) p left (Z ^ {- 1} right).}$

С

${ Displaystyle Х (е ^ {iw}) = 1- соз (ш)}$

${ displaystyle p (e ^ {iw}) p (e ^ {- iw}) = | p (e ^ {iw}) | ^ {2}}$

п принимает неотрицательные значения на отрезке [0,2].

Уравнение (*) имеет одно минимальное решение для каждого А, который можно получить делением в кольцо усеченных степенных рядов по Икс,

${ Displaystyle P_ {A} (X) = sum _ {k = 0} ^ {A-1} { binom {A + k-1} {A-1}} 2 ^ {- k} X ^ { k}.}$

Очевидно, это имеет положительные значения на (0,2).

Однородное уравнение для (*) антисимметрично относительно Икс = 1 и, таким образом, имеет общее решение

${ Displaystyle X ^ {A} (X-1) R влево ((X-1) ^ {2} right),}$

с р некоторый многочлен с действительными коэффициентами. Эта сумма

${ Displaystyle P (X) = P_ {A} (X) + X ^ {A} (X-1) R left ((X-1) ^ {2} right)}$

неотрицательна на интервале [0,2] переводится в набор линейных ограничений на коэффициенты р. Ценности п на отрезке [0,2] ограничены некоторой величиной ${ displaystyle 4 ^ {A-r},}$ максимизация р приводит к линейной программе с бесконечным числом условий неравенства.

Решать

${ Displaystyle Р (Икс (Z)) = п (Z) р влево (Z ^ {- 1} вправо)}$

за п один использует метод, называемый спектральной факторизацией, соответственно. Алгоритм Фейера-Рисса. Полином п(Икс) разбивается на линейные множители

${ Displaystyle P (X) = (X- mu _ {1}) cdots (X- mu _ {N}), qquad N = A + 1 + 2 deg (R).}$

Каждый линейный множитель представляет собой полином Лорана

${ Displaystyle X (Z) - mu = - { frac {1} {2}} Z + 1- mu - { frac {1} {2}} Z ^ {- 1}}$

это можно разложить на два линейных фактора. Можно присвоить любой из двух линейных факторов п(Z), поэтому получаем 2^N возможные решения. Для экстремальной фазы выбирается та, которая имеет все комплексные корни из п(Z) внутри или на единичном круге и, таким образом, является реальным.

Для вейвлет-преобразования Добеши используется пара линейных фильтров. Эта пара фильтров должна иметь свойство, называемое квадратурным зеркальным фильтром. Решение коэффициента линейного фильтра ${ displaystyle c_ {i}}$ Использование свойства квадратурного зеркального фильтра приводит к приведенному ниже решению для значений коэффициентов для фильтра порядка 4.

${ displaystyle c_ {0} = { frac {1 + { sqrt {3}}} {4 { sqrt {2}}}}, quad c_ {1} = { frac {3 + { sqrt) {3}}} {4 { sqrt {2}}}}, quad c_ {2} = { frac {3 - { sqrt {3}}} {4 { sqrt {2}}}}, quad c_ {3} = { frac {1 - { sqrt {3}}} {4 { sqrt {2}}}}.}$

Масштабирующие последовательности низшего порядка аппроксимации

Ниже приведены коэффициенты масштабных функций для D2-20. Вейвлет-коэффициенты получаются путем изменения порядка функция масштабирования коэффициенты, а затем меняют знак каждого второго (то есть вейвлет D4 ${ Displaystyle приблизительно}$ {-0,1830127, -0,3169873, 1,1830127, -0,6830127}). Математически это выглядит как ${ displaystyle b_ {k} = (- 1) ^ {k} a_ {N-1-k}}$ куда k - индекс коэффициента, б - коэффициент вейвлет-последовательности и а коэффициент масштабирующей последовательности. N - индекс вейвлета, т.е. 2 для D2.

Части конструкции также используются для получения биортогонального Вейвлеты Коэна – Добеши – Фово (CDF).

Выполнение

В то время как программное обеспечение, такое как Mathematica поддерживает вейвлеты Добеши напрямую^[2] базовая реализация возможна в MATLAB (в данном случае Добеши 4). Эта реализация использует периодизацию для решения проблемы сигналов конечной длины. Доступны и другие, более сложные методы, но часто в них нет необходимости, поскольку они влияют только на самые концы преобразованного сигнала. Периодизация выполняется в прямом преобразовании непосредственно в векторной нотации MATLAB, а обратное преобразование - с использованием circshift () функция:

Преобразование, D4

Предполагается, что Sвектор-столбец с четным числом элементов был предварительно определен как сигнал для анализа. Обратите внимание, что коэффициенты D4 равны [1 +√3, 3 + √3, 3 − √3, 1 − √3]/4.

N = длина(S);s1 = S(1:2:N - 1) + sqrt(3) * S(2:2:N);d1 = S(2:2:N) - sqrt(3) / 4 * s1 - (sqrt(3) - 2) / 4 * [s1(N / 2); s1(1:N / 2 - 1)];s2 = s1 - [d1(2:N / 2); d1(1)];s = (sqrt(3) - 1) / sqrt(2) * s2;d = - (sqrt(3) + 1) / sqrt(2) * d1;

Обратное преобразование, D4

d1 = d * ((sqrt(3) - 1) / sqrt(2));s2 = s * ((sqrt(3) + 1) / sqrt(2));s1 = s2 + круговой сдвиг(d1, - 1);S(2:2:N) = d1 + sqrt(3) / 4 * s1 + (sqrt(3) - 2) / 4 * круговой сдвиг(s1, 1);S(1:2:N - 1) = s1 - sqrt(3) * S(2:2:N);

Смотрите также

• Биномиальный-QMF (Вейвлет-фильтры Добеши)
• Быстрое вейвлет-преобразование

Рекомендации

• Дженсен; ла Кур-Харбо (2001). Рябь в математике. Берлин: Springer. С. 157–160. ISBN  3-540-41662-5.

• Цзяньхун (Джеки) Шен и Гилберт Стрэнг, Прикладной и вычислительный гармонический анализ, 5(3), Асимптотика фильтров Добеши, функций масштабирования и всплесков.

внешняя ссылка

• Ингрид Добешис: Десять лекций по вейвлетам, SIAM 1992
• А.Н. Акансу, Эффективная структура QMF-вейвлета (Биномиальные QMF всплески Добеши), Proc. 1-й симпозиум NJIT по вейвлетам, апрель 1990 г.
• Proc. 1-й симпозиум NJIT по вейвлетам, поддиапазонам и преобразованиям, апрель 1990 г.
• А.Н. Акансу, Р.А. Хаддад и Х. Каглар, Биномиальное QMF-вейвлет-преобразование с идеальной реконструкцией, Proc. SPIE Визуальные коммуникации и обработка изображений, стр. 609–618, Лозанна, сентябрь 1990 г.
• Карлос Кабрелли, Урсула Молтер: Обобщенное самоподобие », Журнал математического анализа и приложений, 230: 251–260, 1999.
• Аппаратная реализация вейвлетов
• "Вейвлеты Добеши", Энциклопедия математики, EMS Press, 2001 [1994]
• И. Каплан, Вейвлет-преобразование Добеши D4.