Азартные игры и теория информации - Gambling and information theory
Статистические выводы можно рассматривать как теорию азартных игр, применимую к окружающему нас миру. Множество приложений для логарифмические информационные меры расскажите нам, как сделать наилучшее предположение в условиях неполной информации.[1] В этом смысле, теория информации можно рассматривать как формальное выражение теории азартных игр. Поэтому неудивительно, что теория информации имеет приложения к азартным играм.[2]
Келли Беттинг
Ставки Келли или пропорциональные ставки - это применение теория информации к инвестирование и играть в азартные игры. Его первооткрывателем был Джон Ларри Келли младший.
Часть идеи Келли состояла в том, чтобы заставить игрока максимизировать ожидание выигрыша. логарифм его капитала, а не ожидаемой прибыли от каждой ставки. Это важно, так как в последнем случае человек будет вынужден поставить все, что у него есть, когда ему будет предложена выгодная ставка, а если он проиграет, у него не будет капитала для последующих ставок. Келли понял, что это логарифм капитала игрока, который складывается в последовательных ставках и «к которому применяется закон больших чисел».
Дополнительная информация
А кусочек это количество энтропия в событии с таблицей ставок с двумя возможными исходами и равными коэффициентами. Очевидно, мы могли бы удвоить наши деньги, если бы знали заранее, каков будет исход этого события. Келли пришел к выводу, что независимо от того, насколько сложен сценарий ставок, мы можем использовать оптимальную стратегию ставок, называемую Критерий Келли, чтобы наши деньги росли экспоненциально с любой дополнительной информацией, которую мы можем получить. Ценность этой "незаконной" дополнительной информации измеряется как взаимная информация относительно исхода события, на которое можно сделать ставку:
куда Y это дополнительная информация, Икс является результатом события, на которое можно сделать ставку, и я уровень информированности букмекерской конторы. Это средний Дивергенция Кульбака – Лейблера или получение информации апостериорный распределение вероятностей Икс учитывая ценность Y относительно априори распределение или заявленные шансы на Икс. Обратите внимание, что ожидание превзошло Y скорее, чем Икс: нам нужно оценить, насколько точна в долгосрочной перспективе наша дополнительная информация Y до того, как мы начнем делать ставки на реальные деньги Икс. Это прямое применение Байесовский вывод. Обратите внимание, что дополнительная информация Y может повлиять не только на наши знания о мероприятии Икс но и само мероприятие. Например, Y может быть лошадь, у которой слишком много овса или недостаточно воды. Та же самая математика применима и в этом случае, потому что с точки зрения букмекера, случайные фиксации гонок уже учитываются, когда он рассчитывает свои коэффициенты.
Дополнительная информация чрезвычайно привередлива. Мы уже видели, что это может повлиять на фактическое событие, а также на наши знания о результате. Предположим, у нас есть информатор, который сообщает нам, что определенная лошадь собирается победить. Мы, конечно, не хотим ставить все наши деньги на эту лошадь только на слух: этот информатор может делать ставку на другую лошадь и, возможно, распространяет слухи только для того, чтобы самому получить лучшие шансы. Вместо этого, как мы указали, нам необходимо оценить нашу дополнительную информацию в долгосрочной перспективе, чтобы увидеть, как она соотносится с результатами гонок. Таким образом, мы можем точно определить, насколько надежен наш информатор, и сделать ставки именно так, чтобы максимизировать ожидаемый логарифм нашего капитала в соответствии с критерием Келли. Даже если наш информатор лжет нам, мы все равно можем извлечь выгоду из его лжи, если сможем найти некоторую обратную корреляцию между его подсказками и реальными результатами гонки.
Удвоение скорости
Удвоение ставки в азартных играх на скачки является [3]
где есть лошадей, вероятность -я лошадь-победитель , доля богатства, поставленная на лошадь, , а шансы (выплата) быть (например., если При выигрыше лошади выплачивается двойная ставка). Это количество максимизируется пропорциональной игрой (Келли):
для которого
куда является информационная энтропия.
Ожидаемая прибыль
Между количеством дополнительной информации, которую получает игрок, и ожидаемым экспоненциальным ростом его капитала (Келли) существует важная, но простая связь:
для оптимальной стратегии ставок, где - начальный капитал, столица после тй ставку, и количество дополнительной информации, полученной относительно яй ставку (в частности, взаимная информация относительно исхода каждого события, на которое можно сделать ставку). Это уравнение применяется при отсутствии каких-либо транзакционных издержек или минимальных ставок. Когда применяются эти ограничения (как это всегда происходит в реальной жизни), в игру вступает еще одна важная концепция азартных игр: игрок (или недобросовестный инвестор) должен столкнуться с определенной вероятностью окончательного разорения, которая известна как разорение игрока сценарий. Обратите внимание, что даже еда, одежда и жилье могут считаться фиксированными операционными издержками и, таким образом, увеличивать вероятность окончательного разорения игрока.
Это уравнение было первым применением теории информации Шеннона за рамками преобладающей парадигмы передачи данных (Пирс).
Приложения для самоинформации
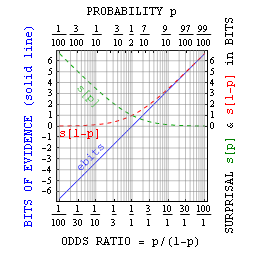
Логарифмическая вероятностная мера самоинформация или сюрприз,[4] чья средняя информационная энтропия / неопределенность и средняя разность KL-дивергенция, сама по себе имеет приложения для анализа шансов. Его две основные сильные стороны заключаются в том, что они неожиданны: (i) уменьшают мизерные вероятности до числа управляемого размера и (ii) добавляют всякий раз, когда вероятности умножаются.
Например, можно сказать, что «количество состояний равно двум количеству битов», т.е. #states = 2#bits. Здесь величина, которая измеряется в битах, является упомянутой выше логарифмической мерой информации. Следовательно, выпадение всех орлов при первом броске из N монет вызывает N неожиданностей.
Аддитивный характер сюрпризов и способность почувствовать их значение с помощью горстки монет могут помочь поместить невероятные события (например, выигрыш в лотерею или несчастный случай) в контекст. Например, если выигрывает один из 17 миллионов билетов, то неожиданность выигрыша от одного случайного выбора составляет около 24 бит. Несколько раз бросив 24 монеты, вы почувствуете сюрприз, когда все решится с первой попытки.
Аддитивный характер этой меры также пригодится при взвешивании альтернатив. Например, представьте, что вред от вакцинации составляет 20 бит. Если неожиданность выявления болезни без вакцинации составляет 16 бит, но неожиданность вреда от болезни, если вы ее поймаете, составляет 2 бита, тогда неожиданность вреда от НЕ получения вакцинации составляет всего 16 + 2 = 18 бит. Независимо от того, решите вы пройти вакцинацию или нет (например, денежные затраты на ее оплату не включены в это обсуждение), вы можете, по крайней мере, принять на себя ответственность за решение, основанное на том, что отказ от вакцинации требует большего, чем немного дополнительного риска.
В более общем плане вероятность p можно связать с кусочками неожиданности. сбиты как вероятность = 1/2сбиты. Как было предложено выше, это в основном полезно с малыми вероятностями. Однако Джейнс указал, что с помощью утверждений истина-ложь можно также определить фрагменты доказательства. ebits как сюрприз против минус сюрприза за. Это свидетельство в битах просто связано с отношением шансов = p / (1-p) = 2.ebits, и имеет преимущества, аналогичные преимуществам самоинформации.
Приложения в азартных играх
Теорию информации можно рассматривать как способ количественной оценки информации для принятия наилучшего решения перед лицом несовершенной информации. То есть как принять наилучшее решение, используя только имеющуюся у вас информацию. Смысл ставок состоит в том, чтобы рационально оценить все соответствующие переменные неопределенной игры / расы / матча, затем сравнить их с оценками букмекерской конторы, которые обычно представлены в форме коэффициентов или спредов, и сделать правильную ставку, если оценки существенно различаются.[5] Сфера азартных игр, где это используется больше всего, - это ставки на спорт. Спортивная инвалидность очень хорошо поддается теории информации из-за доступности статистики. В течение многих лет известные экономисты проверяли различные математические теории, используя спорт в качестве лаборатории, с очень разными результатами.
Одна из теорий относительно ставок на спорт состоит в том, что это случайная прогулка. Случайное блуждание - это сценарий, при котором новая информация, цены и доходность будут колебаться случайно, это часть гипотезы эффективного рынка. Основополагающее убеждение в гипотезе эффективного рынка заключается в том, что рынок всегда будет вносить поправки в любую новую информацию. Следовательно, никто не может превзойти рынок, потому что он торгует на той же информации, на основании которой рынок корректировался. Однако, по словам Фамы,[6] Для создания эффективного рынка необходимо соблюдение трех качеств:
- При торговле ценными бумагами отсутствуют транзакционные издержки.
- Вся доступная информация бесплатно доступна всем участникам рынка.
- Все согласны с последствиями текущей информации для текущей цены и распределения будущих цен каждой ценной бумаги.
Статистики показали, что это третье условие, которое позволяет теории информации быть полезной в борьбе с физическими недостатками в спорте. Когда все не согласны с тем, как информация повлияет на исход события, мы получаем разные мнения.
Смотрите также
Рекомендации
- ^ Джейнс, Э. (1998/2003) Теория вероятностей: логика науки (Cambridge U. Press, Нью-Йорк).
- ^ Келли, Дж. Л. (1956). «Новая интерпретация скорости информации» (PDF). Технический журнал Bell System. 35 (4): 917–926. Дои:10.1002 / j.1538-7305.1956.tb03809.x.
- ^ Томас М. Обложка, Джой А. Томас. Элементы теории информации, 1-е издание. Нью-Йорк: Wiley-Interscience, 1991. ISBN 0-471-06259-6, Глава 6.
- ^ Трибус, Майрон (1961) Термодинамика и термостатика: введение в энергию, информацию и состояния материи с инженерными приложениями (D. Van Nostrand Company Inc., 24 West 40 Street, New York 18, New York, USA) ASIN: B000ARSH5S.
- ^ Хансен, Кристен Бринч. (2006) Ставки на спорт с точки зрения поведенческих финансов (Орхусская школа бизнеса).
- ^ Фама, Э.Ф. (1970) "Эффективные рынки капитала: обзор теории и независимой работы", Журнал финансовой экономики Том 25, 383-417


![{displaystyle W (b, p) = mathbb {E} [log _ {2} S (X)] = sum _ {i = 1} ^ {m} p_ {i} log _ {2} b_ {i} o_ {я}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7709e5610bd7a212201e0e6ff5219ed4468515bd)












