Геометрическое хеширование - Википедия - Geometric hashing

В Информатика, геометрическое хеширование - это метод эффективного поиска двумерных объектов, представленных дискретными точками, которые подверглись аффинное преобразование, хотя существуют расширения для других представлений и преобразований объектов. В автономном режиме объекты кодируются путем обработки каждой пары точек как геометрического объекта. основа. Остальные точки можно представить в виде инвариантный мода относительно этой основы с использованием двух параметров. Для каждой точки свой квантованный преобразованные координаты сохраняются в хеш-таблица как ключ, а индексы базисных точек как значение. Затем выбирается новая пара базисных точек, и процесс повторяется. На этапе онлайн (распознавания) случайно выбранные пары точек данных рассматриваются как базы-кандидаты. Для каждой основы-кандидата оставшиеся точки данных кодируются в соответствии с основанием, и возможные соответствия объекта находятся в ранее созданной таблице. Основа-кандидат принимается, если достаточно большое количество точек данных указывает на непротиворечивую основу объекта.

Первоначально геометрическое хеширование было предложено в компьютерное зрение за распознавание объекта в 2D и 3D,^[1] но позже был применен к различным задачам, таким как структурное выравнивание из белки.^[2]^[3]

Геометрическое хеширование в компьютерном зрении

Геометрическое хеширование - это метод, используемый для распознавания объектов. Допустим, мы хотим проверить, можно ли увидеть изображение модели во входном изображении. Этого можно добиться с помощью геометрического хеширования. Этот метод может использоваться для распознавания одного из нескольких объектов в базе, в этом случае хеш-таблица должна хранить не только информацию о позе, но и индекс объектной модели в базе.

Пример

Для простоты в этом примере не будет использоваться слишком много точечные особенности и предположим, что их дескрипторы заданы только их координатами (на практике локальные дескрипторы Такие как ПРОСЕЯТЬ может использоваться для индексации).

Фаза обучения

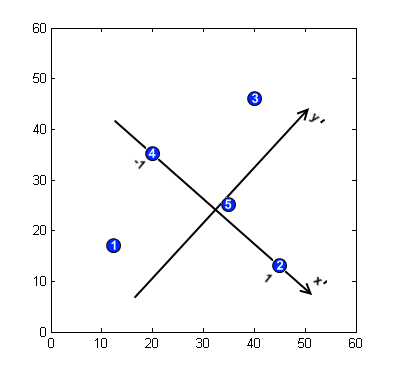
Точки объекта в системе координат изображения и оси для системы координат за основу (P2, P4)

Найдите характерные черты модели. Предположим, что на изображении модели обнаружены 5 характерных точек с координатами ${ Displaystyle (12,17);}$ ${ Displaystyle (45,13);}$ ${ displaystyle (40,46);}$ ${ displaystyle (20,35);}$ ${ displaystyle (35,25)}$ , смотрите картинку.
Введите основу для описания расположения характерных точек. Для 2D-пространства и преобразование подобия базис определяется парой точек. Исходная точка находится в середине отрезка, соединяющего две точки (P2, P4 в нашем примере), ${ displaystyle x '}$ ось направлена к одному из них, ${ displaystyle y '}$ ортогонален и проходит через начало координат. Масштаб выбран таким, чтобы абсолютное значение ${ displaystyle x '}$ для обеих базисных точек равно 1.
Опишите расположение пространственных объектов относительно этого базиса, то есть вычислите проекции на новые оси координат. Координаты должны быть дискретизированы для распознавания крепкий к шуму берем размер бина 0,25. Таким образом, мы получаем координаты ${ displaystyle (-0,75, -1,25);}$ ${ displaystyle (1.00,0.00);}$ ${ displaystyle (-0,50,1,25);}$ ${ displaystyle (-1.00,0.00);}$ ${ displaystyle (0,00,0,25)}$
Храните основу в хеш-таблица индексируется по объектам (в данном случае только преобразованные координаты). Если бы было больше объектов для сопоставления, мы также должны сохранить номер объекта вместе с базовой парой.
Повторите процесс для другой пары базисов (шаг 2). Это необходимо для обработки окклюзии. В идеале все не-коллинеарный пары должны быть пронумерованы. Предоставляем хеш-таблицу после двух итераций, для второй выбирается пара (P1, P3).

Хеш-таблица:

Вектор ( ${ displaystyle x '}$ , ${ displaystyle y '}$ )	основа
${ displaystyle (-0,75, -1,25);}$	(P2, P4)
${ displaystyle (1.00,0.00);}$	(P2, P4)
${ displaystyle (-0,50,1,25);}$	(P2, P4)
${ displaystyle (-1.00,0.00);}$	(P2, P4)
${ displaystyle (0,00,0,25)}$	(P2, P4)
${ displaystyle (1.00,0.00);}$	(P1, P3)
${ displaystyle (0.00,1.25);}$	(P1, P3)
${ displaystyle (-1.00,0.00);}$	(P1, P3)
${ displaystyle (0,00, -0,25);}$	(P1, P3)
${ displaystyle (0,00,0,50)}$	(P1, P3)

В большинстве хеш-таблиц не может быть одинаковых ключей, сопоставленных с разными значениями. Таким образом, в реальной жизни нельзя кодировать базовые ключи (1.0, 0.0) и (-1.0, 0.0) в хеш-таблице.

Фаза признания

Найдите интересные особенности во входном изображении.
Выбираем произвольную основу. Если подходящей произвольной основы нет, то вполне вероятно, что входное изображение не содержит целевой объект.
Опишите координаты характерных точек в новом базисе. Квантовать полученные координаты, как это делалось ранее.
Сравните все преобразованные точечные объекты на входном изображении с хеш-таблицей. Если точечные объекты идентичны или похожи, увеличьте счетчик для соответствующего базиса (и типа объекта, если таковой имеется).
Для каждого базиса, в котором счет превышает определенный порог, проверьте гипотезу о том, что он соответствует базису изображения, выбранному на шаге 2. Перенесите систему координат изображения в модельную (для предполагаемого объекта) и попытайтесь сопоставить их. В случае успеха объект найден. В противном случае вернитесь к шагу 2.

Поиск зеркального рисунка

Похоже, что этот метод может обрабатывать только масштабирование, перемещение и вращение. Однако входное изображение может содержать объект в зеркальном преобразовании. Следовательно, геометрическое хеширование также должно иметь возможность найти объект. Есть два способа обнаружить зеркальные объекты.

Для векторного графика сделайте левую часть положительной, а правую - отрицательной. Умножение позиции x на -1 даст тот же результат.
Используйте 3 точки за основу. Это позволяет обнаруживать зеркальные изображения (или объекты). Собственно, использование трех точек за основу - это еще один подход к геометрическому хешированию.

Геометрическое хеширование в более высоких измерениях

Как и в примере выше, хеширование применяется к многомерным данным. Для трехмерных точек данных также необходимы три точки в качестве основы. Первые две точки определяют ось x, а третья точка определяет ось y (с первой точкой). Ось z перпендикулярна созданной оси с использованием правила правой руки. Обратите внимание, что порядок точек влияет на итоговую основу

Смотрите также

Перцептивное хеширование