Сети взаимодействия - Interaction nets

Сети взаимодействия являются графическим модель вычисления разработан Ив Лафон в 1990 году^[1] как обобщение структур доказательства линейная логика. Система сети взаимодействия определяется набором типов агентов и набором правил взаимодействия. Сети взаимодействия по своей сути являются распределенной моделью вычислений в том смысле, что вычисления могут выполняться одновременно во многих частях сети взаимодействия, и синхронизация не требуется. Последнее гарантируется свойством сильного слияния редукции в этой модели вычислений. Таким образом, сети взаимодействия предоставляют естественный язык для массового параллелизма. Сети взаимодействия лежат в основе многих реализаций лямбда-исчисление, например, эффективная закрытая редукция^[2] и оптимальная в смысле Леви Lambdascope.^[3]

Определения

Сети взаимодействий представляют собой графоподобные структуры, состоящие из агенты и края.

Агент типа ${displaystyle alpha}$ и с арность ${displaystyle {ext {ar}} (альфа) = ngeq 0}$ есть один главный порт и ${displaystyle n}$ вспомогательные порты. Любой порт может быть подключен не более чем к одному краю. Порты, которые не связаны ни с одним ребром, называются свободные порты. Свободные порты вместе образуют интерфейс сети взаимодействия. Все типы агентов входят в набор ${displaystyle Sigma}$ называется подпись.

Сеть взаимодействия, состоящая исключительно из ребер, называется сетью взаимодействия. проводка и обычно обозначается как ${displaystyle omega}$ . А дерево ${displaystyle t}$ с этими корень ${displaystyle x}$ индуктивно определяется либо как ребро ${displaystyle x}$ , или как агент ${displaystyle alpha}$ со своим основным свободным портом ${displaystyle x}$ и его вспомогательные порты ${displaystyle x_ {i}}$ связаны с корнями других деревьев ${displaystyle t_ {i}}$ .

Графически примитивные структуры сетей взаимодействия можно представить следующим образом:

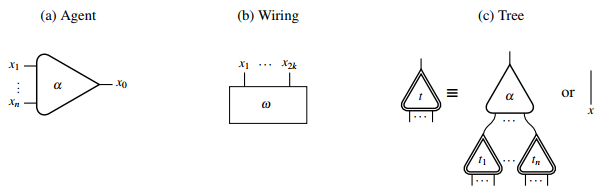
Примитивы сетей взаимодействия

Когда два агента соединяются друг с другом своими основными портами, они образуют активная пара. Фракционные пары можно ввести правила взаимодействия которые описывают, как активная пара перезаписывается в другую сеть взаимодействия. Сеть взаимодействия без активных пар называется нормальная форма. Подпись ${displaystyle Sigma}$ (с ${displaystyle {ext {ar}}: сигма ightarrow mathbb {N}}$ определены на нем) вместе с набором правил взаимодействия, определенных для агентов ${displaystyle alpha в Sigma}$ вместе составляют система взаимодействия.

Расчет взаимодействия

Текстовое представление сетей взаимодействия называется исчисление взаимодействий^[4] и его можно рассматривать как язык программирования.

Индуктивно определенные деревья соответствуют термины ${displaystyle t :: = alpha (t_ {1}, точки, t_ {n}) | Икс}$ в исчислении взаимодействий, где ${displaystyle x}$ называется имя.

Любая сеть взаимодействия ${displaystyle N}$ могут быть перерисованы с использованием ранее определенных примитивов проводки и дерева следующим образом:

Сеть взаимодействия как конфигурация

что в исчислении взаимодействий соответствует конфигурация

${displaystyle cequiv langle t_ {1}, dots, t_ {m} | v_ {1} = w_ {1}, точки, v_ {n} = w_ {n} угол}$ ,

куда ${displaystyle t_ {i}}$ , ${displaystyle v_ {i}}$ , и ${displaystyle w_ {i}}$ являются произвольными терминами. Упорядоченная последовательность ${displaystyle t_ {1}, ..., t_ {m}}$ в левой части называется интерфейс, а в правой части - неупорядоченное мультимножество уравнения ${displaystyle v_ {i} = w_ {i}}$ . Проводка ${displaystyle omega}$ переводится в имена, и каждое имя должно встречаться в конфигурации ровно дважды.

Как и в ${displaystyle lambda}$ -исчисление, исчисление взаимодействий имеет понятия ${displaystyle alpha}$ -конверсия и замена естественно определяется на конфигурациях. В частности, оба вхождения любого имени могут быть заменены новым именем, если последнее не встречается в данной конфигурации. Конфигурации считаются эквивалентными до ${displaystyle alpha}$ -конверсия. В свою очередь, замена ${displaystyle t [x: = u]}$ является результатом замены имени ${displaystyle x}$ в срок ${displaystyle t}$ с другим сроком ${displaystyle u}$ если ${displaystyle x}$ имеет ровно одно вхождение в термин ${displaystyle t}$ .

Любое правило взаимодействия можно графически представить следующим образом:

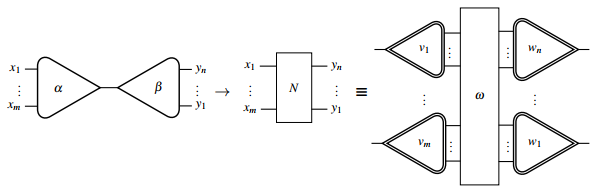
Правило взаимодействия

куда ${displaystyle alpha, eta в Sigma}$ , а сеть взаимодействия ${displaystyle N}$ в правой части перерисовывается с использованием примитивов проводки и дерева для преобразования в исчисление взаимодействий как ${displaystyle alpha [v_ {1}, dots, v_ {m}] owtie eta [w_ {1}, dots, w_ {n}]}$ используя обозначения Лафонта.

Исчисление взаимодействий определяет сокращение конфигураций более подробно, чем видно из графического написания, определенного для сетей взаимодействия. А именно, если ${displaystyle alpha [v_ {1}, dots, v_ {m}] owtie eta [w_ {1}, dots, w_ {n}]}$ , следующее сокращение:

${displaystyle langle {vec {t}} | альфа (t_ {1}, точки, t_ {m}) = eta (u_ {1}, точки, u_ {n}), Дельта-угол ightarrow langle {vec {t}} | t_ {1} = v_ {1}, точки, t_ {m} = v_ {m}, u_ {1} = w_ {1}, точки, u_ {n} = w_ {n}, угол дельты}$

называется взаимодействие. Когда одно из уравнений имеет вид ${displaystyle x = u}$ , косвенное обращение может применяться в результате замены другого вхождения имени ${displaystyle x}$ в какой-то срок ${displaystyle t}$ :

${displaystyle langle dots tdots | x = u, дельта-угол точки langle t [x: = u] точек | Дельта-угол}$ или же ${displaystyle langle {vec {t}} | x = u, t = w, дельта-угол ightarrow langle {vec {t}} | t [x: = u] = w, дельта-угол}$ .

Уравнение ${displaystyle x = t}$ называется тупик если ${displaystyle x}$ имеет возникновение в срок ${displaystyle t}$ . Обычно рассматриваются только сети взаимодействия без тупиков. Вместе взаимодействие и косвенность определяют отношение редукции в конфигурациях. Тот факт, что конфигурация ${displaystyle c}$ сводится к его нормальная форма ${displaystyle c '}$ без оставшихся уравнений обозначается как ${displaystyle cdownarrow c '}$ .

Характеристики

Сети взаимодействия обладают следующими свойствами:

местонахождение (перезаписывать можно только активные пары);
линейность (каждое правило взаимодействия может применяться в постоянное время);
сильное слияние также известное как свойство одношагового алмаза (если ${displaystyle cightarrow c_ {1}}$ и ${displaystyle cightarrow c_ {2}}$ , тогда ${displaystyle c_ {1} ightarrow c '}$ и ${displaystyle c_ {2} ightarrow c '}$ для некоторых ${displaystyle c '}$ ).

Вместе эти свойства обеспечивают массовый параллелизм.

Комбинаторы взаимодействия

Одна из простейших систем взаимодействия, которая может имитировать любую другую систему взаимодействия, - это система комбинаторы взаимодействия.^[5] Его подпись ${displaystyle Sigma = {epsilon, delta, gamma}}$ с ${displaystyle {ext {ar}} (epsilon) = 0}$ и ${displaystyle {ext {ar}} (delta) = {ext {ar}} (gamma) = 2}$ . Правила взаимодействия для этих агентов:

${displaystyle epsilon owtie alpha [эпсилон, точки, эпсилон]}$ называется стирание;
${displaystyle delta [alpha (x_ {1}, dots, x_ {n}), alpha (y_ {1}, dots, y_ {n})] owtie alpha [delta (x_ {1}, y_ {1}), точки, дельта (x_ {n}, y_ {n})]}$ называется дублирование;
${displaystyle delta [x, y] owtie delta [x, y]}$ и ${displaystyle gamma [x, y] owtie gamma [y, x]}$ называется уничтожение.

Графически правила стирания и дублирования можно представить следующим образом:

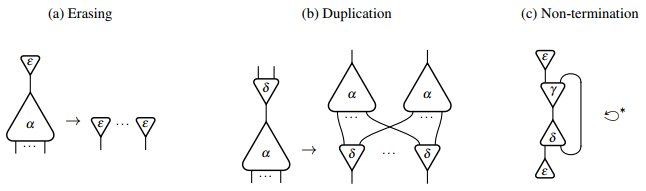
Примеры сетей взаимодействия

с примером непрерывной сети взаимодействия, которая сводится к самой себе. Его бесконечная последовательность редукций, начиная с соответствующей конфигурации в исчислении взаимодействий, выглядит следующим образом:

${displaystyle {egin {align} & langle varnothing | дельта (эпсилон, х) = гамма (х, эпсилон) угол ightarrow & langle varnothing | epsilon = гамма (x_ {1}, x_ {2}), x = gamma (y_ {1}, y_ {2}), x = delta (x_ {1}, y_ {1}), epsilon = delta (x_ {2}, y_ {2}) угол ightarrow ^ {*} & langle varnothing | x_ {1} = эпсилон, x_ {2} = эпсилон, x = гамма (y_ {1}, y_ {2}), x = дельта (x_ {1}, y_ {1}), x_ {2} = эпсилон , y_ {2} = угол эпсилона ightarrow ^ {*} & langle varnothing | дельта (эпсилон, х) = гамма (х, эпсилон) угол ightarrow точки конец {выровнено}}}$

Недетерминированное расширение

Сети взаимодействия по существу детерминированы и не могут напрямую моделировать недетерминированные вычисления. Чтобы выразить недетерминированный выбор, необходимо расширить сети взаимодействия. Фактически достаточно ввести всего один агент. ${displaystyle {ext {amb}}}$ ^[6] с двумя основными портами и следующими правилами взаимодействия:

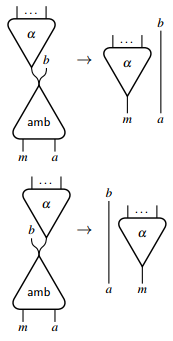
Недетерминированный агент

Этот выделенный агент представляет собой неоднозначный выбор и может использоваться для моделирования любого другого агента с произвольным количеством основных портов. Например, он позволяет определить ${displaystyle {ext {ParallelOr}}}$ логическая операция, которая возвращает истину, если любой из ее аргументов истинен, независимо от вычислений, выполняемых в других аргументах.

Смотрите также

дальнейшее чтение

Асперти, Андреа; Геррини, Стефано (1998). Оптимальная реализация языков функционального программирования. Кембриджские трактаты в теоретической информатике. 45. Издательство Кембриджского университета. ISBN 9780521621120.
Фернандес, Марибель (2009). «Модели вычислений, основанные на взаимодействии». Модели вычислений: введение в теорию вычислимости. Springer Science & Business Media. С. 107–130. ISBN 9781848824348.

внешняя ссылка

де Фалько, Марк. «тикз-инет. Набор макросов на основе тикз для рисования сетей взаимодействия».
де Фалько, Марк. "ИНЛ. Лаборатория сетей взаимодействия".
Виласа, Мигель. «INblobs. Редактор и интерпретатор для Interaction Nets».
Асперти, Андреа. «Болонская оптимальная машина высшего порядка».
Салихметов, Антон. "Двигатель JavaScript для интерактивных сетей".
Салихметов, Антон. «Макро-лямбда-исчисление».

[1] Лафон, Ив (1990). «Сети взаимодействия». Материалы 17-го симпозиума ACM SIGPLAN-SIGACT по принципам языков программирования. ACM: 95–108. Дои:10.1145/96709.96718. ISBN 0897913434.

[2] Маки, Ян (2008). «Реализация сети взаимодействия закрытого сокращения». Реализация и применение функциональных языков: 20-й международный симпозиум. Конспект лекций по информатике. 5836: 43–59. Дои:10.1007/978-3-642-24452-0_3. ISBN 978-3-642-24451-3.

[3] ван Остром, Винсент; ван де Лой, Кеес-Ян; Zwitserlood, Marijn (2010). «Лямбдаскоп: еще одна оптимальная реализация лямбда-исчисления» (PDF). Цитировать журнал требует | журнал = (помощь)

[4] Фернандес, Марибель; Маки, Ян (1999). «Расчет сетей взаимодействия». Принципы и практика декларативного программирования. Конспект лекций по информатике. Springer. 1702: 170–187. Дои:10.1007/10704567. ISBN 978-3-540-66540-3.

[5] Лафон, Ив (1997). «Комбинаторы взаимодействия». Информация и вычисления. Academic Press, Inc. 137 (1): 69–101. Дои:10.1006 / inco.1997.2643.

[6] Фернандес, Марибель; Халил, Лайонел (2003). «Сети взаимодействия с послом Маккарти: свойства и приложения». Северный вычислительный журнал. 10 (2): 134–162.

[1]

[2]

[3]

[4]

[5]

[6]