Хагаул - Khagaul
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
Хагаул Наинадхам | |
|---|---|
Город | |
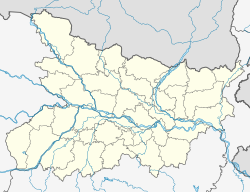 Хагаул Расположение в Бихаре, Индия | |
| Координаты: 25 ° 35'N 85 ° 03′E / 25,58 ° с. Ш. 85,05 ° в.Координаты: 25 ° 35'N 85 ° 03′E / 25,58 ° с. Ш. 85,05 ° в. | |
| Страна | |
| Состояние | Бихар |
| Округ | Патна |
| Площадь | |
| • Общий | 3 км2 (1 кв. Миль) |
| Высота | 55 м (180 футов) |
| численность населения (2011) | |
| • Общий | 44,364[1] |
| Языки | |
| • Официальный | Магахи, хинди |
| Часовой пояс | UTC + 5: 30 (IST ) |
| ШТЫРЬ | 801105 |
| Интернет сайт | Патна |
Хагаул это город и муниципалитет в Патна район в Индийский государственный из Бихар.
Обзор
Хагаул - город Нагар Паришад в районе Патна, Бихар. Город Хагаул разделен на 27 округов, выборы в которых проводятся каждые 5 лет.
В общей сложности Khagaul Nagar Parishad управляет 7 951 домом, который обеспечивает основные удобства, такие как вода и канализация. Он также имеет право строить дороги в пределах Нагар Паришад и взимать налоги с собственности, находящейся под его юрисдикцией.
География
Хагаул находится по адресу 25 ° 35'N 85 ° 03′E / 25,58 ° с. Ш. 85,05 ° в..[2] Его средняя высота составляет 55 метров (180 футов).
Демография
По состоянию на 2001 год[Обновить] Индия перепись,[1] Население Хагаула составляло 48 330 человек. Мужчины составляли 53% населения, а женщины 47%. Хагаул имел средний уровень грамотности 71,5%. В Хагауле 13% населения были моложе 6 лет.
По данным переписи населения Индии 2011 года[3]Население Khagaul Nagar Parishad составляло 44 364 человека, из которых 23 492 мужчины и 20 872 женщины.
Численность детей в возрасте от 0 до 6 лет составляет 5198 человек, что составляет 11,72% от общей численности населения Хагаула.
Соотношение женского пола составляет 888 против среднего показателя по штату 918.
Уровень грамотности в городе Хагаул на 86,82% выше, чем в среднем по штату 61,80%. В Хагауле уровень грамотности мужчин составляет около 91,81%, а уровень грамотности женщин - 81,23%.
История
Хагаул - историческое место. В древности, до нашей эры, Хагаул назывался Кусумпура или Кусумпур, недалеко от Паталипутры, столицы могущественной империи Магадх. Пушпапур находился между Паталипутрой и Кусумпуром. В наше время Паталипутра называется Патна, тогда как Кусумпура или Кусумпур называется Кхагаул, а Пушпапур называется Пхулвари или Пхулвари Шри или Пхулвари Шариф.
Шахтер и Чанакья (также известные как Каутилья или Вишнугупта), два знаменитых премьер-министра Магадской империи, принадлежали Кусумпуру или нынешнему Хагаулу в течение четвертого века до нашей эры. Чанакья дал начальное образование и обучение Чандагупте Маурье (Великому Императору Империи Магадх и основателю династии Маурьев) в этом самом месте. Под руководством Чанакьи могущественная Империя Магад распространилась от современной Индии, Бангладеш, Пакистана, Афганистана до Ирана после победы над силами Александра и Селевка. Тираническому правлению царя Дханананды над Магадом положил конец восстание Чанакьи после ареста, унижения и смертного приговора, вынесенного его отцу Чанаком тираническим королем Дхананандой. После этого Чандрагупта Маурья, ученик Чанакьи, стал королем-императором империи Магад, а Чанакья стал ее премьер-министром. Чанакья был великим ученым, экономистом, администратором, юристом, законодателем, а также очень проницательным националистом и проницательным политиком. Он был студентом университетов Такшашила или Таксила, а также работал ачарьей или профессором в том же университете. Под руководством Чанакьи могущественная Империя Магадх стала самой могущественной, самой влиятельной, самой развитой и богатейшей империей мира, а Паталипутра - самым красивым городом.
После 5-го века нашей эры Кусумпур был переименован в Хагаул в честь Хагола или Хагол Шастра, то есть астрономии, поскольку он был выдающимся центром Астрономической обсерватории (Хаголия Ведхашала), основанной Арьябхатой или Арьябхаттой для астрономических исследований и астрономических исследований. Арьябхатту называют отцом алгебры, геометрии и тригонометрии, концепции нуля (0) и десятичной системы.
Арьябхата, также называемый Арьябхатой I или Арьябхатой Старшим (родился в 476 году нашей эры, в Кусумапуре, недалеко от Паталипутры, или современной Патны в Индии), был астрономом и первым индийским математиком, чьи работы и история доступны современным ученым. Он также известен как Арьябхата I или Арьябхата Старший, чтобы отличить его от одноименного индийского математика 10-го века. Он процветал в Кусумапуре - недалеко от Паталипутры (Патна), тогдашней столицы династии Гуптов, - где он написал по крайней мере два произведения: Арьябхатия (c. 499) и теперь потерянный Арьябхатасиддханта.
Арьябхатасиддханта были распространены главным образом на северо-западе Индии и через династию Сасанидов (224–651 гг.) Ирана оказали глубокое влияние на развитие исламской астрономии. Его содержание до некоторой степени сохранилось в трудах Варахамихиры (процветание ок. 550 г.), Бхаскары I (расцвет ок. 629 г.), Брахмагупты (598 - ок. 665) и других. Это одна из первых астрономических работ, в которых начало каждого дня приходится на полночь.
Арьябхатия был особенно популярен в Южной Индии, где многочисленные математики в течение следующего тысячелетия писали комментарии. Работа написана в куплетах стихов и посвящена математике и астрономии. После введения, содержащего астрономические таблицы и систему обозначения фонематических чисел Арьябхаты, в которой числа представлены односложным согласным-гласным, работа разделена на три раздела: Ганита ("Математика"), Кала-крийя («Расчет времени») и Гола («Сфера»).
В Ганита Арьябхата называет первые 10 знаков после запятой и дает алгоритмы получения квадратных и кубических корней, используя десятичную систему счисления. Затем он обрабатывает геометрические измерения - используя 62 832/20 000 (= 3,1416) для π - и развивает свойства подобных прямоугольных треугольников и двух пересекающихся окружностей. Используя теорему Пифагора, он получил один из двух методов построения своей таблицы синусов. Он также понял, что разность синусов второго порядка пропорциональна синусу. Математические ряды, квадратные уравнения, сложные проценты (включающие квадратное уравнение), пропорции (соотношения) и решение различных линейных уравнений входят в число включенных арифметических и алгебраических тем. Общее решение Арьябхаты для линейных неопределенных уравнений, которое Бхаскара I назвал Куттакара («пульверизатор»), заключалась в разбиении проблемы на новые задачи с последовательно уменьшающимися коэффициентами - по сути, алгоритм Евклида и относился к методу непрерывных дробей.
С Кала-крийя Арьябхата обратился к астрономии - в частности, к изучению движения планет по эклиптике. Темы включают определения различных единиц времени, эксцентрические и эпициклические модели движения планет (видеть Гиппарх для более ранних греческих моделей), поправки планетарной долготы для различных земных местоположений и теория «владык часов и дней» (астрологическая концепция, используемая для определения благоприятного времени для действий).
Арьябхатия заканчивается сферической астрономией в Гола, где он применил плоскую тригонометрию к сферической геометрии, проецируя точки и линии на поверхности сферы на соответствующие плоскости. Темы включают предсказание солнечных и лунных затмений и явное утверждение, что видимое движение звезд на запад связано с вращением сферической Земли вокруг своей оси. Арьябхата также правильно приписал светимость Луны и планет отраженному солнечному свету.
Индийское правительство назвало свой первый спутник Aryabhata (запущенный в 1975 году) в его честь.
Рекомендации
- ^ а б «Перепись Индии 2001 г .: данные переписи 2001 г., включая города, села и поселки (предварительные)». Комиссия по переписи населения Индии. Архивировано из оригинал 16 июня 2004 г.. Получено 1 ноября 2008.
- ^ Falling Rain Genomics, Inc - Хагаул
- ^ https://www.census2011.co.in/data/town/801372-khagaul-bihar.html
