Магнитный диполь - Magnetic dipole
А магнитный диполь является пределом замкнутого цикла электрический ток или пара полюсов как размер[требуется разъяснение ] источника уменьшается до нуля при сохранении магнитный момент постоянный. Это магнитный аналог электрический диполь, но аналогия не идеальна. В частности, магнитный монополь, магнитный аналог электрический заряд, ни разу не наблюдался. Более того, одна из форм магнитного дипольного момента связана с фундаментальным квантовым свойством - вращение из элементарные частицы.
В магнитное поле Вокруг любого источника магнитного поля все больше похоже на поле магнитного диполя по мере увеличения расстояния от источника.
Внешнее магнитное поле, создаваемое магнитным дипольным моментом


В классическая физика, магнитное поле диполя рассчитывается как предел токовой петли или пары зарядов, когда источник сжимается до точки, сохраняя при этом магнитный момент м постоянный. Для токовой петли этот предел легче всего получить для векторный потенциал. Вне области источника этот потенциал равен (в Единицы СИ )[2]
с участием 4π r2 являясь поверхностью сферы радиуса р;
и плотность магнитного потока (напряженность B-поля) в теслас является[2]
Эквивалентно, если это единичный вектор в направлении [3]
В сферических координатах с магнитным моментом, направленным по оси z, если мы используем , то это соотношение можно выразить как
В качестве альтернативы можно получить скалярный потенциал сначала от предела магнитного полюса,
и, следовательно, напряженность магнитного поля (или напряженность H-поля) в ампер-витки на метр
Магнитное поле симметрично относительно вращений вокруг оси магнитного момента.
Внутреннее магнитное поле диполя
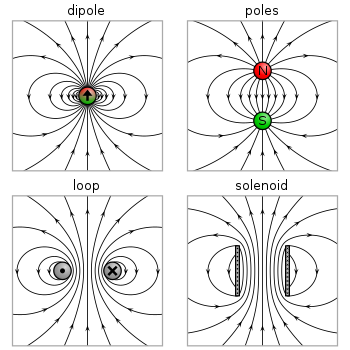
Две модели диполя (токовая петля и магнитные полюса) дают одинаковые предсказания для магнитного поля вдали от источника. Однако внутри области источника они дают разные прогнозы. Магнитное поле между полюсами имеет направление, противоположное магнитному моменту (который указывает от отрицательного заряда к положительному), в то время как внутри токовой петли оно находится в том же направлении (см. Рисунок справа). Понятно, что пределы этих полей также должны быть другими, поскольку источники уменьшаются до нулевого размера. Это различие имеет значение только в том случае, если дипольный предел используется для расчета полей внутри магнитного материала.
Если магнитный диполь формируется путем уменьшения и уменьшения токовой петли, но при сохранении постоянства произведения тока и площади, ограничивающее поле равно
где δ(р) это Дельта-функция Дирака в трех измерениях. В отличие от выражений в предыдущем разделе, этот предел верен для внутреннего поля диполя.
Если магнитный диполь сформирован путем взятия «северного полюса» и «южного полюса», приведения их все ближе и ближе друг к другу, но при сохранении постоянного произведения заряда магнитного полюса и расстояния, ограничивающее поле
Эти поля связаны B = μ0(ЧАС + M), где
это намагничивание.
Силы между двумя магнитными диполями
Сила F создаваемый одним дипольным моментом м1 на другом м2 разделены в пространстве вектором р можно рассчитать, используя:[4]
где р расстояние между диполями. Сила, действующая на м1 находится в противоположном направлении.
Крутящий момент можно получить по формуле
Диполярные поля из конечных источников
В магнитный скалярный потенциал ψ произведенный конечным источником, но внешним по отношению к нему, может быть представлен мультипольное расширение. Каждый член в разложении связан с характеристикой момент и потенциал, имеющий характерную скорость убывания с расстоянием р из источника. У монопольных моментов есть 1/р скорости убывания, дипольные моменты имеют 1/р2 скорости, квадрупольные моменты имеют 1/р3 скорость и так далее. Чем выше порядок, тем быстрее падает потенциал. Поскольку член низшего порядка, наблюдаемый в магнитных источниках, является дипольным членом, он доминирует на больших расстояниях. Поэтому на больших расстояниях любой магнитный источник выглядит как диполь того же магнитный момент.
Заметки
- ^ ЯВЛЯЕТСЯ. Грант, У. Р. Филлипс (2008). Электромагнетизм (2-е изд.). Manchester Physics, John Wiley & Sons. ISBN 978-0-471-92712-9.
- ^ а б Чау 2006, стр. 146–150
- ^ Джексон 1975, п. 182
- ^ Д.Дж. Гриффитс (2007). Введение в электродинамику (3-е изд.). Pearson Education. п. 276. ISBN 978-81-7758-293-2.
- ^ Фурлани 2001, п. 140
- ^ К.В. Юнг; П. Б. Ландекер; Д.Д. Виллани (1998). «Аналитическое решение для силы между двумя магнитными диполями» (PDF). Получено 24 ноября, 2012. Цитировать журнал требует
| журнал =(Помогите)
использованная литература
- Чоу, Тай Л. (2006). Введение в теорию электромагнетизма: современная перспектива. Джонс и Бартлетт Обучение. ISBN 978-0-7637-3827-3.CS1 maint: ref = harv (ссылка на сайт)
- Джексон, Джон Д. (1975). Классическая электродинамика (2-е изд.). Wiley. ISBN 0-471-43132-X.CS1 maint: ref = harv (ссылка на сайт)
- Фурлани, Эдвард П. (2001). Постоянный магнит и электромеханические устройства: материалы, анализ и применение. Академическая пресса. ISBN 0-12-269951-3.CS1 maint: ref = harv (ссылка на сайт)
- Шилль, Р. А. (2003). «Общее соотношение для векторного магнитного поля круговой токовой петли: более пристальный взгляд». IEEE Transactions on Magnetics. 39 (2): 961–967. Bibcode:2003ITM .... 39..961S. Дои:10.1109 / TMAG.2003.808597.


![{ displaystyle mathbf {B} ({ mathbf {r}}) = nabla times { mathbf {A}} = { frac { mu _ {0}} {4 pi}} left [ { frac {3 mathbf {r} ( mathbf {m} cdot mathbf {r})} {r ^ {5}}} - { frac { mathbf {m}} {r ^ {3} }}верно].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0991963d60a114ec41900b0eec04c944d03bb603)


![{ displaystyle mathbf {B} ({ mathbf {r}}) = { frac { mu _ {0}} {4 pi}} left [{ frac {3 mathbf { hat {r }} ( mathbf {m} cdot mathbf { hat {r}}) - mathbf {m}} {r ^ {3}}} right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac886c0ba5a8df671da92e098576f65bfeb304e0)



![{ displaystyle { mathbf {H}} ({ mathbf {r}}) = - nabla psi = { frac {1} {4 pi}} left [{ frac {3 mathbf { шляпа {r}} ( mathbf {m} cdot mathbf { hat {r}}) - mathbf {m}} {r ^ {3}}} right] = { frac { mathbf {B }} { mu _ {0}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/013db70805fbb46e718a5ac0fc04faa2f63dcd99)
![{ displaystyle mathbf {B} ( mathbf {r}) = { frac { mu _ {0}} {4 pi}} left [{ frac {3 mathbf { hat {r}} ( mathbf { hat {r}} cdot mathbf {m}) - mathbf {m}} {| mathbf {r} | ^ {3}}} + { frac {8 pi} {3 }} mathbf {m} delta ( mathbf {r}) right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe67ea7be3f7de2cc2f007ff3193b08520455b4d)
![{ displaystyle mathbf {H} ( mathbf {r}) = { frac {1} {4 pi}} left [{ frac {3 mathbf { hat {r}} ( mathbf { шляпа {r}} cdot mathbf {m}) - mathbf {m}} {| mathbf {r} | ^ {3}}} - { frac {4 pi} {3}} mathbf { m} delta ( mathbf {r}) right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1b635de5e52b7fd68571a72866d50392b0b7213)


![{ mathbf {F}} ({ mathbf {r}}, { mathbf {m}} _ {1}, { mathbf {m}} _ {2}) = { dfrac {3 mu _ { 0}} {4 pi r ^ {5}}} left [({ mathbf {m}} _ {1} cdot { mathbf {r}}) { mathbf {m}} _ {2} + ({ mathbf {m}} _ {2} cdot { mathbf {r}}) { mathbf {m}} _ {1} + ({ mathbf {m}} _ {1} cdot { mathbf {m}} _ {2}) { mathbf {r}} - { dfrac {5 ({ mathbf {m}} _ {1} cdot { mathbf {r}}) ({ mathbf {m}} _ {2} cdot { mathbf {r}})} {r ^ {2}}} { mathbf {r}} right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/d505434bbe3f60c36a43d3769e7d612c6fb1f27a)
