График Макги - McGee graph
| График Макги | |
|---|---|
 График Макги | |
| Названный в честь | У. Ф. МакГи |
| Вершины | 24 |
| Края | 36 |
| Радиус | 4 |
| Диаметр | 4[1] |
| Обхват | 7[1] |
| Автоморфизмы | 32[1] |
| Хроматическое число | 3[1] |
| Хроматический индекс | 3[1] |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Кубический Клетка Гамильтониан |
| Таблица графиков и параметров | |
в математический поле теория графов, то График Макги или (3-7) -клетка это 3-регулярный граф с 24 вершинами и 36 ребрами.[1]
Граф МакГи является единственным (3,7) -клетка (наименьший кубический граф обхвата 7). Это также самая маленькая кубическая клетка, которая не является Граф Мура.
Впервые обнаружен Саксом, но не опубликован,[2] график назван в честь Макги, опубликовавшего результат в 1960 году.[3] Затем граф МакГи был доказан как уникальная (3,7) -клетка Тутте в 1966 году.[4][5][6]
Граф МакГи требует как минимум восьми пересечений на любом его чертеже на плоскости. Это один из пяти неизоморфных графов, связанных как наименьший кубический граф, требующий восьми пересечений. Еще один из этих пяти графиков - это обобщенный граф Петерсена грамм(12,5), также известный как Науру график.[7][8]
График МакГи имеет радиус 4, диаметр 4, хроматическое число 3 и хроматический индекс 3. Это также 3-вершинно-связанный и 3-реберный график. Она имеет толщина книги 3 и номер очереди 2.[9]
Алгебраические свойства
В характеристический многочлен графа МакГи
- .
Группа автоморфизмов графа МакГи имеет порядок 32 и не действует транзитивно на свои вершины: есть две вершинные орбиты длиной 8 и 16. Граф МакГи - это наименьшая кубическая клетка, которая не является вершинно-транзитивный граф.[10][нужен лучший источник ]
Галерея
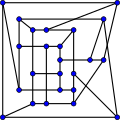
В номер перехода графа МакГи равно 8.

В хроматическое число графа МакГи равно 3.

В хроматический индекс графа МакГи равно 3.
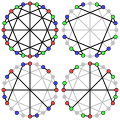
В ациклическое хроматическое число графа МакГи равно 3.

Альтернативный рисунок графа МакГи.
Рекомендации
- ^ а б c d е ж Вайсштейн, Эрик В. "График МакГи". MathWorld.
- ^ Kárteszi, F. «Piani finit ciclici come risoluzioni di un certo проблема di minimo». Болл. ООН. Мат. Ital. 15, 522-528, 1960
- ^ Макги, В. Ф. "Минимальный кубический граф седьмого обхвата". Канад. Математика. Бык. 3, 149-152, 1960 г.
- ^ Тутте, В. Т. Связность в графах. Торонто, Онтарио: Университет Торонто Press, 1966 г.
- ^ Вонг, П. К. «Клетки - обзор». J. Graph Th. 6, 1-22, 1982 г.
- ^ Brouwer, A.E .; Коэн, А. М .; и Ноймайер А. Дистанционные регулярные графы. Нью-Йорк: Springer-Verlag, стр. 209, 1989 г.
- ^ Слоан, Н. Дж. А. (ред.). «Последовательность A110507 (Количество узлов в наименьшем кубическом графе с числом пересечения n)». В Он-лайн энциклопедия целочисленных последовательностей. Фонд OEIS.
- ^ Пегг, Э. Т.; Эксу, Г. (2009), «Графики пересечения чисел», Математика журнал, 11.
- ^ Джессика Вольц, Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.
- ^ Бонди, Дж. А., Мурти, США. Теория графов с приложениями. Нью-Йорк: Северная Голландия, стр. 237, 1976.






