Многомерная дискретная свертка - Википедия - Multidimensional discrete convolution

При обработке сигналов многомерная дискретная свертка относится к математической операции между двумя функциями ж и грамм на п-мерная решетка, которая порождает третью функцию, также п-размеры. Многомерная дискретная свертка является дискретным аналогом многомерная свертка функций на евклидовом пространстве. Это также частный случай свертка по группам когда группа это группа п-наборы целых чисел.

Определение

Постановка проблемы и основные сведения

Как и в одномерном случае, звездочка используется для обозначения операции свертки. Количество измерений в данной операции отображается в количестве звездочек. Например, M-мерная свертка будет записана с M звездочки. Следующее представляет собой M-мерная свертка дискретных сигналов:

${ displaystyle y (n_ {1}, n_ {2}, ..., n_ {M}) = x (n_ {1}, n_ {2}, ..., n_ {M}) * { overset {M} { cdots}} * h (n_ {1}, n_ {2}, ..., n_ {M})}$

Для сигналов с дискретными значениями эта свертка может быть напрямую вычислена с помощью следующего:

${ displaystyle sum _ {k_ {1} = - infty} ^ { infty} sum _ {k_ {2} = - infty} ^ { infty} ... sum _ {k_ {M} = - infty} ^ { infty} h (k_ ​​{1}, k_ {2}, ..., k_ {M}) x (n_ {1} -k_ {1}, n_ {2} -k_ { 2}, ..., n_ {M} -k_ {M})}$

Результирующая выходная область поддержки дискретной многомерной свертки будет определяться на основе размера и областей поддержки двух входных сигналов.

Перечислены несколько свойств оператора двумерной свертки. Обратите внимание, что они также могут быть расширены для сигналов ${ displaystyle N}$-размеры.

Коммутативная собственность:

${ Displaystyle х ** ч = ч ** х}$

Сопутствующее имущество:

${ Displaystyle (х ** ч) ** г = х ** (ч ** г)}$

Распределительное свойство:

${ Displaystyle х ** (ч + г) = (х ** ч) + (х ** г)}$

Эти свойства показаны на рисунке ниже. Учитывая некоторый вклад ${ Displaystyle х (п_ {1}, п_ {2})}$ который входит в фильтр с импульсной характеристикой ${ displaystyle h (n_ {1}, n_ {2})}$ а потом еще один фильтр с импульсной характеристикой ${ displaystyle g (n_ {1}, n_ {2})}$, выход определяется как ${ Displaystyle у (п_ {1}, п_ {2})}$. Предположим, что выход первого фильтра определяется выражением ${ Displaystyle ш (п_ {1}, п_ {2})}$, это означает, что:

${ displaystyle w = x ** h}$

Кроме того, эта промежуточная функция затем сворачивается с импульсной характеристикой второго фильтра, и, таким образом, выходной сигнал может быть представлен следующим образом:

${ displaystyle y = w ** g = (x ** h) ** g}$

Используя свойство ассоциативности, это можно переписать следующим образом:

${ Displaystyle у = х ** (ч ** г)}$

Это означает, что эквивалентный импульсный отклик для каскадной системы определяется следующим образом:

${ displaystyle h_ {eq} = h ** g}$

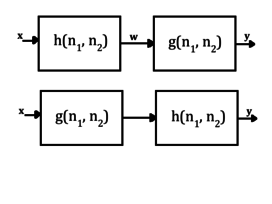
Аналогичный анализ можно провести на наборе параллельных систем, показанных ниже.

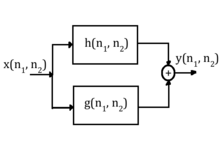
В этом случае ясно, что:

${ Displaystyle у = (х ** ч) + (х ** г)}$

Используя закон распределения, показано, что:

${ Displaystyle у = х ** (ч + г)}$

Это означает, что в случае параллельной системы эквивалентный импульсный отклик обеспечивается:

${ displaystyle h_ {eq} = h + g}$

Эквивалентные импульсные характеристики как в каскадных, так и в параллельных системах можно обобщить на системы с ${ displaystyle N}$-количество фильтров.^[1]

Мотивация и приложения

Свертка в одном измерении была мощным открытием, которое позволило вводить и выводить линейную инвариантную относительно сдвига (LSI) систему (см. Теория систем LTI ), чтобы их можно было легко сравнить, если была известна импульсная характеристика системы фильтров. Это понятие переносится и на многомерную свертку, поскольку простое знание импульсной характеристики многомерного фильтра также позволяет проводить прямое сравнение между входом и выходом системы. Это очень важно, поскольку некоторые из сигналов, которые передаются в современном цифровом мире, имеют множество измерений, включая изображения и видео. Подобно одномерной свертке, многомерная свертка позволяет вычислять выходные данные системы LSI для заданного входного сигнала.

Например, рассмотрим изображение, которое передается по беспроводной сети, подверженной оптико-электронным помехам. Возможные источники шума включают ошибки в канальной передаче, аналого-цифровой преобразователь и датчик изображения. Обычно шум, вызванный каналом или датчиком, создает пространственно-независимые высокочастотные компоненты сигнала, которые превращаются в произвольные светлые и темные пятна на фактическом изображении. Чтобы избавить данные изображения от высокочастотного спектрального содержания, его можно умножить на частотную характеристику фильтра нижних частот, который, основываясь на теореме свертки, эквивалентен свертке сигнала во временной / пространственной области на импульсная характеристика фильтра нижних частот. Некоторые импульсные характеристики, которые это делают, показаны ниже.^[2]

В дополнение к фильтрации спектрального содержимого многомерная свертка может реализовывать обнаружение границ и сглаживание. Это опять же полностью зависит от значений импульсной характеристики, которая используется для свертки с входным изображением. Типичные импульсные характеристики для обнаружения края показаны ниже.

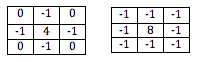
В дополнение к обработке изображений, многомерная свертка может быть реализована для поддержки множества других приложений. Поскольку фильтры широко распространены в системах цифровой связи, любой системе, которая должна передавать многомерные данные, помогают методы фильтрации. Они используются при обработке видео в реальном времени, анализе нейронных сетей, анализе цифровых геофизических данных и многом другом.^[3]

Одним из типичных искажений, которые возникают во время приложений захвата или передачи изображений и видео, является размытие, вызванное процессом фильтрации нижних частот. Введенное размытие можно смоделировать с помощью гауссовой фильтрации нижних частот.

Декомпозиция строки-столбца с разделяемыми сигналами

Разделимые сигналы

Сигнал называется отделяемый если его можно записать как произведение нескольких одномерных сигналов.^[1] Математически это выражается следующим образом:

${ displaystyle x (n_ {1}, n_ {2}, ..., n_ {M}) = x (n_ {1}) x (n_ {2}) ... x (n_ {M})}$

Некоторые легко распознаваемые разделяемые сигналы включают функцию единичного шага и импульсную функцию дельта-дирака.

${ displaystyle u (n_ {1}, n_ {2}, ..., n_ {M}) = u (n_ {1}) u (n_ {2}) ... u (n_ {M})}$ (функция единичного шага)

${ displaystyle delta (n_ {1}, n_ {2}, ..., n_ {M}) = delta (n_ {1}) delta (n_ {2}) ... delta (n_ { M})}$ (импульсная функция дельта-дирака)

Свертка - это линейная операция. Из этого следует, что многомерная свертка разделяемых сигналов может быть выражена как произведение многих одномерных сверток. Например, рассмотрим случай, когда Икс и час обе разделимые функции.

${ displaystyle x (n_ {1}, n_ {2}) ** h (n_ {1}, n_ {2}) = sum _ {k_ {1} = - infty} ^ { infty} sum _ {k_ {2} = - infty} ^ { infty} h (k_ ​​{1}, k_ {2}) x (n_ {1} -k_ {1}, n_ {2} -k_ {2}) }$

Применяя свойства отделимости, это можно переписать следующим образом:

${ displaystyle x (n_ {1}, n_ {2}) ** h (n_ {1}, n_ {2}) = { bigg (} sum _ {k_ {1} = - infty} ^ { infty} h (k_ ​​{1}) x (n_ {1} -k_ {1}) { bigg)} { bigg (} sum _ {k_ {2} = - infty} ^ { infty} h (k_ ​​{2}) x (n_ {2} -k_ {2}) { bigg)}}$

Легко видеть, что это сводится к произведению одномерных сверток:

${ Displaystyle х (п_ {1}, п_ {2}) ** ч (п_ {1}, п_ {2}) = { bigg [} х (п_ {1}) * ч (п_ {1}) { bigg]} { bigg [} x (n_ {2}) * h (n_ {2}) { bigg]}}$

Затем этот вывод можно распространить на свертку двух разделимых M-размерные сигналы следующим образом:

${ displaystyle x (n_ {1}, n_ {2}, ..., n_ {M}) * { overset {M} { cdots}} * h (n_ {1}, n_ {2} ,. .., n_ {M}) = { bigg [} x (n_ {1}) * h (n_ {1}) { bigg]} { bigg [} x (n_ {2}) * h (n_ {2}) { bigg]} ... { bigg [} x (n_ {M}) * h (n_ {M}) { bigg]}}$

Итак, когда два сигнала разделимы, многомерная свертка может быть вычислена путем вычисления ${ displaystyle n_ {M}}$ одномерные свертки.

Декомпозиция строки-столбца

Метод строка-столбец может применяться, когда один из сигналов в свертке разделяется. Этот метод использует свойства разделимости для достижения метода вычисления свертки двух многомерных сигналов, который является более эффективным в вычислительном отношении, чем прямое вычисление каждой выборки (при условии, что один из сигналов является разделимым).^[4] Ниже показано математическое обоснование подхода декомпозиции строки-столбца (обычно ${ displaystyle h (n_ {1}, n_ {2})}$ - разделимый сигнал):

${ displaystyle { begin {align} y (n_ {1}, n_ {2}) & = sum _ {k_ {1} = - infty} ^ { infty} sum _ {k_ {2} = - infty} ^ { infty} h (k_ ​​{1}, k_ {2}) x (n_ {1} -k_ {1}, n_ {2} -k_ {2}) & = sum _ {k_ {1} = - infty} ^ { infty} sum _ {k_ {2} = - infty} ^ { infty} h_ {1} (k_ {1}) h_ {2} (k_ { 2}) x (n_ {1} -k_ {1}, n_ {2} -k_ {2}) & = sum _ {k_ {1} = - infty} ^ { infty} h_ {1 } (k_ {1}) { Bigg [} sum _ {k_ {2} = - infty} ^ { infty} h_ {2} (k_ {2}) x (n_ {1} -k_ {1 }, n_ {2} -k_ {2}) { Bigg]} end {align}}}$

Значение ${ displaystyle sum _ {k_ {2} = - infty} ^ { infty} h_ {2} (k_ {2}) x (n_ {1} -k_ {1}, n_ {2} -k_ { 2})}$ теперь можно повторно использовать при оценке других ${ displaystyle y}$ ценности с общим значением ${ displaystyle n_ {2}}$:

${ displaystyle { begin {align} y (n_ {1} + delta, n_ {2}) & = sum _ {k_ {1} = - infty} ^ { infty} h_ {1} (k_ {1}) { Bigg [} sum _ {k_ {2} = - infty} ^ { infty} h_ {2} (k_ {2}) x (n_ {1} - [k_ {1} - delta], n_ {2} -k_ {2}) { Bigg]} & = sum _ {k_ {1} = - infty} ^ { infty} h_ {1} (k_ {1} + delta) { Bigg [} sum _ {k_ {2} = - infty} ^ { infty} h_ {2} (k_ {2}) x (n_ {1} -k_ {1}, n_ {2} -k_ {2}) { Bigg]} конец {выровнено}}}$

Таким образом, результирующую свертку можно эффективно вычислить, сначала выполнив операцию свертки для всех строк ${ Displaystyle х (п_ {1}, п_ {2})}$, а затем во всех его столбцах. Этот подход может быть дополнительно оптимизирован, если учесть, как осуществляется доступ к памяти в процессоре компьютера.

Процессор загрузит данные сигнала, необходимые для данной операции. Для современных процессоров данные будут загружаться из памяти в кэш процессора, который имеет более быстрое время доступа, чем память. Сам кеш разбит на строки. Когда строка кэша загружается из памяти, одновременно загружается несколько операндов данных. Рассмотрим оптимизированный случай, когда строка данных сигнала может полностью уместиться в кэш-памяти процессора. Этот конкретный процессор сможет эффективно получать доступ к данным по строкам, но не по столбцам, поскольку разные операнды данных в одном столбце будут лежать в разных строках кэша.^[5] Чтобы воспользоваться преимуществами способа доступа к памяти, более эффективно транспонировать набор данных, а затем ось его по строкам, а не пытаться обращаться к нему по столбцам. Затем алгоритм становится:

1. Разделить разделяемый двумерный сигнал ${ displaystyle h (n_ {1}, n_ {2})}$ в два одномерных сигнала ${ displaystyle h_ {1} (n_ {1})}$ и ${ displaystyle h_ {2} (n_ {2})}$
2. Выполните построчную свертку горизонтальных компонентов сигнала. ${ Displaystyle х (п_ {1}, п_ {2})}$ с помощью ${ displaystyle h_ {1} (n_ {1})}$ чтобы получить ${ displaystyle g (n_ {1}, n_ {2})}$
3. Транспонируйте вертикальные компоненты сигнала ${ displaystyle g (n_ {1}, n_ {2})}$ в результате шага 2.
4. Выполните построчную свертку транспонированных вертикальных компонентов ${ displaystyle g (n_ {1}, n_ {2})}$ чтобы получить желаемый результат ${ Displaystyle у (п_ {1}, п_ {2})}$

Ускорение вычислений за счет декомпозиции строки-столбца

Рассмотрим случай, когда изображение размера ${ Displaystyle X раз Y}$ проходит через отделяемый фильтр размером ${ displaystyle J times K}$. Само изображение не отделимо. Если результат вычисляется с использованием подхода прямой свертки без использования разделимости фильтра, это потребует приблизительно ${ displaystyle XYJK}$ умножения и сложения. Если учесть разделимость фильтра, фильтрацию можно проводить в два этапа. Первый шаг будет иметь ${ displaystyle XYJ}$ умножения и сложения, а второй шаг будет иметь ${ displaystyle XYK}$, в результате чего всего ${ displaystyle XYJ + XYK}$ или же ${ Displaystyle XY (J + K)}$ умножения и сложения.^[6] Сравнение вычислительной сложности прямой и разделяемой свертки дается на следующем изображении:

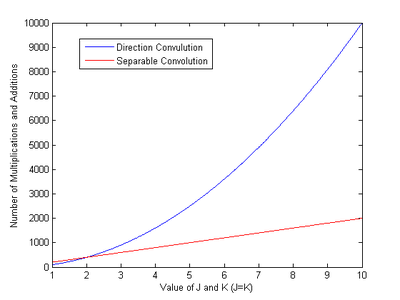
Круговая свертка многомерных дискретных сигналов.

Предпосылка, лежащая в основе подхода круговой свертки к многомерным сигналам, состоит в том, чтобы установить связь между Теорема свертки и Дискретное преобразование Фурье (ДПФ), который можно использовать для вычисления свертки между двумя дискретными сигналами конечной протяженности.^[7]

Теорема о свертке в многомерности

Для одномерных сигналов Теорема свертки заявляет, что преобразование Фурье свертки между двумя сигналами равно произведению преобразований Фурье этих двух сигналов. Таким образом, свертка во временной области равна умножению в частотной области. Математически этот принцип выражается следующим образом:

Этот принцип можно напрямую распространить на сигналы многих измерений.Это свойство легко распространяется на использование с Дискретное преобразование Фурье (ДПФ) следующим образом (обратите внимание, что линейная свертка заменяется круговой сверткой, где ${ displaystyle otimes}$ используется для обозначения операции круговой свертки размера ${ displaystyle N}$):

${ Displaystyle Y (N) = H (N) otimes x (n) longleftrightarrow Y (k) = H (k) X (k)}$

При работе с многомерными сигналами:

Круговые извилины здесь будут размером ${ displaystyle N_ {1}, N_ {2}, ..., N_ {M}}$.

Подход круговой свертки

Мотивация использования подхода круговой свертки заключается в том, что он основан на ДПФ. Предпосылка круговой свертки состоит в том, чтобы взять ДПФ входных сигналов, умножить их вместе, а затем взять обратное ДПФ. Необходимо соблюдать осторожность, чтобы использовать достаточно большое ДПФ, чтобы не возникало наложения спектров. ДПФ вычислимо численно при работе с сигналами конечной протяженности. Одним из преимуществ этого подхода является то, что, поскольку он требует использования ДПФ и обратного ДПФ, можно использовать эффективные алгоритмы, такие как Быстрое преобразование Фурье (БПФ). Круговая свертка также может быть вычислена во временной / пространственной области, а не только в частотной области.

Выбор размера ДПФ, чтобы избежать сглаживания

Рассмотрим следующий случай, когда два сигнала конечной протяженности Икс и час принимаются. Для обоих сигналов существует соответствующее ДПФ:

${ displaystyle x (n_ {1}, n_ {2}) longleftrightarrow X (k_ {1}, k_ {2})}$ и ${ displaystyle h (n_ {1}, n_ {2}) longleftrightarrow H (k_ {1}, k_ {2})}$

Регион поддержки ${ Displaystyle х (п_ {1}, п_ {2})}$ является ${ Displaystyle 0 Leq N_ {1} Leq P_ {1} -1}$ и ${ Displaystyle 0 Leq N_ {2} Leq P_ {2} -1}$ и регион поддержки ${ displaystyle h (n_ {1}, n_ {2})}$ является ${ Displaystyle 0 Leq N_ {1} Leq Q_ {1} -1}$ и ${ Displaystyle 0 Leq N_ {2} Leq Q_ {2} -1}$.

Линейная свертка этих двух сигналов будет дана как:

Учитывая регионы поддержки ${ Displaystyle х (п_ {1}, п_ {2})}$ и ${ displaystyle h (n_ {1}, n_ {2})}$, регион поддержки ${ displaystyle y_ {linear} (n_ {1}, n_ {2})}$ тогда будет дано следующее:

Основываясь на регионах поддержки двух сигналов, ДПФ размера ${ displaystyle N_ {1} times N_ {2}}$ должен использоваться там, где ${ Displaystyle N_ {1} geq max (P_ {1}, Q_ {1})}$ и ${ Displaystyle N_ {2} geq max (P_ {2}, Q_ {2})}$ поскольку для обоих сигналов необходимо использовать ДПФ одинакового размера. В случае, когда требуется размер ДПФ, превышающий размер сигнала, сигнал дополняется нулями, пока не достигнет требуемой длины. После умножения ДПФ и взятия обратного ДПФ на результат результирующая круговая свертка определяется следующим образом:

${ displaystyle y_ {круговой} (n_ {1}, n_ {2}) = sum _ {r_ {1}} sum _ {r_ {2}} { Bigg [} sum _ {m_ {1} = 0} ^ {Q_ {1} -1} sum _ {m_ {2} = 0} ^ {Q_ {2} -1} h (m_ {1}, m_ {2}) x (n_ {1} -m_ {1} -r_ {1} N_ {1}, n_ {2} -m_ {2} -r_ {2} N_ {2}) { Bigg]}}$ за ${ displaystyle (n_ {1}, n_ {2}) in R_ {N_ {1} N_ {2}}}$

${ Displaystyle R_ {N_ {1} N_ {2}} треугольник {(n_ {1}, n_ {2}): 0 leq n_ {1} leq N_ {1} -1,0 leq n_ {2} leq N_ {2} -1 }}$

Результатом будет то, что ${ displaystyle y_ {круговой} (n_ {1}, n_ {2})}$ будет версией результата линейной свертки с пространственным алиасом ${ displaystyle y_ {linear} (n_ {1}, n_ {2})}$. Это можно выразить следующим образом:

${ displaystyle y_ {круговой} (n_ {1}, n_ {2}) = sum _ {r_ {1}} sum _ {r_ {2}} y_ {linear} (n_ {1} -r_ {1 } N_ {1}, n_ {2} -r_ {2} N_ {2}) { mathrm {, , , для , , ,}} (n_ {1}, n_ {2}) in R_ {N_ {1} N_ {2}}}$

Затем, чтобы избежать наложения спектров между репликами с пространственным псевдонимом, ${ displaystyle N_ {1}}$ и ${ displaystyle N_ {2}}$ должен быть выбран так, чтобы удовлетворять следующим условиям:

${ Displaystyle N_ {1} geq P_ {1} + Q_ {1} -1}$

${ Displaystyle N_ {2} geq P_ {2} + Q_ {2} -1}$

Если эти условия выполнены, то результаты круговой свертки будут равны результатам линейной свертки (принимая основной период круговой свертки в качестве области опоры). То есть:

${ displaystyle y_ {круговой} (n_ {1}, n_ {2}) = y_ {linear} (n_ {1}, n_ {2})}$ за ${ displaystyle (n_ {1}, n_ {2}) in R_ {N_ {1} N_ {2}}}$

Краткое описание процедуры с использованием ДПФ

Таким образом, теорему о свертке и круговую свертку можно использовать следующим образом для достижения результата, равного выполнению линейной свертки:^[8]

1. выбирать ${ displaystyle N_ {1}}$ и ${ displaystyle N_ {2}}$ удовлетворить ${ Displaystyle N_ {1} geq P_ {1} + Q_ {1} -1}$ и ${ Displaystyle N_ {2} geq P_ {2} + Q_ {2} -1}$
2. Обнулить сигналы ${ displaystyle h (n_ {1}, n_ {2})}$ и ${ Displaystyle х (п_ {1}, п_ {2})}$ так что они оба ${ displaystyle N_ {1} times N_ {2}}$ по размеру
3. Вычислить ДПФ обоих ${ displaystyle h (n_ {1}, n_ {2})}$ и ${ Displaystyle х (п_ {1}, п_ {2})}$
4. Умножьте результаты ДПФ, чтобы получить ${ Displaystyle Y (k_ {1}, k_ {2}) = H (k_ {1}, k_ {2}) X (k_ {1}, k_ {2})}$
5. Результат IDFT ${ displaystyle Y (k_ {1}, k_ {2})}$ тогда будет равно результату выполнения линейной свертки двух сигналов

Перекрытие и добавление

Другой метод выполнения многомерной свертки - это перекрыть и добавить подход.Этот метод помогает снизить вычислительную сложность, часто связанную с многомерными свертками из-за огромных объемов данных, присущих современным цифровым системам.^[9] Для краткости в качестве примера используется двумерный случай, но те же концепции можно распространить на несколько измерений.

Рассмотрим двумерную свертку с помощью прямого вычисления:

${ displaystyle y (n_ {1}, n_ {2}) = sum _ {k_ {1} = - infty} ^ { infty} sum _ {k_ {2} = - infty} ^ { infty} x (n_ {1} -k_ {1}, n_ {2} -k_ {2}) h (k_ ​​{1}, k_ {2})}$

Предполагая, что выходной сигнал ${ Displaystyle у (п_ {1}, п_ {2})}$ имеет N ненулевых коэффициентов, а импульсный отклик имеет M ненулевых отсчетов, это прямое вычисление потребует MN умножений и MN - 1 сложения для вычисления. Вместо этого при использовании БПФ частотная характеристика фильтра и преобразование Фурье входа должны быть сохранены в памяти.^[10] Огромные объемы вычислений и чрезмерное использование памяти для хранения создают проблемную проблему по мере добавления дополнительных измерений. Именно здесь на помощь приходит метод перекрытия и добавления свертки.

Разложение на более мелкие блоки свертки

Вместо того, чтобы выполнять свертку блоков информации в целом, информация может быть разбита на более мелкие блоки измерений. ${ displaystyle L_ {1}}$Икс${ displaystyle L_ {2}}$ что приводит к меньшему количеству БПФ, меньшей вычислительной сложности и меньшему объему памяти. Математически это можно выразить следующим образом:

${ displaystyle x (n_ {1}, n_ {2}) = sum _ {i = 1} ^ {P_ {1}} sum _ {j = 1} ^ {P_ {2}} x_ {ij} (n_ {1}, n_ {2})}$

куда ${ Displaystyle х (п_ {1}, п_ {2})}$ представляет ${ displaystyle N_ {1}}$Икс${ displaystyle N_ {2}}$ входной сигнал, который представляет собой сумму ${ Displaystyle P_ {1} P_ {2}}$ блочные сегменты, с ${ Displaystyle P_ {1} = N_ {1} / L_ {1}}$ и ${ Displaystyle P_ {2} = N_ {2} / L_ {2}}$.

Для получения выходного сигнала выполняется двумерная свертка:

${ displaystyle y (n_ {1}, n_ {2}) = x (n_ {1}, n_ {2}) ** h (n_ {1}, n_ {2})}$

Замена на ${ Displaystyle х (п_ {1}, п_ {2})}$ приводит к следующему:

${ displaystyle y (n_ {1}, n_ {2}) = sum _ {i = 1} ^ {P_ {1}} sum _ {j = 1} ^ {P_ {2}} x_ {ij} (n_ {1}, n_ {2}) ** h (n_ {1}, n_ {2})}$

Эта свертка добавляет больше сложности, чем прямая свертка; однако, поскольку он интегрирован с быстрой сверткой БПФ, сложение с перекрытием выполняется быстрее и является более эффективным с точки зрения памяти методом, что делает его практичным для больших наборов многомерных данных.

Нарушение процедуры

Позволять ${ displaystyle h (n_ {1}, n_ {2})}$ иметь размер ${ displaystyle M_ {1} times M_ {2}}$:

1. Разрыв ввода ${ Displaystyle х (п_ {1}, п_ {2})}$ в неперекрывающиеся блоки размеров ${ displaystyle L_ {1} times L_ {2}}$.
2. Нулевая площадка ${ displaystyle h (n_ {1}, n_ {2})}$ такой, что он имеет размеры (${ displaystyle L_ {1} + M_ {1} -1}$) ${ displaystyle times}$ (${ displaystyle L_ {2} + M_ {2} -1}$).
3. Используйте DFT, чтобы получить ${ Displaystyle Н (к_ {1}, к_ {2})}$.
4. Для каждого входного блока:
   1. Нулевая площадка ${ displaystyle x_ {ij} (n_ {1}, n_ {2})}$ иметь размеры (${ displaystyle L_ {1} + M_ {1} -1}$) ${ displaystyle times}$ (${ displaystyle L_ {2} + M_ {2} -1}$).
   2. Возьмите дискретное преобразование Фурье каждого блока, чтобы получить ${ Displaystyle X_ {ij} (k_ {1}, k_ {2})}$.
   3. Умножьте, чтобы получить ${ Displaystyle Y_ {ij} (k_ {1}, k_ {2}) = X_ {ij} (k_ {1}, k_ {2}) H (k_ {1}, k_ {2})}$.
   4. Возьмем обратное дискретное преобразование Фурье ${ displaystyle Y_ {ij} (k_ {1}, k_ {2})}$ получить ${ displaystyle y_ {ij} (n_ {1}, n_ {2})}$.
5. Находить ${ Displaystyle у (п_ {1}, п_ {2})}$ путем перекрытия и добавления последнего ${ displaystyle (M_ {1} -1)}$${ displaystyle times}$ ${ displaystyle (M_ {2} -1)}$ образцы ${ displaystyle y_ {ij} (n_ {1}, n_ {2})}$ с первым ${ displaystyle (M_ {1} -1)}$ ${ displaystyle times}$${ displaystyle (M_ {2} -1)}$ образцы ${ displaystyle y_ {я + 1, j + 1} (n_ {1}, n_ {2})}$ чтобы получить результат.^[11]

Графический метод работы

Чтобы нагляднее представить метод сложения с перекрытием, на следующих иллюстрациях этот метод рассматривается графически. Предположим, что вход ${ Displaystyle х (п_ {1}, п_ {2})}$ имеет квадратную опору длиной N как в вертикальном, так и в горизонтальном направлениях, как показано на рисунке ниже. Затем он разбивается на четыре меньших сегмента таким образом, что теперь он состоит из четырех меньших квадратов. Каждый блок совокупного сигнала имеет размеры ${ Displaystyle (N / 2)}$ ${ displaystyle times}$ ${ Displaystyle (N / 2)}$.

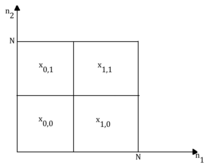
Затем каждый компонент свертывается с импульсной характеристикой фильтра. Обратите внимание, что здесь можно визуализировать преимущество такой реализации, поскольку каждая из этих сверток может быть распараллелена на компьютере, если компьютер имеет достаточно памяти и ресурсов для одновременного хранения и вычислений.

На рисунке ниже первый график слева представляет свертку, соответствующую компоненту входных данных. ${ displaystyle x_ {0,0}}$ с соответствующей импульсной характеристикой ${ displaystyle h (n_ {1}, n_ {2})}$. Справа от него вход ${ displaystyle x_ {1,0}}$ затем сворачивается с импульсной характеристикой ${ displaystyle h (n_ {1}, n_ {2})}$.

Тот же процесс выполняется для двух других входных данных соответственно, и они накапливаются вместе, чтобы сформировать свертку. Это изображено слева.

Предположим, что импульсная характеристика фильтра ${ displaystyle h (n_ {1}, n_ {2})}$ имеет регион поддержки ${ Displaystyle (N / 8)}$ в обоих измерениях. Это означает, что каждая свертка сворачивает сигналы с размерами ${ Displaystyle (N / 2)}$ ${ displaystyle times}$ ${ Displaystyle (N / 8)}$ в обоих ${ displaystyle n_ {1}}$ и ${ displaystyle n_ {2}}$ направлений, что приводит к перекрытию (выделено синим), поскольку длина каждой отдельной свертки эквивалентна:

${ Displaystyle (N / 2)}$ ${ displaystyle +}$${ Displaystyle (N / 8)}$ ${ displaystyle -}$${ displaystyle 1}$ = ${ displaystyle (5/8) N-1}$

в обоих направлениях. Светло-синяя часть коррелирует с перекрытием между двумя соседними свертками, тогда как более темная синяя часть коррелирует с перекрытием между всеми четырьмя свертками. Все эти перекрывающиеся части складываются вместе в дополнение к сверткам, чтобы сформировать комбинированную свертку. ${ Displaystyle у (п_ {1}, п_ {2})}$.^[12]

Перекрытие и сохранение

Метод перекрытия и сохранения, как и метод перекрытия и добавления, также используется для уменьшения вычислительной сложности, связанной с дискретными свертками. Этот метод в сочетании с БПФ позволяет фильтровать огромные объемы данных через цифровую систему, при этом минимизируя необходимое пространство памяти, используемое для вычислений над массивными массивами данных.

Сравнение с перекрытием и сложением

Метод перекрытия и сохранения очень похож на методы перекрытия и добавления с некоторыми заметными исключениями. Метод сложения с перекрытием включает в себя линейную свертку сигналов с дискретным временем, тогда как метод с сохранением перекрытия использует принцип круговой свертки. Кроме того, метод перекрытия и сохранения использует только одноразовое заполнение нулями импульсной характеристики, тогда как метод добавления перекрытия включает заполнение нулями для каждой свертки на каждом входном компоненте. Вместо использования нулевого заполнения для предотвращения сглаживания во временной области, как его аналог с перекрытием-добавлением, overlap-save просто отбрасывает все точки сглаживания и сохраняет предыдущие данные в одном блоке для копирования в свертку для следующего блока.

В одном измерении различия в показателях производительности и хранилища между двумя методами минимальны. Однако в случае многомерной свертки метод сохранения с перекрытием предпочтительнее метода сложения с перекрытием с точки зрения скорости и возможностей хранения.^[13] Как и в случае наложения и добавления, процедура вызывает двумерный случай, но может быть легко расширена на все многомерные процедуры.

Нарушение процедуры

Позволять ${ displaystyle h (n_ {1}, n_ {2})}$ иметь размер ${ displaystyle M_ {1} times M_ {2}}$:

1. Вставлять ${ displaystyle (M_ {1} -1)}$ колонны и ${ displaystyle (M_ {2} -1)}$ строки нулей в начале входного сигнала ${ Displaystyle х (п_ {1}, п_ {2})}$ в обоих измерениях.
2. Разделите соответствующий сигнал на перекрывающиеся сегменты размеров (${ displaystyle L_ {1} + M_ {1} -1}$)${ displaystyle times}$(${ displaystyle L_ {2} + M_ {2} -1}$), в котором каждый двумерный блок будет перекрываться на ${ displaystyle (M_ {1} -1)}$ ${ displaystyle times}$ ${ displaystyle (M_ {2} -1)}$.
3. Нулевая площадка ${ displaystyle h (n_ {1}, n_ {2})}$ такой, что он имеет размеры (${ displaystyle L_ {1} + M_ {1} -1}$)${ displaystyle times}$(${ displaystyle L_ {2} + M_ {2} -1}$).
4. Используйте DFT, чтобы получить ${ Displaystyle Н (к_ {1}, к_ {2})}$.
5. Для каждого входного блока:
   1. Возьмите дискретное преобразование Фурье каждого блока, чтобы получить ${ Displaystyle X_ {ij} (k_ {1}, k_ {2})}$.
   2. Умножьте, чтобы получить ${ Displaystyle Y_ {ij} (k_ {1}, k_ {2}) = X_ {ij} (k_ {1}, k_ {2}) H (k_ {1}, k_ {2})}$.
   3. Возьмем обратное дискретное преобразование Фурье ${ displaystyle Y_ {ij} (k_ {1}, k_ {2})}$ получить ${ displaystyle y_ {ij} (n_ {1}, n_ {2})}$.
   4. Избавьтесь от первого ${ displaystyle (M_ {1} -1)}$${ displaystyle times}$${ displaystyle (M_ {2} -1)}$ для каждого выходного блока ${ displaystyle y_ {ij} (n_ {1}, n_ {2})}$.
6. Находить ${ Displaystyle у (п_ {1}, п_ {2})}$ прикрепив последний ${ Displaystyle (L_ {1} раз L_ {2})}$ образцы для каждого выходного блока ${ displaystyle y_ {ij} (n_ {1}, n_ {2})}$.^[11]

Преобразование спирали

Подобно разложению строки-столбца, преобразование спирали вычисляет многомерную свертку путем включения одномерных сверточных свойств и операторов. Однако вместо использования разделимости сигналов он отображает декартово координатное пространство в спиральное координатное пространство, позволяя отображать многомерное пространство в одномерное пространство.

Многомерная свертка с методами одномерной свертки

Чтобы понять преобразование спирали, полезно сначала понять, как многомерная свертка может быть разбита на одномерную свертку. Предположим, что два сигнала для свертки ${ displaystyle X_ {M times N}}$ и ${ displaystyle Y_ {K times L}}$, что приводит к выходу ${ Displaystyle Z _ {(М раз N-1) + (К раз L-1)}}$. Это выражается следующим образом:

${ Displaystyle Z (я, j) ​​= сумма _ {м = 0} ^ {M-1} sum _ {n = 0} ^ {N-1} X (m, n) Y (im, jn) }$

Затем создаются две матрицы, которые заполняют каждый вход нулями в обоих измерениях, так что каждый вход имеет эквивалентные размеры, т.е.

${ displaystyle mathbf {X '} = { begin {bmatrix} X & 0 0 & 0 end {bmatrix}}}$ и ${ displaystyle mathbf {Y '} = { begin {bmatrix} Y & 0 0 & 0 end {bmatrix}}}$

где каждая из входных матриц теперь имеет размеры ${ Displaystyle (М + К-1)}$${ displaystyle times}$${ Displaystyle (N + L-1)}$. Затем можно реализовать лексикографическое упорядочение по столбцам, чтобы преобразовать модифицированные матрицы в векторы, ${ displaystyle X ''}$ и ${ displaystyle Y ''}$. Чтобы минимизировать количество неважных выборок в каждом векторе, каждый вектор усекается после последней выборки в исходных матрицах. ${ displaystyle X}$ и ${ displaystyle Y}$ соответственно. Учитывая это, длина вектора ${ displaystyle X ''}$ и ${ displaystyle Y ''}$ даны:

${ displaystyle l_ {X ''} =}$ ${ Displaystyle (М + К-1)}$${ displaystyle times}$${ Displaystyle (N-1)}$ + ${ displaystyle M}$

${ displaystyle l_ {Y ''} =}$${ Displaystyle (М + К-1)}$${ displaystyle times}$${ Displaystyle (L-1)}$ + ${ displaystyle K}$

Длина свертки этих двух векторов, ${ displaystyle Z ''}$, может быть получено и показано как:

${ displaystyle l_ {Z ''} =}$ ${ displaystyle l_ {Y ''} +}$${ displaystyle l_ {X ''}}$ ${ Displaystyle = (М + К-1)}$${ displaystyle times}$${ Displaystyle (N + L-1)}$

Длина этого вектора эквивалентна размерам исходной выходной матрицы. ${ displaystyle Z}$, что делает преобразование обратно в матрицу прямым преобразованием. Таким образом, вектор, ${ displaystyle Z ''}$, преобразуется обратно в матричную форму, которая дает результат двумерной дискретной свертки.^[14]

Фильтрация по спирали

При работе с двумерной декартовой сеткой преобразование Фурье по любой из осей приведет к тому, что двумерная плоскость станет цилиндром, поскольку конец каждого столбца или строки присоединяется к соответствующей вершине, образуя цилиндр. Фильтрация по спирали ведет себя аналогичным образом, за исключением того, что в этом случае нижняя часть каждого столбца присоединяется к верху следующего столбца, в результате чего получается спиральная сетка. Это проиллюстрировано ниже. Затемненные плитки представляют коэффициенты фильтра.

Если эту спиральную структуру затем разрезать и развернуть в одномерную полосу, те же коэффициенты фильтра на 2-мерной декартовой плоскости будут совпадать с теми же входными данными, что приведет к эквивалентной схеме фильтрации. Это гарантирует, что двумерная свертка сможет быть выполнена оператором одномерной свертки, поскольку двумерный фильтр был развернут в одномерный фильтр с пропусками нулей, разделяющими коэффициенты фильтра.

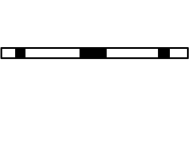
Предполагая, что использовался какой-то двухмерный фильтр нижних частот, например:

0	-1	0
-1	4	-1
0	-1	0

Затем, как только двумерное пространство было преобразовано в спираль, одномерный фильтр будет выглядеть следующим образом:

${ displaystyle h (n) = - 1,0, ..., 0, -1,4, -1,0, ..., 0, -1,0, ...}$

Обратите внимание на то, что в одномерном фильтре нет ведущих нулей, как показано на одномерной полосе фильтрации после разматывания. Всю одномерную полосу можно было бы свернуть; однако игнорировать начальные нули проще с точки зрения вычислений. Кроме того, ни одно из этих обратных нулевых значений не нужно хранить в памяти, что позволяет экономить драгоценные ресурсы памяти.^[15]

Приложения

Преобразования спирали для реализации рекурсивных фильтров посредством свертки используются в различных областях обработки сигналов. Хотя анализ Фурье в частотной области эффективен, когда системы являются стационарными, с постоянными коэффициентами и периодически дискретизируемыми данными, в нестабильных системах он становится более трудным. Преобразование спирали позволяет выполнять трехмерные процессы миграции после суммирования, которые могут обрабатывать данные для трехмерных изменений скорости.^[15] Кроме того, его можно применять для решения проблемы неявной экстраполяции трехмерного волнового поля.^[16] Другие приложения включают полезные алгоритмы регуляризации сейсмических данных, фильтры ошибок прогнозирования и ослабление шума в геофизических цифровых системах.^[14]

Гауссова свертка

Одно из применений многомерной свертки, которое используется при обработке сигналов и изображений, - это свертка по Гауссу. Это относится к свертке входного сигнала с функцией распределения Гаусса.

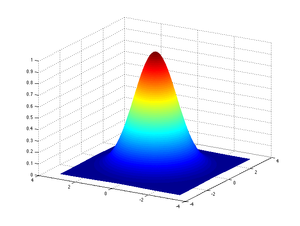
Распределение Гаусса, полученное с дискретными значениями в одном измерении, дается следующим образом (при условии, что ${ displaystyle mu = 0}$):

Это легко распространяется на сигнал M размеры (при условии ${ displaystyle sigma}$ остается неизменным для всех размеров и ${ displaystyle mu _ {1} = mu _ {2} = ... = mu _ {M} = 0}$):Следует признать одно важное свойство: M размерный сигнал разделим таким образом, что:Тогда свертка Гаусса с дискретными сигналами может быть выражена следующим образом:

${ Displaystyle у (п) = х (п) * г (п)}$

${ displaystyle y (n_ {1}, n_ {2}, ..., n_ {M}) = x (n_ {1}, n_ {2}, ..., n_ {M}) * ... * G (n_ {1}, n_ {2}, ..., n_ {M})}$

Аппроксимация КИХ-фильтром

Гауссова свертка может быть эффективно аппроксимирована с помощью реализации Конечный импульсный отклик (FIR) фильтр. Фильтр будет разработан с усеченными версиями Гаусса. Для двумерного фильтра передаточная функция такого фильтра будет определяться следующим образом:^[17]

${ displaystyle H (z_ {1}, z_ {2}) = { frac {1} {s (r_ {1}, r_ {2})}} sum _ {n_ {1} = - r_ {1 }} ^ {r_ {1}} sum _ {n_ {2} = - r_ {2}} ^ {r_ {2}} G (n_ {1}, n_ {2}) {z_ {1}} ^ {-n_ {1}} {z_ {2}} ^ {- n_ {2}}}$

куда

${ displaystyle s (r_ {1}, r_ {2}) = sum _ {n_ {1} = - r_ {1}} ^ {r_ {1}} sum _ {n_ {2} = - r_ { 2}} ^ {r_ {2}} G (n_ {1}, n_ {2})}$

Выбор более низких значений для ${ displaystyle r_ {1}}$ и ${ displaystyle r_ {2}}$ приведет к выполнению меньшего количества вычислений, но даст менее точное приближение, в то время как выбор более высоких значений даст более точное приближение, но потребует большего количества вычислений.

Аппроксимация коробчатым фильтром

Другой метод аппроксимации гауссовой свертки - это рекурсивные проходы через блочный фильтр. Для аппроксимации одномерной свертки этот фильтр определяется следующим образом:^[17]

${ displaystyle H (z) = { frac {1} {2r + 1}} { frac {z ^ {r} -z ^ {- r-1}} {1-z ^ {-} 1}} }$

Обычно рекурсивные проходы выполняются 3, 4 или 5 раз, чтобы получить точное приближение.^[17] Предлагаемый метод расчета р тогда дается как следующее:^[18]

${ displaystyle sigma ^ {2} = { frac {1} {12}} K ((2r + 1) ^ {2} -1)}$ куда K - количество рекурсивных проходов через фильтр.

Затем, поскольку распределение Гаусса разделяется по разным измерениям, из этого следует, что рекурсивные проходы через одномерные фильтры (изолирующие каждое измерение отдельно), таким образом, приведут к приближению многомерной свертки Гаусса. То есть, М-мерная гауссова свертка может быть аппроксимирована рекурсивными проходами через следующие одномерные фильтры:

${ displaystyle H (z_ {1}) = { frac {1} {2r_ {1} +1}} { frac {{z_ {1}} ^ {r_ {1}} - {z_ {1}} ^ {- r_ {1} -1}} {1- {z_ {1}} ^ {-} 1}}}$

${ displaystyle H (z_ {2}) = { frac {1} {2r_ {2} +1}} { frac {{z_ {2}} ^ {r_ {2}} - {z_ {2}} ^ {- r_ {2} -1}} {1- {z_ {2}} ^ {-} 1}}}$

${ displaystyle vdots}$

${ displaystyle H (z_ {M}) = { frac {1} {2r_ {M} +1}} { frac {{z_ {M}} ^ {r_ {M}} - {z_ {M}} ^ {- r_ {M} -1}} {1- {z_ {M}} ^ {-} 1}}}$

Приложения

Гауссовы свертки широко используются при обработке сигналов и изображений. Например, размытие изображения может быть выполнено с помощью гауссовой свертки, где ${ displaystyle sigma}$ Параметр будет контролировать силу размытия. Таким образом, более высокие значения будут соответствовать более размытому конечному результату.^[19] Он также обычно используется в Компьютерное зрение такие приложения, как Масштабно-инвариантное преобразование признаков (SIFT) обнаружение функции.^[20]

Смотрите также

• Свертка
• Обработка изображений
• Обработка сигналов

Рекомендации