Конструкция Powerset - Powerset construction

в теория вычислений и теория автоматов, то конструкция электростанции или же конструкция подмножества стандартный метод для преобразование а недетерминированный конечный автомат (NFA) в детерминированный конечный автомат (DFA), который распознает то же формальный язык. Это важно в теории, поскольку устанавливает, что NFA, несмотря на их дополнительную гибкость, не могут распознавать любой язык, который не может быть распознан некоторыми DFA. Это также важно на практике для преобразования простых в создании NFA в более эффективно выполняемые DFA. Однако если в NFA п утверждает, что в итоговом DFA может быть до 2п состояний, экспоненциально большее число, что иногда делает конструкцию непрактичной для больших NFA.

Конструкция, которую иногда называют Конструкция электростанции Рабина – Скотта (или конструкция подмножества), чтобы отличать ее от аналогичных конструкций для других типов автоматов, была впервые опубликована Майкл О. Рабин и Дана Скотт в 1959 г.[1]

Интуиция

Чтобы смоделировать работу DFA с заданной входной строкой, необходимо отслеживать одно состояние в любое время: состояние, которого автомат достигнет после просмотра префикс входа. Напротив, для моделирования NFA необходимо отслеживать набор состояний: все состояния, которые автомат может достичь после просмотра одного и того же префикса ввода, в соответствии с недетерминированным выбором, сделанным автоматом. Если после определенного префикса ввода установлен S состояний может быть достигнуто, то после следующего входного символа Икс набор достижимых состояний является детерминированной функцией S и Икс. Следовательно, наборы достижимых состояний NFA играют ту же роль в моделировании NFA, что и отдельные состояния DFA в моделировании DFA, и на самом деле наборы состояний NFA, появляющиеся в этой симуляции, могут быть повторно интерпретированы как состояния DFA.[2]

Строительство

Конструкция powerset наиболее непосредственно применима к NFA, которая не допускает преобразования состояний без использования входных символов (также известных как «ε-ходы»). Такой автомат можно определить как 5-кратный (Q, Σ, Т, q0, F), в котором Q это множество состояний, Σ - набор входных символов, Т - функция перехода (отображение состояния и входного символа в набор состояний), q0 - начальное состояние, а F - набор принимающих состояний. Соответствующий DFA имеет состояния, соответствующие подмножествам Q. Начальное состояние DFA: {q0}, (одноэлементный) набор начальных состояний. Функция перехода DFA отображает состояние S (представляет собой подмножество Q) и входной символ Икс к набору Т(S,Икс) = ∪{Т(q,Икс) | q ∈ S}, множество всех состояний, в которые может попасть Икс-переход из состояния в S.Штат S DFA является принимающим государством тогда и только тогда, когда хотя бы один член S является принимающим государством NFA.[2][3]

В простейшем варианте конструкции powerset набор всех состояний DFA является powerset из Q, множество всех возможных подмножеств Q. Однако многие состояния результирующего DFA могут оказаться бесполезными, поскольку они могут быть недоступны из начального состояния. Альтернативный вариант конструкции создает только реально достижимые состояния.[4]

NFA с ε-ходами

Для NFA с ε-движениями (также называемых ε-NFA) конструкция должна быть изменена, чтобы справиться с ними путем вычисления ε-закрытие состояний: множество всех состояний, достижимых из некоторого заданного состояния с использованием только ε-ходов. Ван Норд выделяет три возможных способа включения этого вычисления замыкания в конструкцию powerset:[5]

  1. Вычислите ε-замыкание всего автомата как шаг предварительной обработки, создав эквивалентный NFA без ε-ходов, а затем примените обычную конструкцию powerset. Эта версия, также обсуждаемая Хопкрофтом и Ульманом,[6] прост в реализации, но непрактичен для автоматов с большим числом ε-ходов, как это обычно бывает в обработка естественного языка заявление.[5]
  2. Во время вычисления powerset вычислите ε-замыкание каждого государства q который учитывается алгоритмом (и кеширует результат).
  3. Во время вычисления powerset вычислите ε-замыкание каждого подмножества состояний Q ' который учитывается алгоритмом, и добавляют его элементы в Q '.

Несколько начальных состояний

Если NFA определены с учетом нескольких начальных состояний,[7] начальное состояние соответствующего DFA - это множество всех начальных состояний NFA или (если NFA также имеет ε-ходы) набор всех состояний, достижимых из начальных состояний с помощью ε-ходов.

Пример

NFA ниже имеет четыре состояния; состояние 1 является начальным, а состояния 3 и 4 - допустимыми. Его алфавит состоит из двух символов 0 и 1 и имеет ε-ходы.

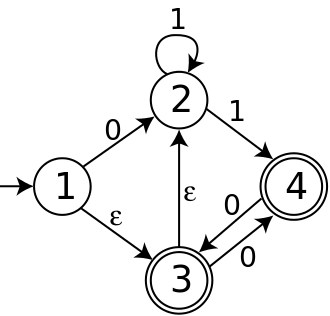
NFA-powerset-construction-example.svg

Начальное состояние DFA, построенного из этой NFA, представляет собой набор всех состояний NFA, которые достижимы из состояния 1 с помощью ε-ходов; то есть это набор {1,2,3}. Переход от {1,2,3} входным символом 0 должен следовать либо за стрелкой из состояния 1 в состояние 2, либо за стрелкой из состояния 3 в состояние 4 Кроме того, ни состояние 2, ни состояние 4 не имеют исходящих ε-перемещений. Следовательно, Т({1,2,3}, 0) = {2,4}, и по тем же соображениям полный DFA, созданный из NFA, показан ниже.

DFA-powerset-construction-example.svg

Как видно из этого примера, есть пять состояний, достижимых из начального состояния DFA; остальные 11 наборов в наборе мощности набора состояний NFA недостижимы.

Сложность

Основная статья: Сложность состояния
NFA с 5 состояниями (слева), для DFA (справа) требуется 16 состояний.[4]

Поскольку состояния DFA состоят из наборов состояний NFA, п-state NFA может быть преобразован в DFA с не более чем 2п состояния.[2] Для каждого п, существуют п-состояния NFA такие, что каждое подмножество состояний достижимо из начального подмножества, так что преобразованный DFA имеет точно 2п состояний, давая Θ (2п) худший случай временная сложность.[8][9] Простым примером, требующим почти такого количества состояний, является язык строк в алфавите {0,1}, в котором не менее п персонажи, пth от последнего из которых 1. Это может быть представлено (п + 1)-state NFA, но требует 2п Состояния DFA, по одному для каждого п-суффикс символа ввода; ср. картина для п=4.[4]

Приложения

Алгоритм Бжозовского для минимизации DFA использует конструкцию powerset дважды. Он преобразует входной DFA в NFA для обратного языка, переворачивая все его стрелки и меняя роли начального и принимающего состояний, преобразует NFA обратно в DFA, используя конструкцию powerset, а затем повторяет свой процесс. Его сложность наихудшего случая является экспоненциальной, в отличие от некоторых других известных алгоритмов минимизации DFA, но во многих примерах он работает быстрее, чем можно было бы предположить по сложности наихудшего случая.[10]

Строительство Сафры, который преобразует недетерминированный Büchi автомат с п государства в детерминированный Автомат Мюллера или в детерминированный Автомат Рабина с 2O (п бревно п) государства, использует конструкцию силового агрегата как часть своего оборудования.[11]

Рекомендации

  1. ^ Рабин, М.О.; Скотт, Д. (1959). «Конечные автоматы и проблемы их решения». Журнал исследований и разработок IBM. 3 (2): 114–125. Дои:10.1147 / rd.32.0114. ISSN  0018-8646.
  2. ^ а б c Сипсер, Майкл. «Теорема 1.19». Введение в теорию вычислений. стр.55–56. ISBN  0-534-94728-X.
  3. ^ Хопкрофт, Джон Э.; Ульман, Джеффри Д. (1979). «Эквивалентность DFA и NFA». Введение в теорию автоматов, языки и вычисления. Чтение Массачусетса: Эддисон-Уэсли. стр.22–23. ISBN  0-201-02988-X.CS1 maint: ref = harv (связь)
  4. ^ а б c Шнайдер, Клаус (2004). Верификация реактивных систем: формальные методы и алгоритмы. Springer. С. 210–212. ISBN  978-3-540-00296-3.
  5. ^ а б Ван Норд, Гертян (2000). «Обработка эпсилон-движений в построении подмножеств». Компьютерная лингвистика. 26 (1): 61–76. arXiv:cmp-lg / 9804003. Дои:10.1162/089120100561638.
  6. ^ Хопкрофт и Ульман (1979) С. 26–27.
  7. ^ Роте, Йорг (2006). Теория сложности и криптология: введение в криптосложность. Тексты по теоретической информатике. Springer. С. 21–22. ISBN  9783540285205..
  8. ^ Лупанов, Олег Б. (1963). «Сравнение двух типов конечных источников». Проблемы Кибернетики. 9: 321–326.
  9. ^ Мур, Фрэнк Р. (1971). «О границах размера множества состояний в доказательствах эквивалентности детерминированных, недетерминированных и двусторонних конечных автоматов». Транзакции IEEE на компьютерах. С-20 (10): 1211–1214. Дои:10.1109 / T-C.1971.223108..
  10. ^ Бжозовский, Ю.А. (1963). «Канонические регулярные выражения и минимальные графы состояний для определенных событий». Proc. Симпози. Математика. Теория автоматов (Нью-Йорк, 1962). Политехническая пресса Политехнического института. of Brooklyn, Brooklyn, N.Y., стр. 529–561. МИСТЕР  0175719.
  11. ^ Сафра, С. (1988). «О сложности ω-автоматов». Материалы 29-го ежегодного Симпозиум по основам информатики (FOCS '88). Вашингтон, округ Колумбия, США: Компьютерное общество IEEE. С. 319–327. Дои:10.1109 / SFCS.1988.21948..

дальнейшее чтение