Производственная эффективность - Productive efficiency

Пример PPF: все точки B, C и D производительно эффективны, но экономика в точке A не будет такой, потому что D предполагает большее производство обоих товаров. Точка X не может быть достигнута.
Производственная эффективность достигается при конкурентном равновесии при минимуме средней общей стоимости каждого товара, такого как показано здесь.

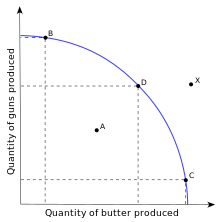
Производственная эффективность (или эффективность производства) - это ситуация, в которой экономия или экономическая система (например, фирма, банк, больница, отрасль, страна и т. д.) не могла производить больше одного товара без ущерба для производства другого товара и без улучшения технологии производства.[1] Другими словами, продуктивная эффективность достигается, когда товар или услуга производятся с наименьшими возможными затратами. Проще говоря, концепция проиллюстрирована на граница производственных возможностей (PPF), где все точки на кривой являются точками производственной эффективности.[2] Равновесие может быть продуктивно эффективным, но не распределительно эффективный - т.е. это может привести к распределению товаров, где социальное обеспечение не разворачивается. Это один из видов экономическая эффективность.

Производственная эффективность отрасли требует, чтобы все фирмы работали с использованием передовых технологических и управленческих процессов и чтобы не было дальнейшего перераспределения, которое привело бы к увеличению выпуска при тех же затратах и ​​тех же производственных технологиях. Улучшая эти процессы, экономия или бизнес может продлить граница производственных возможностей наружу, так что эффективное производство дает больше продукции, чем раньше.

Производственная неэффективность, когда экономика работает ниже границы своих производственных возможностей, может возникнуть из-за того, что производственные ресурсы физический капитал рабочая сила используется в недостаточной степени - то есть часть капитала или рабочей силы остается бездействующей - или потому, что эти ресурсы распределяются в несоответствующих комбинациях различным отраслям, которые их используют.

В долгосрочное равновесие для совершенно конкурентных рынков продуктивная эффективность достигается на база из кривая средних общих затрат —Т.е. где предельные затраты равны средней общей стоимости каждого товара.

Из-за характера и культуры компаний-монополистов они могут быть неэффективными из-за Х-неэффективность, в результате чего компании, работающие в условиях монополии, имеют меньше стимулов для максимизации выпуска из-за отсутствия конкуренции. Однако из-за эффекта масштаба может быть возможным, чтобы уровень производства компаний-монополистов, максимизирующий прибыль, был достигнут при более низкой цене для потребителя, чем у компаний с идеальной конкуренцией.

В литературе было предложено много теоретических мер эффективности производства, а также множество подходов к их оценке. Наиболее популярные меры эффективности включают меру Фаррелла.[3] (также известная как мера Дебре-Фаррелла, поскольку у Дебреу (1951) похожие идеи[4]). Эта мера также является обратной функцией расстояния Шепарда.[5]Они могут быть определены либо с ориентацией входа (зафиксировать выходы и измерить максимально возможное сокращение входов), либо с ориентацией выхода (зафиксировать входы и измерить максимально возможное расширение выходов). Их обобщением является так называемая функция направленного расстояния, в которой можно выбрать любое направление (или ориентацию) для измерения эффективности производства. Наиболее популярными для оценки эффективности производства являются: Анализ охвата данных[6] и Стохастический пограничный анализ [7], среди других методов. (Например, см. Недавнюю книгу Сиклза и Зеленюка (2019) для всестороннего освещения теории и связанных с ней оценок, а также многих ссылок в ней.)[8]

Рекомендации

  1. ^ Сиклз, Р., Зеленюк, В. (2019). Измерение производительности и эффективности: теория и практика. Кембридж: Издательство Кембриджского университета. DOI: 10.1017 / 9781139565981
  2. ^ Стэндиш, Барри (1997). Экономика: принципы и практика. Южная Африка: Pearson Education. С. 13–15. ISBN  978-1-86891-069-4.
  3. ^ Фаррелл, М. Дж. (1957). Измерение производственной эффективности. Журналь Королевского статистического общества. Серия А (Общие), 120 (3): 253–290.
  4. ^ Дебре, Г. (1951). Коэффициент использования ресурса. Econometrica, 19 (3): 273–292.
  5. ^ Шепард, Р. В. (1953). Стоимость и производственные функции. Принстон, Нью-Джерси: Издательство Принстонского университета.
  6. ^ Чарнс, А., Купер, В., и Родс, Э. (1978). Измерение эффективности единиц принятия решений. Европейский журнал операционных исследований, 2 (6): 429–444.
  7. ^ Эйгнер, Д. Дж., Ловелл, К. А. К. и Шмидт, П. (1977), «Формулировка и оценка стохастических граничных производственных функций», Journal of Econometrics 6 (1), 21–37.
  8. ^ Сиклз, Р., Зеленюк, В. (2019). Измерение производительности и эффективности: теория и практика. Кембридж: Издательство Кембриджского университета. DOI: 10.1017 / 9781139565981