Quickhull - Википедия - Quickhull

Quickhull это метод вычисления выпуклый корпус конечного множества точек в п-мерное пространство. Он использует разделяй и властвуй подход, аналогичный подходу быстрая сортировка, от которого и произошло его название. Его сложность наихудшего случая для 2-мерного и 3-мерного пространства считается равной ${ Displaystyle О (п журнал (г))}$, куда ${ displaystyle n}$ количество входных точек и ${ displaystyle r}$ количество обработанных точек^[1]. Однако, в отличие от быстрой сортировки, нет очевидного способа преобразовать quickhull в рандомизированный алгоритм. Тем не менее, есть работы от Сглаженный анализ которые говорят нам, что двумерный алгоритм Quick Hull ожидает время выполнения ${ Displaystyle О (п журнал (п))}$. В самом деле, ^[2] и связанные с ним работы показывают, что количество точек на выпуклой оболочке любого случайно возмущенного набора точек с гауссовым шумом равно ${ Displaystyle О ({ sqrt { log n}})}$ из чего следует, что Quick Hull (и многие другие алгоритмы) могут занимать только время ${ Displaystyle О (п { sqrt { log n}})}$ на любом множестве возмущенных точек.

N-мерный Quickhull был изобретен в 1996 году К. Брэдфордом Барбером, Дэвид П. Добкин и Ханну Хухданпаа.^[1] Это было расширение планарного алгоритма Quickhull Джонатана Скотта Гринфилда 1990 года, хотя авторы 1996 года не знали о его методах.^[3] Вместо этого Барбер и др. Описывают его как детерминированный вариант алгоритма Кларксона и Шора 1989 года.^[1]

На этой анимации изображен алгоритм quickhull.

Алгоритм

Шаги 1-2: разделите очки на два подмножества

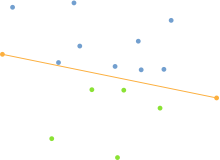
В обычных условиях алгоритм работает достаточно хорошо, но обработка обычно замедляется в случаях высокой симметрии или точек, лежащих на окружности круга. Алгоритм можно разбить на следующие этапы:^[3]

1. Найдите точки с минимальными и максимальными координатами x, так как они всегда будут частью выпуклой оболочки. Если существует много точек с одинаковым минимальным / максимальным x, используйте соответственно точки с минимальным / максимальным y.
2. Используйте линию, образованную двумя точками, чтобы разделить набор на два подмножества точек, которые будут обрабатываться рекурсивно.
3. Определите точку на одной стороне линии на максимальном расстоянии от линии. Эта точка образует треугольник с точками линии.
4. Точки, лежащие внутри этого треугольника, не могут быть частью выпуклой оболочки и, следовательно, могут быть проигнорированы на следующих шагах.
5. Повторите предыдущие два шага на двух линиях, образованных треугольником (не на исходной линии).
6. Продолжайте делать это до тех пор, пока не останется больше точек, рекурсия не закончится и выбранные точки не образуют выпуклую оболочку.

Шаги 3-5: Найдите точку максимального расстояния, игнорируйте точки внутри треугольника и повторите это

Шаг 6: повторяйте, пока не кончатся баллы

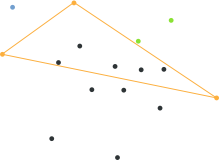
Проблема более сложна в многомерном случае, поскольку корпус состоит из множества граней; структура данных должна учитывать это и записывать линию / плоскость / гиперплоскость (гребень), общие для соседних фасетов. За d размеры:^[1]

1. Выбирать d +1 очко из набора, не имеющего общей плоскости или гиперплоскости. Это формирует начальный корпус с гранями. Fs [].
2. Для каждого F в Fs [], найдите все неназначенные точки, которые находятся "над" ним, то есть указывающие от центра корпуса, и добавьте их в "внешний" набор F.O связана с F.
3. Для каждого F с непустым F.O:
   1. Найдите точку п с максимальным удалением от F. Мы добавим его в корпус.
   2. Создайте видимый набор V и инициализировать его F. Продлевать V во все стороны для соседних граней Fv пока не исчезнут другие грани п. Fv быть видимым из п Значит это п выше Fv
   3. Граница V затем формирует набор гребней горизонта ЧАС.
   4. Позволять Fnew [] быть набором граней, созданных из п и все гребни в ЧАС.
   5. Для каждой новой грани в Fnew [], выполните шаг (2) и инициализируйте свои собственные внешние наборы. На этот раз смотрите только с точек, которые находятся вне грани в V используя свои внешние наборы V [i] .O, поскольку мы только расширились в этом направлении.
   6. Удалите теперь внутренние фасеты в V из Fs []. Добавьте новые грани в Fnew [] к Fs [] и продолжаем итерацию.

Псевдокод для двухмерного набора точек

Вход = набор S из n точек Предположим, что есть не менее 2 точек во входном наборе S точекфункция QuickHull (S) является    // Находим выпуклую оболочку из множества S из n точек    Выпуклая оболочка: = {} Найдите крайние левые и правые точки, скажем A и B, и добавьте A и B к выпуклой оболочке. Сегмент AB делит оставшиеся (п - 2) балла на 2 группы S1 и S2         куда S1 точки в S которые находятся справа от ориентированной линии от А к B,         и S2 точки в S которые находятся справа от ориентированной линии от B к А     FindHull (S1, А, B) FindHull (S2, B, А) Выход: = Выпуклая оболочкаконечная функцияфункция FindHull (Sk, п, Q) является    // Находим точки на выпуклой оболочке из множества точек Sk     // которые находятся справа от ориентированной прямой от P до Q    если Sk не имеет смысла тогда        возвращаться    Из заданного набора точек в Sk, найди самую дальнюю точку, скажи C, из сегмента PQ     Добавить точку C к выпуклой оболочке в месте между п и Q     Три балла п, Q, и C разделить оставшиеся точки Sk на 3 подмножества: S0, S1, и S2         куда S0 точки внутри треугольника PCQ, S1 - точки справа от ориентированной прямой от п к C, и S2 - точки справа от ориентированной прямой от C к Q. FindHull (S1, п, C) FindHull (S2, C, Q) конечная функция

Псевдокод, специализированный для трехмерного случая, можно получить у Джордана Смита. Он включает аналогичную стратегию «максимальной точки» для выбора начального корпуса. Если эти максимальные точки вырождены, все облако точек тоже.^[4]

Смотрите также

• Алгоритмы выпуклой оболочки

Рекомендации

• Дэйв Маунт. «Лекция 3: Больше алгоритмов выпуклой оболочки».
• Псевдокод, "http://www.cse.yorku.ca/~aaw/Hang/quick_hull/Algorithm.html ".

внешняя ссылка

• Внедрение QuickHull (GDC 2014) - Представление алгоритма с подробностями реализации в 3D.