Граф Робертсона – Вегнера - Robertson–Wegner graph
| Граф Робертсона – Вегнера | |
|---|---|
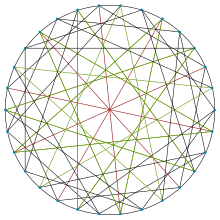 | |
| Названный в честь | Нил Робертсон |
| Вершины | 30 |
| Края | 75 |
| Радиус | 3 |
| Диаметр | 3 |
| Обхват | 5 |
| Автоморфизмы | 20 |
| Хроматическое число | 4 |
| Хроматический индекс | 5[1] |
| Характеристики | Клетка |
| Таблица графиков и параметров | |
в математический поле теория графов, то Граф Робертсона – Вегнера это 5-обычный неориентированный граф с 30 вершинами и 75 ребрами, названными в честь Нил Робертсон и Г. Вегнер.[2][3][4]
Это один из четырех (5,5) -клеточные графики, остальные Приемная клетка, то Граф Мерингера, а Граф Вонга.
Она имеет хроматическое число 4, диаметр 3, и 5-вершинно-связанный.
Алгебраические свойства
В характеристический многочлен графа Робертсона – Вегнера есть
Рекомендации
- ^ Вайсштейн, Эрик В. "График 2 класса". MathWorld.
- ^ Вайсштейн, Эрик В. «График Робертсона – Вегнера». MathWorld.
- ^ Бонди, Дж. А., Мёрти, США. Теория графов с приложениями. Нью-Йорк: Северная Голландия, стр. 238, 1976.
- ^ Вонг, П. К. «Заметка к статье Г. Вегнера», Journal of Combinatorial Theory, Series B, 22: 3, июнь 1977 г., стр. 302-303, doi: 10.1016 / 0095-8956 (77) 90081-8

