Правило смесей - Rule of mixtures

Верхняя и нижняя границы модуля упругости композиционного материала, как предсказывается правилом смесей. Фактический модуль упругости находится между кривыми.

В материаловедение, а общее правило смесей это средневзвешенное значение используется для прогнозирования различных свойств композитный материал состоит из непрерывных и однонаправленных волокон.^[1][2][3] Он обеспечивает теоретическую верхнюю и нижнюю границу таких свойств, как модуль упругости, плотность вещества, предел прочности на растяжение, теплопроводность, и электрическая проводимость.^[3] В общем, есть две модели, одна для осевой нагрузки (модель Фойгта),^[2][4] и один для поперечной нагрузки (модель Рейсса).^[2][5]

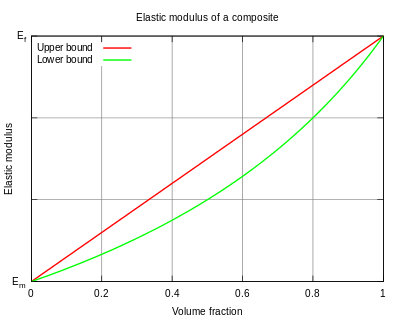
В общем, по некоторому материальному свойству ${ displaystyle E}$ (часто модуль упругости^[1]), правило смесей гласит, что общее свойство в направлении, параллельном волокнам, может достигать

${ displaystyle E_ {c} = fE_ {f} + left (1-f right) E_ {m}}$

куда

• ${ displaystyle f = { frac {V_ {f}} {V_ {f} + V_ {m}}}}$ это объемная доля волокон
• ${ displaystyle E_ {f}}$ это свойство материала волокон
• ${ displaystyle E_ {m}}$ материальное свойство матрицы

В случае модуля упругости это известно как модуль верхней границы, и соответствует нагрузке, параллельной волокнам. В обратное правило смесей утверждает, что в направлении, перпендикулярном волокнам, модуль упругости композита может быть таким низким, как

${ displaystyle E_ {c} = left ({ frac {f} {E_ {f}}} + { frac {1-f} {E_ {m}}} right) ^ {- 1}.}$

Если исследуемым свойством является модуль упругости, эта величина называется величиной модуль нижней границы, и соответствует поперечной нагрузке.^[2]

Вывод для модуля упругости

Модуль верхней границы

Рассмотрим композитный материал под одноосное растяжение ${ displaystyle sigma _ { infty}}$. Если материал должен оставаться нетронутым, напряжение волокон, ${ displaystyle epsilon _ {f}}$ должно равняться деформации матрицы, ${ displaystyle epsilon _ {m}}$. Закон Гука для одноосного растяжения, следовательно, дает

${ displaystyle { frac { sigma _ {f}} {E_ {f}}} = epsilon _ {f} = epsilon _ {m} = { frac { sigma _ {m}} {E_ { m}}}}$

(1)

куда ${ displaystyle sigma _ {f}}$, ${ displaystyle E_ {f}}$, ${ displaystyle sigma _ {m}}$, ${ displaystyle E_ {m}}$ - напряжение и модуль упругости волокон и матрицы соответственно. Учитывая, что напряжение - это сила на единицу площади, баланс сил дает

${ displaystyle sigma _ { infty} = е sigma _ {f} + влево (1-е вправо) sigma _ {m}}$

(2)

куда ${ displaystyle f}$ - объемная доля волокон в композите (и ${ displaystyle 1-f}$ - объемная доля матрицы).

Если предположить, что композитный материал ведет себя как линейно-упругий материал, т. Е. Подчиняется закону Гука ${ displaystyle sigma _ { infty} = E_ {c} epsilon _ {c}}$ для некоторого модуля упругости композита ${ displaystyle E_ {c}}$ и некоторая деформация композита ${ displaystyle epsilon _ {c}}$, то уравнения 1 и 2 можно объединить, чтобы дать

${ displaystyle E_ {c} epsilon _ {c} = fE_ {f} epsilon _ {f} + left (1-f right) E_ {m} epsilon _ {m}.}$

Наконец, поскольку ${ displaystyle epsilon _ {c} = epsilon _ {f} = epsilon _ {m}}$, общий модуль упругости композита можно выразить как^[6]

${ displaystyle E_ {c} = fE_ {f} + left (1-f right) E_ {m}.}$

Модуль нижней границы

Теперь пусть композитный материал загружен перпендикулярно волокнам, предполагая, что ${ displaystyle sigma _ { infty} = sigma _ {f} = sigma _ {m}}$. Общая деформация в композите распределяется между материалами так, что

${ displaystyle epsilon _ {c} = f epsilon _ {f} + left (1-f right) epsilon _ {m}.}$

Общий модуль упругости материала тогда определяется как

${ displaystyle E_ {c} = { frac { sigma _ { infty}} { epsilon _ {c}}} = { frac { sigma _ {f}} {f epsilon _ {f} + left (1-f right) epsilon _ {m}}} = left ({ frac {f} {E_ {f}}} + { frac {1-f} {E_ {m}}} right) ^ {- 1}}$

поскольку ${ displaystyle sigma _ {f} = E epsilon _ {f}}$, ${ displaystyle sigma _ {m} = E epsilon _ {m}}$.^[6]

Другие свойства

Подобные выводы дают правила смесей для

• плотность вещества

${ displaystyle left ({ frac {f} { rho _ {f}}} + { frac {1-f} { rho _ {m}}} right) ^ {- 1} leq rho _ {c} leq f rho _ {f} + left (1-f right) rho _ {m}}$

• предел прочности на растяжение

${ displaystyle left ({ frac {f} { sigma _ {UTS, f}}} + { frac {1-f} { sigma _ {UTS, m}}} ​​ right) ^ {- 1 } leq sigma _ {UTS, c} leq f sigma _ {UTS, f} + left (1-f right) sigma _ {UTS, m}}$

• теплопроводность

${ displaystyle left ({ frac {f} {k_ {f}}} + { frac {1-f} {k_ {m}}} right) ^ {- 1} leq k_ {c} leq fk_ {f} + left (1-f right) k_ {m}}$

• электрическая проводимость

${ displaystyle left ({ frac {f} { sigma _ {f}}} + { frac {1-f} { sigma _ {m}}} right) ^ {- 1} leq сигма _ {c} leq f sigma _ {f} + left (1-f right) sigma _ {m}}$

Смотрите также

При рассмотрении эмпирической корреляции некоторых физических свойств и химического состава соединений другие соотношения, правила или законы также очень напоминают правило смесей:

• Закон Амагата - Закон парциальных объемов газов
• Уравнение Гладстона – Дейла - Оптический анализ жидкостей, стекол и кристаллов
• Закон Коппа - Использует массовая доля
• Закон Коппа – Неймана - Удельная теплоемкость сплавов
• Закон Вегарда - Параметры кристаллической решетки

Рекомендации

внешняя ссылка

• Калькулятор правил смесей