Сейсмическая интерферометрия - Seismic interferometry

Интерферометрия исследует общие явления интерференции между парами сигналов, чтобы получить полезную информацию о геологической среде.[1] Сейсмическая интерферометрия (SI) использует взаимная корреляция пар сигналов для восстановления импульсной характеристики данной среды. Статьи Кейити Аки (1957),[2] Геза Кунец и Джон Клаербут (1968)[3] помог разработать технику для сейсмический приложений и обеспечил основу, на которой основана современная теория.

Сигнал в местоположении A может быть коррелирован с сигналом в местоположении B, чтобы воспроизвести виртуальную пару источник-приемник с использованием сейсмической интерферометрии. Взаимная корреляция часто считается ключевой математической операцией в этом подходе, но также можно использовать свертка придумать аналогичный результат. Кросс-корреляция пассивного шума, измеренного на свободной поверхности, воспроизводит подповерхностный импульсный отклик. Таким образом, можно получить информацию о недрах без необходимости в активном сейсмический источник.[4] Однако этот метод не ограничивается пассивными источниками и может быть расширен для использования с активные источники и компьютерные формы волны.[1]

Изображение, показывающее полезность сейсмических волн для исследования недр.

С 2006 года в области сейсмической интерферометрии начали меняться геофизики Посмотреть сейсмический шум. Сейсмическая интерферометрия использует это ранее игнорировавшееся фоновое волновое поле, чтобы предоставить новую информацию, которая может быть использована для построения моделей геологической среды в качестве обратная задача. Возможные области применения варьируются от масштабов континента до более мелких стихийных бедствий, промышленных и экологических приложений.[1]

История и развитие

Claerbout (1968) разработали рабочий процесс для применения существующих методов интерферометрии для исследования неглубоких подповерхностных слоев, хотя позже не было доказано, что сейсмическая интерферометрия может применяться к средам реального мира.[1][5] Долгосрочное среднее значение случайный УЗИ волны могут восстановить импульсную характеристику между двумя точками на алюминий блокировать. Однако они предположили случайный диффузный шум, ограничивающий интерферометрию в реальных условиях. В аналогичном случае было показано, что выражения для некоррелированных источников шума сводятся к единой взаимной корреляции наблюдений на двух приемниках. Интерферометрический импульсный отклик геологической среды может быть восстановлен с использованием только расширенной записи фонового шума, первоначально только для поверхностных и прямых волн.[6][7]

Взаимная корреляция сейсмических сигналов как от активных, так и от пассивных источников на поверхности или в геологической среде может быть использована для восстановления достоверной модели геологической среды.[8] Сейсмическая интерферометрия может дать результат, аналогичный традиционным методам, без ограничений на коэффициент диффузии волнового поля или окружающих источников. В приложении для бурения можно использовать виртуальный источник для получения изображения геологической среды, прилегающей к скважине. Это приложение все чаще используется, в частности, для исследования подсолевых отложений.[9]

Математическое и физическое объяснение

Сейсмическая интерферометрия обеспечивает возможность восстановления отклика подземного отражения с использованием кросс-корреляций двух сейсмических трасс.[1][4] Недавняя работа[10] математически продемонстрировал применение кросс-корреляции для восстановления Функция Грина используя теорему взаимности волнового поля в трехмерной неоднородной среде без потерь. Трассы чаще всего представляют собой расширенные записи пассивного фонового шума, но также можно использовать активные источники в зависимости от цели. Сейсмическая интерферометрия по существу использует разность фаз между соседними местоположениями приемников для получения изображения геологической среды.

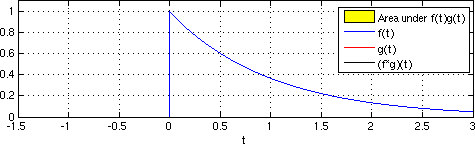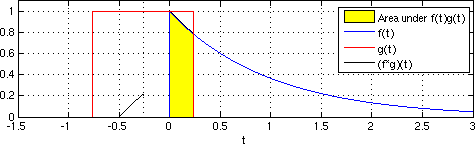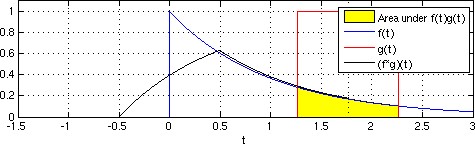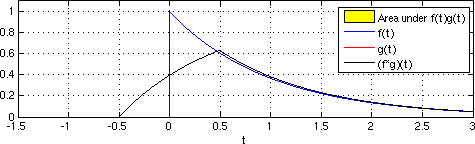
Сейсмическая интерферометрия состоит из простой кросс-корреляции и суммирования реальных откликов приемника для аппроксимации импульсной характеристики, как если бы виртуальный источник был размещен в месте расположения соответствующего приемника.[1] Взаимная корреляция непрерывных функций во временной области представлена ​​уравнением 1.

Уравнение 1

(f 1 ∗ f 2) (t) = ∫ f 1 (λ) f 2 (λ-t) dλ

Где функции интегрированы как функция времени при различных значениях запаздывания. Фактически, кросс-корреляцию можно концептуально понимать как задержку времени пробега, связанную с формами сигналов в двух дискретных местоположениях приемников. Кросс-корреляция похожа на свертку, где вторая функция сворачивается относительно первой.[11]

Сейсмическая интерферометрия принципиально похожа на оптическая интерферограмма создается интерференцией прямой и отраженной волн, проходящих через стеклянную линзу, где интенсивность в основном зависит от фазовой составляющей.

Принцип свертки. Аналогично взаимной корреляции

Уравнение 2

I = 1 + 2R2 cos [ω (λAr + λrB)] + R ^ 4

Где: Интенсивность связана с величиной коэффициента отражения (R) и фазовой составляющей ω (λAr + λrB).[4][10] Оценка распределений отражательной способности может быть получена посредством взаимной корреляции прямой волны в точке A с отражением, записанным в точке B, где A представляет собой опорную трассу.[8] Умножение конъюгата спектра следов в точке A и спектра следов в точке B дает:

Уравнение 3

ФAB = Re ^ iω (λAr + λrB) + o.t.

Где: ФAB = спектр продукта. = дополнительные условия, например корреляции прямое-прямое,[требуется разъяснение ] и т.д. Как и в предыдущем случае, спектр продукта является функцией фазы.

Ключ: Изменения в геометрии отражателя приводят к изменению результата корреляции, и геометрия отражателя может быть восстановлена ​​с помощью применения ядра миграции.[1][8] Интерпретация исходных интерферограмм обычно не предпринимается; кросс-коррелированные результаты обычно обрабатываются с использованием некоторой формы миграции.[8]

В простейшем случае рассмотрим вращающийся сверло на глубине излучающая энергия, регистрируемая геофоны на поверхности. Можно предположить, что фаза исходного вейвлета в данном положении случайна, и использовать кросс-корреляцию прямой волны в местоположении A с призрачным отражением в местоположении B для изображения подповерхностного отражателя без каких-либо сведений о местоположении источника. .[8] Взаимная корреляция трасс A и B в частотной области упрощается как:

Уравнение 4

Ф (A, B) = - (Wiω) ^ 2 Re ^ iω (λArλrB) + o.t.

Где: Wi (ω) = вейвлет источника частотной области (i-й вейвлет)

Взаимная корреляция прямой волны в точке A с призрачным отражением в точке B удаляет неизвестный источник, где:

Уравнение 5

Ф (A, B) ≈Re ^ iω (λArλrB)

Эта форма эквивалентна конфигурации виртуального источника в точке A, отображающей гипотетические отражения в точке B. Миграция этих положений корреляции удаляет фазовый член и дает окончательное изображение миграции в позиции x, где:

m (x) = Σø (A, B, λAx + λxB) Где: ø (A, B, t) = временная корреляция между точками A и B с временем задержки t

Эта модель была применена для моделирования геометрии геологической среды в Западном Техасе с использованием смоделированных моделей, включая традиционный заглубленный источник и синтетический (виртуальный) источник вращающегося бурового долота, для получения аналогичных результатов.[8][12] Аналогичная модель продемонстрировала реконструкцию смоделированной геологической среды. геометрия.[4] В этом случае восстановленный отклик геологической среды правильно смоделировал относительное положение основных и кратных цветов. Дополнительные уравнения могут быть получены для восстановления геометрии сигнала в самых разных случаях.

Приложения

Сейсмическая интерферометрия в настоящее время используется в основном в исследовательских и академических учреждениях. В одном примере пассивное прослушивание и кросс-корреляция длинных следов шума использовались для аппроксимации импульсной характеристики для анализа скоростей на мелководье в Южной Калифорнии. Сейсмическая интерферометрия дала результат, сопоставимый с результатами, полученными при использовании сложных методов инверсии. Сейсмическая интерферометрия чаще всего используется для исследования приповерхностных слоев и часто используется только для восстановления поверхностных и прямых волн. Таким образом, сейсмическая интерферометрия обычно используется для оценки волн грунта, чтобы помочь в их удалении.[1] Сейсмическая интерферометрия упрощает оценку скорости и затухания поперечных волн в стоячем здании.[13] Сейсмическая интерферометрия была применена для изображения сейсмического рассеяния. [14] и скоростная структура [15] вулканов.

Сейсмическое отображение, записанное геофонами

Разведка и добыча

Все чаще сейсмическая интерферометрия находит свое место в исследование и производство.[16] SI может отображать погружающиеся отложения, прилегающие к соляные купола.[17] Сложные солевые геометрии плохо разрешаются при использовании традиционных сейсмическое отражение техники. Альтернативный метод требует использования скважинных источников и приемников, прилегающих к подземным солевым объектам. Часто бывает сложно создать идеальный сейсмический сигнал в скважине.[16][17] Сейсмическая интерферометрия может фактически переместить источник в скважину, чтобы лучше осветить и уловить круто падающие отложения на краю соляного купола. В этом случае результат SI был очень похож на результат, полученный с использованием реального скважинного источника. Сейсмическая интерферометрия может определить местоположение неизвестного источника и часто используется в гидроразрыв приложения для отображения протяженности индуцированных трещин.[8] Возможно, что интерферометрические методы могут быть применены для таймлапс-сейсмического мониторинга тонких изменений свойств коллектора в геологической среде.[1]

Ограничения

Применение сейсмической интерферометрии в настоящее время ограничено рядом факторов. Реальные медиа и шум представляют собой ограничения для текущих теоретических разработок. Например, чтобы интерферометрия работала источники шума должны быть некоррелированными и полностью окружать интересующую область. Кроме того, затухание и геометрическое распространение в значительной степени игнорируются и должны быть включены в более надежные модели.[1] Другие проблемы присущи сейсмической интерферометрии. Например, член источника выпадает только в случае взаимной корреляции прямой волны в точке A с призрачным отражением в точке B. Корреляция других форм волны может привести к кратным интерферограмма. Анализ и фильтрация скорости могут уменьшить, но не исключить наличие кратных значений в данном наборе данных.[8]

Несмотря на то, что в сейсмической интерферометрии было много достижений, проблемы все еще остаются. Одна из самых больших оставшихся проблем - это расширение теории для учета реальных сред и распределения шума в недрах. Природные источники обычно не соответствуют математическим обобщениям и могут фактически отображать некоторую степень корреляции.[1] Прежде чем применение сейсмической интерферометрии станет более распространенным, необходимо решить дополнительные проблемы.

Примечания

  1. ^ а б c d е ж грамм час я j k Curtis et al. 2006 г.
  2. ^ Аки, Кейити (1957). «Пространственно-временные спектры стационарных стохастических волн с особым упором на микротреморы». Вестник Института исследования землетрясений. 35: 415–457. HDL:2261/11892.
  3. ^ Клаербут, Джон Ф. (апрель 1968 г.). «Синтез слоистой среды из ITS Acoustic Transmission Response». Геофизика. 33 (2): 264–269. Bibcode:1968Геоп ... 33..264C. Дои:10.1190/1.1439927.
  4. ^ а б c d Драганов, Вапенаар и Торбек, 2006 г.
  5. ^ Уивер и Лобкис 2001
  6. ^ Вапенаар 2004
  7. ^ Кампильо и Пол 2003
  8. ^ а б c d е ж грамм час Schuster et al. 2004 г.
  9. ^ Бакулин и Калверт 2004
  10. ^ а б Вапенаар и Фоккема 2006
  11. ^ Анимация
  12. ^ Ю, Followill & Schuster 2003
  13. ^ Snieder & Safak 2006
  14. ^ Chaput et al., 2012
  15. ^ Brenguier et al. 2007 г.
  16. ^ а б Хорнби и Ю 2007
  17. ^ а б Лу и др. 2006 г.

Рекомендации