Удушенный граф - Strangulated graph

Удушенный граф, сформированный с помощью кликовые суммы склеить максимальный планарный граф (желтый) и два хордовые графы (красный и синий). Красный хордовый граф, в свою очередь, может быть разложен на клик-суммы четырех максимальных планарных графов (два ребра и два треугольника).

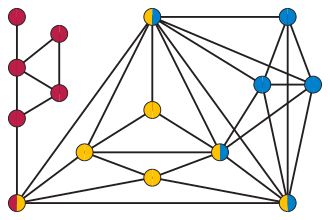
В теоретическая математика, а задушенный граф - это граф, в котором удаление ребер любых индуцированный цикл длиной больше трех Отключить оставшийся граф. То есть это графики, в которых каждый периферический цикл это треугольник.

Примеры

В максимальный планарный граф, или вообще в каждом многогранный граф, периферийные циклы - это в точности грани плоского вложения графа, поэтому многогранный граф удушен тогда и только тогда, когда все грани являются треугольниками, или, что то же самое, он максимально плоский. Каждый хордовый граф задушен, потому что единственные индуцированные циклы в хордовых графах - это треугольники, поэтому циклов для удаления больше нет.

Характеристика

А кликовая сумма двух графов образуется путем отождествления двух одинаковых по размеру клики в каждом графе, а затем, возможно, удалив некоторые ребра клики. Для версии клик-сумм, относящейся к сжатым графам, шаг удаления ребер опускается. Кликовая сумма этого типа между двумя сжатыми графами приводит к другому сжатому графу, так как каждый длинный индуцированный цикл в сумме должен быть ограничен одной или другой стороной (в противном случае у нее была бы хорда между вершинами, в которых она пересекалась с одной. сторона суммы к другой), и отключенные части этой стороны, образованные удалением цикла, должны оставаться разъединенными в клик-сумме. Таким образом, каждый хордовый граф может быть разложен на клик-сумму полные графики, и каждый максимальный планарный граф может быть разложен в клик-сумму 4-вершинно-связанный максимальные планарные графы.

В качестве Сеймур и Уивер (1984) показывают, что это единственные возможные строительные блоки сжатых графов: сжатые графы - это именно те графы, которые могут быть сформированы как клик-суммы полных графов и максимальных плоских графов.

Смотрите также

• Линейный идеальный график, граф, в котором каждый нечетный цикл представляет собой треугольник

Рекомендации

• Сеймур, П.Д.; Уивер, Р. В. (1984), "Обобщение хордовых графов", Журнал теории графов, 8 (2): 241–251, Дои:10.1002 / jgt.3190080206, МИСТЕР  0742878.