Проблема упаковки полосы - Strip packing problem

В проблема упаковки полосы представляет собой двумерную геометрическую задачу минимизации. Учитывая набор выровненных по оси прямоугольников и полосу ограниченной ширины и бесконечной высоты, определите упаковку прямоугольников в полосу без перекрытия, минимизируя ее высоту. Эта проблема связана с разрезанием и упаковкой и классифицируется как Проблема открытого измерения согласно Wäscher et al.^[1]

Эта проблема возникает в области планирования, где моделируются задания, требующие непрерывной части памяти в течение заданного периода времени. Другим примером является область промышленного производства, где прямоугольные куски необходимо вырезать из листа материала (например, ткани или бумаги), который имеет фиксированную ширину, но бесконечную длину, и нужно минимизировать потери материала.

Впервые эта проблема была изучена в 1980 году.^[2] Это сильно NP-сложный алгоритм, и не существует алгоритма полиномиальной аппроксимации времени с отношением меньше, чем ${ displaystyle 3/2}$ пока не ${ displaystyle P = NP}$. Однако лучший коэффициент приближения, достигнутый на данный момент (с помощью алгоритма полиномиального времени Харрена и др.^[3]) является ${ Displaystyle (5/3 + varepsilon)}$, ставя открытый вопрос, существует ли алгоритм с коэффициентом аппроксимации ${ displaystyle 3/2}$.

Определение

Экземпляр ${ Displaystyle I = ({ mathcal {I}}, W)}$ из проблема упаковки полосы состоит из полосы шириной ${ displaystyle W = 1}$ и бесконечной высоты, а также множество ${ displaystyle { mathcal {I}}}$ прямоугольных изделий. Каждый предмет ${ displaystyle i in { mathcal {I}}}$ имеет ширину ${ displaystyle w_ {i} in (0,1] cap mathbb {Q}}$ и высота ${ displaystyle h_ {i} in (0,1] cap mathbb {Q}}$.Пакет предметов - это отображение, которое отображает каждый нижний левый угол предмета. ${ displaystyle i in { mathcal {I}}}$ на позицию ${ displaystyle (x_ {i}, y_ {i}) in ([0,1-w_ {i}] cap mathbb {Q}) times mathbb {Q} _ { geq 0}}$ внутри полосы. Внутренняя точка размещенного предмета ${ displaystyle i in { mathcal {I}}}$ точка из множества ${ displaystyle mathrm {inn} (i) = {(x, y) in mathbb {Q} times mathbb {Q} | x_ {i}$.Два (размещенных) элемента перекрываются, если они имеют общую внутреннюю точку. Высота упаковки определяется как ${ displaystyle max {y_ {i} + h_ {i} | i in { mathcal {I}} }}$. Цель состоит в том, чтобы найти упаковку предметов внутри полосы без перекрытия при минимальной высоте упаковки.

Это определение используется для всех алгоритмов с полиномиальным временем. За псевдополиномиальное время и FPT -алгоритмов, определение немного изменено для упрощения обозначений. В этом случае все появляющиеся размеры являются целыми. В частности, ширина полосы задается произвольным целым числом больше 1. Обратите внимание, что эти два определения эквивалентны.

Варианты

Изучено несколько вариантов задачи упаковки стрипов. Эти варианты касаются геометрии объектов, размера проблемы, разрешено ли вращение предметов и структуры упаковки.^[4]

Геометрия предметов: В стандартном варианте этой задачи набор заданных элементов состоит из прямоугольников, в часто рассматриваемом подслучае все элементы должны быть квадратами. Этот вариант уже рассматривался в первой статье о стрип-упаковке.^[2]Кроме того, были изучены варианты, в которых формы имеют круглую или даже неправильную форму. В последнем случае мы говорим о упаковка нестандартных полос.

Измерение:Если не упомянуто иное, проблема упаковки полос является двумерной проблемой. Однако он также был изучен в трех или даже более измерениях. В этом случае объекты гипер прямоугольники, причем полоса является разомкнутой в одном измерении и ограниченной в остаточных.

Вращение: В классической задаче ленточной упаковки не разрешается вращать предметы. Однако изучены варианты, в которых допускается поворот на 90 градусов или даже на произвольный угол.

Состав упаковки:В общей задаче упаковки полосок структура упаковки не имеет значения. Однако есть приложения, в которых есть явные требования к структуре упаковки. Одно из этих требований - уметь разрезать элементы полосы горизонтальными или вертикальными надрезами от края до края. Упаковки, допускающие такую ​​резку, называются гильотинная упаковка.

Твердость

Проблема упаковки полосы содержит проблема с упаковкой бункера как частный случай, когда все элементы имеют одинаковую высоту 1. По этой причине это сильно NP-сложно и не может быть полиномиального времени алгоритм аппроксимации, имеющая отношение аппроксимации меньше, чем ${ displaystyle 3/2}$ пока не ${ displaystyle P = NP}$. Кроме того, если ${ displaystyle P = NP}$, не может быть псевдополиномиальное время алгоритм, который имеет коэффициент аппроксимации меньше, чем ${ displaystyle 5/4}$,^[5] что может быть доказано редукцией от сильно NP-полный Проблема с 3 разделами Обратите внимание, что обе нижние границы ${ displaystyle 3/2}$ и ${ displaystyle 5/4}$ также справедливо для случая, когда разрешен поворот предметов на 90 градусов. Кроме того, это было доказано Ashok et al.^[6] эта упаковка полосы W [1] -жесткий при параметрировании высотой оптимальной упаковки.

Свойства оптимальных решений

Есть две тривиальные нижние оценки оптимальных решений. Первый - это высота самого большого предмета. Определять ${ displaystyle h _ { max} (I): = max {h (i) | i in { mathcal {I}} }}$. Тогда считается, что

${ displaystyle OPT (I) geq h _ { max} (I)}$.

Еще одна нижняя граница определяется общей площадью предметов. Определять ${ Displaystyle mathrm {ОБЛАСТЬ} ({ mathcal {I}}): = сумма _ {я in { mathcal {I}}} ч (я) ш (я)}$ тогда он считает, что

${ displaystyle OPT (I) geq mathrm {AREA} ({ mathcal {I}}) / W}$.

Следующие две нижние границы учитывают тот факт, что некоторые элементы не могут быть размещены рядом друг с другом в полосе и могут быть вычислены в ${ Displaystyle { mathcal {O}} (п журнал (п))}$.^[7]Для первой нижней границы предположим, что элементы отсортированы по невозрастающей высоте. Определять ${ Displaystyle к: = макс {я: сумма _ {j = 1} ^ {k} вес (j) Leq W }}$. Для каждого ${ displaystyle l> k}$ определять ${ Displaystyle я (л) Leq к}$ первый индекс такой, что ${ Displaystyle вес (л) + сумма _ {j = 1} ^ {я (l)} вес (j)> W}$. Тогда считается, что

${ Displaystyle ОПТ (I) GEQ макс {ч (л) + ч (я (л)) | л> к клин ш (л) + сумма _ {j = 1} ^ {я (л) } w (j)> W }}$.^[7]

Для второй нижней границы разделите набор предметов на три набора. Позволять ${ Displaystyle альфа в [1, W / 2] cap mathbb {N}}$ и определить ${ displaystyle { mathcal {I}} _ {1} ( alpha): = {i in { mathcal {I}} | w (i)> W- alpha }}$, ${ displaystyle { mathcal {I}} _ {2} ( alpha): = {i in { mathcal {I}} | W- alpha geq w (i)> W / 2 }}$, и ${ displaystyle { mathcal {I}} _ {3} ( alpha): = {i in { mathcal {I}} | W / 2 geq w (i)> alpha }}$. Тогда считается, что

${ displaystyle OPT (I) geq max _ { alpha in [1, W / 2] cap mathbb {N}} { Bigg {} sum _ {i in { mathcal {I }} _ {1} ( alpha) cup { mathcal {I}} _ {2} ( alpha)} h (i) + left ({ frac { sum _ {i in { mathcal {I}} _ {3} ( alpha) h (i) w (i) - sum _ {i in { mathcal {I}} _ {2} ( alpha)} (Ww (i)) h (i)}} {W}} right) _ {+} { Bigg }}}$,^[7] куда ${ Displaystyle (х) _ {+}: = макс {х, 0 }}$ для каждого ${ Displaystyle х in mathbb {R}}$.

С другой стороны, Штейнберг^[8] показал, что высота оптимального решения может быть ограничена сверху величиной

${ displaystyle OPT (I) leq 2 max {h _ { max} (I), mathrm {AREA} ({ mathcal {I}}) / W }.}$

Точнее он показал, что с учетом ${ displaystyle W geq w _ { max} ({ mathcal {I}})}$ и ${ displaystyle H geq h _ { max} (I)}$ затем предметы ${ displaystyle { mathcal {I}}}$ можно разместить внутри коробки шириной ${ displaystyle W}$ и высота ${ displaystyle H}$ если

${ displaystyle WH geq 2 mathrm {AREA} ({ mathcal {I}}) + (2w _ { max} ({ mathcal {I}}) - W) _ {+} (2h _ { max} (I) -H) _ {+}}$, куда ${ Displaystyle (х) _ {+}: = макс {х, 0 }}$.

Алгоритмы полиномиальной аппроксимации времени

Поскольку эта проблема NP-сложна, аппроксимационные алгоритмы были изучены для этой проблемы. Большинство из эвристические подходы иметь отношение приближения между ${ displaystyle 3}$ и ${ displaystyle 2}$. Нахождение алгоритма с соотношением ниже ${ displaystyle 2}$ кажется трудным, и сложность соответствующих алгоритмов возрастает в зависимости от времени их работы и их описаний. Наименьший коэффициент приближения, достигнутый на данный момент, составляет ${ Displaystyle (5/3 + varepsilon)}$.

Обзор полиномиальных приближений времени

Год	Имя	Гарантия приближения	Источник
1980	Снизу вверх по левому краю (BL)	${ displaystyle 3OPT (I)}$	Бейкер и др.[2]
1980	Next-Fit с уменьшающейся высотой (NFDH)	${ Displaystyle 2OPT (I) + час _ { max} (I) leq 3OPT (I)}$	Коффман и др.[9]
	Первая посадка на убывающую высоту (FFDH)	${ displaystyle 1.7OPT (I) + h _ { max} (I) leq 2.7OPT (I)}$
	Раздельная посадка (SF)	${ displaystyle 1.5OPT (I) + 2h _ { max} (I)}$
1980		${ Displaystyle 2OPT (I) + h _ { max} (I) / 2 leq 2.5OPT (I)}$	Slaetor[10]
1981	Алгоритм разделения (SP)	${ displaystyle 3OPT (I)}$	Голаны[11]
	Смешанный алгоритм	${ displaystyle (4/3) OPT (I) +7 { frac {1} {18}} h _ { max} (I)}$
1981	Вверх-Вниз (UD)	${ displaystyle (5/4) OPT (I) +6 { frac {7} {8}} h _ { max} (I)}$	Бейкер и др.[12]
1994	Обратная посадка	${ displaystyle 2OPT (I)}$	Ширмейер[13]
1997		${ displaystyle 2OPT (I)}$	Steinberg[8]
2000		${ Displaystyle (1+ varepsilon) OPT (I) + { mathcal {O}} (1 / varepsilon ^ {2}) h _ { max} (I)}$	Кеньон, Ремила[14]
2009		${ displaystyle 1.9396OPT (I)}$	Харрен, ван Сти[15]
2009		${ displaystyle (1+ varepsilon) OPT (I) + h _ { max} (I)}$	Янсен, Солис-Оба[16]
2011		${ Displaystyle (1+ varepsilon) OPT (I) + { mathcal {O}} ( log (1 / varepsilon) / varepsilon) h _ { max} (I)}$	Bougeret et al.[17]
2012		${ Displaystyle (1+ varepsilon) OPT (I) + { mathcal {O}} ( log (1 / varepsilon) / varepsilon) h _ { max} (I)}$	Свириденко[18]
2014		${ Displaystyle (5/3 + varepsilon) OPT (I)}$	Harren et al.[3]

Снизу вверх по левому краю (BL)

Пример решений, генерируемых алгоритмом Bottom-Up Left-Justified.

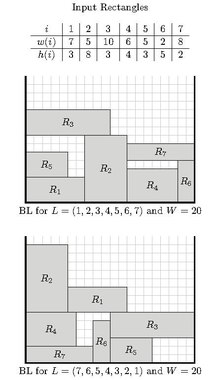
Этот алгоритм был впервые описан Baker et al.^[2] Это работает следующим образом:

Позволять ${ displaystyle L}$ быть последовательностью прямоугольных элементов. Алгоритм выполняет итерацию последовательности в заданном порядке. По каждому рассматриваемому пункту ${ displaystyle r in L}$, он ищет самое нижнее положение, чтобы разместить его, а затем сдвигает его как можно дальше влево. Следовательно, он помещает ${ displaystyle r}$ в самой нижней левой самой возможной координате ${ Displaystyle (х, у)}$ в полосе.

Этот алгоритм имеет следующие свойства:

• Коэффициент аппроксимации этого алгоритма не может быть ограничен константой. Точнее показали, что для каждого ${ displaystyle M> 0}$ существует список ${ displaystyle L}$ прямоугольных элементов, упорядоченных путем увеличения ширины так, чтобы ${ Displaystyle BL (L) / OPT (L)> M}$, куда ${ displaystyle BL (L)}$ - высота упаковки, созданной алгоритмом BL, и ${ displaystyle OPT (L)}$ - высота оптимального решения для ${ displaystyle L}$.^[2]
• Если элементы упорядочены по уменьшению ширины, то ${ Displaystyle BL (L) / OPT (L) leq 3}$.^[2]
• Если все элементы квадратные и упорядочены по убыванию ширины, тогда ${ Displaystyle BL (L) / OPT (L) leq 2}$.^[2]
• Для любого ${ displaystyle delta> 0}$, существует список ${ displaystyle L}$ прямоугольников, упорядоченных по убыванию ширины, так что ${ Displaystyle BL (L) / OPT (L)> 3- delta}$.^[2]
• Для любого ${ displaystyle delta> 0}$, существует список ${ displaystyle L}$ квадратов, упорядоченных по убыванию ширины, так что ${ Displaystyle BL (L) / OPT (L)> 2- delta}$.^[2]
• Для каждого ${ Displaystyle varepsilon в (0,1]}$, существует экземпляр, содержащий только квадраты, где каждый порядок квадратов ${ displaystyle L}$ имеет соотношение ${ displaystyle BL (L) / OPT (L)> { frac {12} {11+ varepsilon}}}$, т.е. существуют случаи, когда BL нет найти оптимальный даже при повторении всех возможных порядков элементов.^[2]

Следующая посадка с уменьшающейся высотой (NFDH)

Пример для NFDH и FFDH, примененных к одному и тому же экземпляру

Этот алгоритм был впервые описан Coffman et al.^[9] в 1980 году и работает следующим образом:

Позволять ${ displaystyle { mathcal {I}}}$ - данный набор прямоугольных элементов. Сначала алгоритм сортирует элементы в порядке невозрастания высоты, а затем начиная с позиции ${ displaystyle (0,0)}$, алгоритм размещает элементы рядом друг с другом в полосе до тех пор, пока следующий элемент не будет перекрывать правую границу полосы. На этом этапе алгоритм определяет новый уровень в верхней части самого высокого элемента на текущем уровне и помещает предметы рядом друг с другом на этом новом уровне.

Этот алгоритм имеет следующие свойства:

• Время работы может быть ограничено ${ Displaystyle { mathcal {O}} (| { mathcal {I}} | log (| { mathcal {I}} |))}$ и если товары уже отсортированы даже по ${ Displaystyle { mathcal {O}} (| { mathcal {I}} |)}$.
• Для каждого набора предметов ${ displaystyle { mathcal {I}}}$, производит упаковку высотой ${ Displaystyle NFDH ({ mathcal {I}}) leq 2OPT ({ mathcal {I}}) + h _ { max} leq 3OPT ({ mathcal {I}})}$, куда ${ displaystyle h _ { max}}$ это самая большая высота предмета в ${ displaystyle { mathcal {I}}}$.^[9]
• Для каждого ${ displaystyle varepsilon> 0}$ существует набор прямоугольников ${ displaystyle { mathcal {I}}}$ такой, что ${ displaystyle NFDH ({ mathcal {I}} |)> (2- varepsilon) OPT ({ mathcal {I}}).}$^[9]
• Созданная насадка представляет собой гильотинную насадку. Это означает, что элементы могут быть получены с помощью последовательности горизонтальных или вертикальных разрезов от края до края.

Первая посадка на убывающую высоту (FFDH)

Этот алгоритм, впервые описанный Coffman et al.^[9] в 1980 году работает аналогично алгоритму NFDH. Однако при размещении следующего элемента алгоритм сканирует уровни снизу вверх и помещает элемент на первый уровень, на котором он поместится. Новый уровень открывается только в том случае, если предмет не помещается ни на одном из предыдущих.

Этот алгоритм имеет следующие свойства:

• Время работы может быть ограничено ${ Displaystyle { mathcal {O}} (| { mathcal {I}} | ^ {2})}$, так как есть не более ${ displaystyle | { mathcal {I}} |}$ уровни.
• Для каждого набора предметов ${ displaystyle { mathcal {I}}}$ производит упаковку высотой ${ Displaystyle FFDH ({ mathcal {I}}) leq 1.7OPT ({ mathcal {I}}) + h _ { max} leq 2.7OPT ({ mathcal {I}})}$, куда ${ displaystyle h _ { max}}$ это самая большая высота предмета в ${ displaystyle { mathcal {I}}}$.^[9]
• Позволять ${ displaystyle m geq 2}$. Для любого набора предметов ${ displaystyle { mathcal {I}}}$ и полоса шириной ${ displaystyle W}$ такой, что ${ Displaystyle ш (я) leq Вт / м}$ для каждого ${ displaystyle i in { mathcal {I}}}$, считается, что ${ Displaystyle FFDH ({ mathcal {I}}) leq left (1 + 1 / m right) OPT ({ mathcal {I}}) + h _ { max}}$. Кроме того, для каждого ${ displaystyle varepsilon> 0}$, существует такой набор предметов ${ displaystyle { mathcal {I}}}$ с ${ Displaystyle FFDH ({ mathcal {I}})> left (1 + 1 / m- varepsilon right) OPT ({ mathcal {I}})}$.^[9]
• Если все предметы в ${ displaystyle { mathcal {I}}}$ являются квадратами, то ${ Displaystyle FFDH ({ mathcal {I}}) leq (3/2) OPT ({ mathcal {I}}) + ч _ { max}}$. Кроме того, для каждого ${ displaystyle varepsilon> 0}$, существует набор квадратов ${ displaystyle { mathcal {I}}}$ такой, что ${ Displaystyle FFDH ({ mathcal {I}})> left (3/2- varepsilon right) OPT ({ mathcal {I}})}$.^[9]
• Созданная насадка представляет собой гильотинную насадку. Это означает, что элементы могут быть получены путем последовательной резки по горизонтали или вертикали от края до края.

Алгоритм раздельной подгонки (SF)

Этот алгоритм был впервые описан Coffman et al.^[9] Для заданного набора предметов ${ displaystyle { mathcal {I}}}$ и полоса шириной ${ displaystyle W}$, это работает следующим образом:

1. Решительный ${ displaystyle m in mathbb {N}}$, наибольшее целое число такое, что заданные прямоугольники имеют ширину ${ Displaystyle Вт / м}$ или менее.
2. Разделять ${ displaystyle { mathcal {I}}}$ на два набора ${ displaystyle { mathcal {I}} _ {широкий}}$ и ${ displaystyle { mathcal {I}} _ {узкий}}$, так что ${ displaystyle { mathcal {I}} _ {широкий}}$ содержит все предметы ${ displaystyle i in { mathcal {I}}}$ с шириной ${ Displaystyle ш (я)> Вт / (м + 1)}$ пока ${ displaystyle { mathcal {I}} _ {узкий}}$ содержит все предметы с ${ Displaystyle ш (я) Leq Вт / (м + 1)}$.
3. Заказ ${ displaystyle { mathcal {I}} _ {широкий}}$ и ${ displaystyle { mathcal {I}} _ {узкий}}$ по невозрастающей высоте.
4. Упакуйте предметы в ${ displaystyle { mathcal {I}} _ {широкий}}$ с алгоритмом FFDH.
5. Измените порядок уровней / полок, построенных FFDH, таким образом, чтобы все полки общей шириной больше ${ Displaystyle W (м + 1) / (м + 2)}$ находятся ниже более узких.
6. Это оставляет прямоугольную область ${ displaystyle R}$ из с ${ Displaystyle W / (м + 2)}$, рядом с более узкими уровнями / полками, на которых нет предметов.
7. Используйте алгоритм FFDH для упаковки предметов в ${ displaystyle { mathcal {I}} _ {узкий}}$ используя площадь ${ displaystyle R}$ также.

Этот алгоритм имеет следующие свойства:

• Для каждого набора предметов ${ displaystyle { mathcal {I}}}$ и соответствующие ${ displaystyle m}$, считается, что ${ Displaystyle SF ({ mathcal {I}}) leq (m + 2) / (m + 1) OPT ({ mathcal {I}}) + 2h _ { max}}$.^[9] Обратите внимание, что для ${ displaystyle m = 1}$, считается, что ${ Displaystyle SF ({ mathcal {I}}) leq (3/2) OPT ({ mathcal {I}}) + 2h _ { max}}$
• Для каждого ${ displaystyle varepsilon> 0}$, есть набор предметов ${ displaystyle { mathcal {I}}}$ такой, что ${ Displaystyle SF ({ mathcal {I}})> left ((m + 2) / (m + 1) - varepsilon right) OPT ({ mathcal {I}})}$.^[9]

Алгоритм Слейтора

Для заданного набора предметов ${ displaystyle { mathcal {I}}}$ и полоса шириной ${ displaystyle W}$, это работает следующим образом:

1. Найдите все предметы шириной больше, чем ${ Displaystyle W / 2}$ и сложите их внизу полосы (в произвольном порядке). Назовите общую высоту этих предметов ${ displaystyle h_ {0}}$. Все остальные предметы будут размещены выше ${ displaystyle h_ {0}}$.
2. Отсортируйте все оставшиеся элементы в порядке невозрастания по высоте. Предметы будут размещены в этом порядке.
3. Рассмотрим горизонтальную линию на ${ displaystyle h_ {0}}$ как полка. Алгоритм размещает элементы на этой полке в порядке невозрастания по высоте, пока не останется ни одного элемента или не поместится следующий.
4. Проведите вертикальную линию на ${ Displaystyle W / 2}$, который разрезает полосу на две равные половины.
5. Позволять ${ displaystyle h_ {l}}$ быть наивысшей точкой, покрываемой любым предметом в левой половине, и ${ displaystyle h_ {r}}$ соответствующая точка в правой половине. Нарисуйте два отрезка горизонтальной линии длины ${ Displaystyle W / 2}$ в ${ displaystyle h_ {l}}$ и ${ displaystyle h_ {r}}$ через левую и правую половину полосы. Эти две строки создают новые полки, на которые алгоритм будет размещать предметы, как на шаге 3. Выберите половину, у которой есть нижняя полка, и поместите предметы на эту полку, пока не поместятся другие предметы. Повторяйте этот шаг, пока не останется ни одного элемента.

Этот алгоритм имеет следующие свойства:

• Время работы может быть ограничено ${ Displaystyle { mathcal {O}} (| { mathcal {I}} | log (| { mathcal {I}} |))}$ и если товары уже отсортированы даже по ${ Displaystyle { mathcal {O}} (| { mathcal {I}} |)}$.
• Для каждого набора предметов ${ displaystyle { mathcal {I}}}$ производит упаковку высотой ${ Displaystyle А ({ mathcal {I}}) leq 2OPT ({ mathcal {I}}) + h _ { max} / 2 leq 2.5OPT ({ mathcal {I}})}$, куда ${ displaystyle h _ { max}}$ это самая большая высота предмета в ${ displaystyle { mathcal {I}}}$.^[10]

Алгоритм разделения (SP)

Этот алгоритм является расширением подхода Sleator и впервые был описан Голаном.^[11] Он размещает элементы в порядке невозрастания ширины. Интуитивно понятная идея состоит в том, чтобы разделить полосу на подполосы при размещении некоторых элементов. По возможности алгоритм помещает текущий элемент ${ displaystyle i}$ рядом с уже размещенным элементом ${ displaystyle j}$. В этом случае он разделяет соответствующую подполоску на две части: одна содержит первый элемент. ${ displaystyle j}$ а другой, содержащий текущий элемент ${ displaystyle i}$.Если это невозможно, он помещает ${ displaystyle i}$ поверх уже размещенного элемента и не разделяет подполоску.

Этот алгоритм создает набор S суб-полос. Для каждой подполосы s ∈ S мы знаем его нижний левый угол s.xposition и s.yposition, его ширина s.width, горизонтальные линии, параллельные верхней и нижней границе элемента, помещенного последним внутри этой подполосы ужин и помедленнее, а также его ширину s.itemWidth.

функция Алгоритм разделения (SP) является    Вход: Предметы я, ширина полосы W    выход: Упаковка предметов    Сортировать I в порядке невозрастания ширины; Определите пустой список S подполос; Определите новую подполосу s с s.xposition = 0, s.yposition = 0, s.width = W, s.lower = 0, s.upper = 0, s.itemWidth = W; Добавить s к S; пока Я не пустой делать        я: = I.pop (); Удаляет самый широкий элемент из I Определите новый список S_2, содержащий все подстроки с s.width - s.itemWidth ≥ i.width; S_2 содержит все подполосы, где i помещается рядом с уже размещенным элементом        если S_2 пуст тогда            В этом случае поместите предмет поверх другого.            Найдите подполоску s в S с наименьшим s.upper; т.е. наименее заполненная подполоса            Поместите i в позицию (s.xposition, s.upper); Обновление s: s.lower: = s.upper; s.upper: = s.upper + i.height; s.itemWidth: = i.width; еще             В этом случае поместите элемент рядом с другим на том же уровне и разделите соответствующую подполоску в этом месте.            Найдите s ∈ S_2 с наименьшим значением s.low; Поместите i в позицию (s.xposition + s.itemWidth, s.lower); Удалите s из S; Определите две новые поддиапазоны s1 и s2 с помощью s1.xposition = s.xposition, s1.yposition = s.upper, s1.width = s.itemWidth, s1.lower = s.upper, s1.upper = s.upper, s1.itemWidth = s.itemWidth; s2.xposition = s.xposition + s.itemWidth, s2.yposition = s.lower, s2.width = s.width - s.itemWidth, s2.lower = s.lower, s2.upper = i.height, s2. itemWidth = i.width; S.add (s1, s2); возвращаться конечная функция

Этот алгоритм имеет следующие свойства:

• Время работы может быть ограничено ${ Displaystyle { mathcal {O}} (| { mathcal {I}} | ^ {2})}$ так как количество подстилок ограничено ${ displaystyle | { mathcal {I}} |}$.
• Для любого набора предметов ${ displaystyle { mathcal {I}}}$ он считает, что ${ Displaystyle SP ({ mathcal {I}}) leq 2OPT ({ mathcal {I}}) + h _ { max} leq 3OPT ({ mathcal {I}})}$.^[11]
• Для любого ${ displaystyle varepsilon> 0}$, существует набор предметов ${ displaystyle { mathcal {I}}}$ такой, что ${ Displaystyle SP ({ mathcal {I}})> (3- varepsilon) OPT ({ mathcal {I}})}$.^[11]
• Для любого ${ displaystyle varepsilon> 0}$ и ${ displaystyle C> 0}$, существует набор предметов ${ displaystyle { mathcal {I}}}$ такой, что ${ Displaystyle SP ({ mathcal {I}})> (2- varepsilon) OPT ({ mathcal {I}}) + C}$.^[11]

Обратная посадка (RF)

Этот алгоритм был впервые описан Ширмейером.^[13] Описание этого алгоритма требует дополнительных обозначений. Для размещенного товара ${ displaystyle i in { mathcal {I}}}$, его левый нижний угол обозначается ${ Displaystyle (а_ {я}, с_ {я})}$ и его правый верхний угол на ${ displaystyle (b_ {i}, d_ {i})}$.

Учитывая набор предметов ${ displaystyle { mathcal {I}}}$ и полоса шириной ${ displaystyle W}$, это работает следующим образом:

1. Сложите все прямоугольники шириной больше, чем ${ Displaystyle W / 2}$ друг на друга (в произвольном порядке) внизу полосы. Обозначим через ${ displaystyle H_ {0}}$ высота этой стопки. Все остальные предметы будут упакованы выше ${ displaystyle H_ {0}}$.
2. Отсортируйте оставшиеся элементы в порядке невозрастания высоты и рассмотрите элементы в этом порядке на следующих шагах. Позволять ${ displaystyle h _ { max}}$ быть высотой самого высокого из этих оставшихся предметов.
3. Поместите предметы по одному по левому краю на полку, обозначенную ${ displaystyle H_ {0}}$ до тех пор, пока на эту полку не поместится другой предмет или не останется ничего. Назовите эту полку Первый уровень.
4. Позволять ${ displaystyle h_ {1}}$ быть высотой самого высокого распакованного предмета. Определите новую полку в ${ displaystyle H_ {0} + h _ { max} + h_ {1}}$. Алгоритм заполняет эту полку справа налево, выравнивая элементы по правому краю, так что предметы касаются этой полки своим верхом. Назовите эту полку второй обратный уровень.
5. Поместите предметы на две полки в соответствии с функцией First-Fit, т. Е. Разместите предметы на первом уровне там, где они подходят, и на втором в противном случае. Продолжайте до тех пор, пока ничего не останется, или пока общая ширина предметов на второй полке не станет не менее ${ Displaystyle W / 2}$.
6. Сдвиньте второй обратный уровень вниз, пока элемент из него не коснется элемента из первого уровня. Определять ${ displaystyle H_ {1}}$ как новое вертикальное положение смещенной полки. Позволять ${ displaystyle f}$ и ${ displaystyle s}$ быть самой правильной парой трогательных предметов с ${ displaystyle f}$ размещен на первом уровне и ${ displaystyle s}$ на втором обратном уровне. Определять ${ displaystyle x_ {r}: = max (b_ {f}, b_ {s})}$.
7. Если ${ displaystyle x_ {r}$ тогда ${ displaystyle s}$ - последний прямоугольник, помещенный на втором обратном уровне. Переместите все остальные предметы с этого уровня ниже (на все одинаковое количество), пока первый не коснется предмета с первого уровня. Снова алгоритм определяет крайнюю правую пару соприкасающихся предметов. ${ displaystyle f '}$ и ${ displaystyle s '}$. Определять ${ displaystyle h_ {2}}$ как величина, на которую полка была сдвинута вниз.
   1. Если ${ displaystyle h_ {2} leq h (s)}$ тогда сдвиг ${ displaystyle s}$ влево, пока не коснется другого предмета или границы полосы. Определите третий уровень вверху ${ displaystyle s '}$.
   2. Если ${ displaystyle h_ {2}> h (s)}$ тогда сдвиг ${ displaystyle s}$ определить третий уровень в верхней части ${ displaystyle s '}$. Место ${ displaystyle s}$ с выравниванием по левому краю на этом третьем уровне, так что он касается элемента с первого уровня слева от него.
8. Продолжайте упаковывать элементы, используя эвристику First-Fit. Каждый последующий уровень (начиная с третьего уровня) определяется горизонтальной линией, проходящей через верх самого большого элемента на предыдущем уровне. Обратите внимание, что первый элемент, помещенный на следующий уровень, может касаться не границы полосы своей левой стороной, а предмет с первого уровня или предмет ${ displaystyle s}$.

Этот алгоритм имеет следующие свойства:

• Время работы может быть ограничено ${ Displaystyle { mathcal {O}} (| { mathcal {I}} | ^ {2})}$, так как есть не более ${ displaystyle | { mathcal {I}} |}$ уровни.
• Для каждого набора предметов ${ displaystyle { mathcal {I}}}$ производит упаковку высотой ${ Displaystyle RF ({ mathcal {I}}) leq 2OPT ({ mathcal {I}})}$.^[13]

Алгоритм Стейнберга (ST)

Алгоритм Стейнберга - рекурсивный. Учитывая набор прямоугольных предметов ${ displaystyle { mathcal {I}}}$ и прямоугольная целевая область шириной ${ displaystyle W}$ и высота ${ displaystyle H}$, он предлагает четыре правила сокращения, которые размещают некоторые элементы и оставляют меньшую прямоугольную область с теми же свойствами, что и раньше, в отношении остаточных элементов. Рассмотрим следующие обозначения: Дан набор элементов ${ displaystyle { mathcal {I}}}$ мы обозначим через ${ Displaystyle ч _ { макс} ({ mathcal {I}})}$ самая высокая высота предмета в ${ displaystyle { mathcal {I}}}$, ${ Displaystyle ш _ { макс} ({ mathcal {I}})}$ самая большая ширина элемента появляется в ${ displaystyle { mathcal {I}}}$ и по ${ displaystyle mathrm {AREA} ({ mathcal {I}}): = сумма _ {я in { mathcal {I}}} ш (я) ч (я)}$ общая площадь этих предметов. Стейнбергс показывает, что если

${ Displaystyle ч _ { макс} ({ mathcal {I}}) leq H}$, ${ Displaystyle ш _ { макс} ({ mathcal {I}}) leq W}$, и ${ displaystyle mathrm {AREA} ({ mathcal {I}}) leq W cdot H- (2h _ { max} ({ mathcal {I}}) - h) _ {+} (2w _ { max} ({ mathcal {I}}) - W) _ {+}}$, куда ${ Displaystyle (а) _ {+}: = макс {0, а }}$,

тогда все элементы могут быть размещены в целевой области размера ${ displaystyle W times H}$.Каждое правило уменьшения приведет к уменьшению целевой области и подмножеству элементов, которые необходимо разместить. Если указанное выше условие выполняется до запуска процедуры, то созданная подзадача также будет иметь это свойство.

Процедура 1: Может применяться, если ${ Displaystyle ш _ { макс} ({ mathcal {I}} ') geq W / 2}$.

1. Найдите все предметы ${ displaystyle i in { mathcal {I}}}$ с шириной ${ Displaystyle ш (я) geq W / 2}$ и удалите их из ${ displaystyle { mathcal {I}}}$.
2. Отсортируйте их по невозрастающей ширине и разместите по левому краю в нижней части целевой области. Позволять ${ displaystyle h_ {0}}$ быть их общей высотой.
3. Найдите все предметы ${ displaystyle i in { mathcal {I}}}$ с шириной ${ displaystyle h (i)> H-h_ {0}}$. Удалите их из ${ displaystyle { mathcal {I}}}$ и поместите их в новый набор ${ displaystyle { mathcal {I}} _ {H}}$.
4. Если ${ displaystyle { mathcal {I}} _ {H}}$ пусто, определите новую целевую область как область выше ${ displaystyle h_ {0}}$, т.е. имеет высоту ${ displaystyle H-h_ {0}}$ и ширина ${ displaystyle W}$. Решите проблему, состоящую из этого нового целевого региона и сокращенного набора элементов, с помощью одной из процедур.
5. Если ${ displaystyle { mathcal {I}} _ {H}}$ не пусто, отсортируйте его по невозрастающей высоте и поместите элементы, расположив их по одному, в правом верхнем углу целевой области. Позволять ${ displaystyle w_ {0}}$ быть общей шириной этих элементов. Определите новую целевую область с шириной ${ displaystyle W-w_ {0}}$ и высота ${ displaystyle H-h_ {0}}$ в верхнем левом углу. Решите проблему, состоящую из этого нового целевого региона и сокращенного набора элементов, с помощью одной из процедур.

Процедура 2: Может применяться, если выполняются следующие условия: ${ Displaystyle ш _ { макс} ({ mathcal {I}}) leq W / 2}$, ${ Displaystyle ч _ { макс} ({ mathcal {I}}) leq H / 2}$, и существуют два разных элемента ${ Displaystyle я, я ' in { mathcal {I}}}$ с ${ Displaystyle ш (я) geq W / 4}$, ${ Displaystyle ш (я ') geq W / 4}$, ${ Displaystyle ч (я) geq H / 4}$, ${ Displaystyle ч (я ') geq H / 4}$ и ${ Displaystyle 2 ( mathrm {ОБЛАСТЬ} ({ mathcal {I}}) - вес (я) ч (я) -w (я ') ч (я')) Leq (W- макс {ш (i), w (i ') }) H}$.

1. Находить ${ displaystyle i}$ и ${ displaystyle i '}$ и удалите их из ${ displaystyle { mathcal {I}}}$.
2. Поместите более широкий в нижний левый угол целевой области, а более узкий с выравниванием по левому краю поверх первого.
3. Определите новую целевую область справа от этих обоих элементов так, чтобы она имела ширину ${ Displaystyle W- макс {вес (я), вес (я) }}$ и высота ${ displaystyle H}$.
4. Поместите оставшиеся предметы в ${ displaystyle { mathcal {I}}}$ в новую целевую область, используя одну из процедур.

Процедура 3: Может применяться, если выполняются следующие условия: ${ Displaystyle ш _ { макс} ({ mathcal {I}}) leq W / 2}$, ${ Displaystyle ч _ { макс} ({ mathcal {I}}) leq H / 2}$, ${ displaystyle | { mathcal {I}} |> 1}$, а при сортировке элементов по уменьшению ширины существует индекс ${ displaystyle m}$ так что при определении ${ displaystyle { mathcal {I '}}}$ как первый ${ displaystyle m}$ предметы, которые он держит ${ displaystyle mathrm {AREA} ({ mathcal {I}}) - WH / 4 leq mathrm {AREA} ({ mathcal {I '}}) leq 3WH / 8}$ а также ${ Displaystyle ш (я_ {м + 1}) leq W / 4}$

1. Набор ${ displaystyle W_ {1}: = max {W / 2,2 mathrm {AREA} ({ mathcal {I '}}) / H}}$.
2. Определите две новые прямоугольные целевые области, одну в нижнем левом углу исходной с высотой ${ displaystyle H}$ и ширина ${ displaystyle W_ {1}}$ а другой слева от него с высотой ${ displaystyle H}$ и ширина ${ displaystyle W-W_ {1}}$.
3. Используйте одну из процедур, чтобы поместить предметы в ${ displaystyle { mathcal {I '}}}$ в первую новую целевую область и предметы в ${ Displaystyle { mathcal {I}} setminus { mathcal {I '}}}$ во вторую.

Обратите внимание, что процедуры с 1 по 3 имеют симметричную версию при замене местами высоты и ширины элементов и целевой области.

Процедура 4: Может применяться, если выполняются следующие условия: ${ Displaystyle ш _ { макс} ({ mathcal {I}}) leq W / 2}$, ${ Displaystyle ч _ { макс} ({ mathcal {I}}) leq H / 2}$, и существует элемент ${ displaystyle i in { mathcal {I}}}$ такой, что ${ Displaystyle ш (я) час (я) geq mathrm {ОБЛАСТЬ} ({ mathcal {I}}) - WH / 4}$.

1. Поместите предмет ${ displaystyle i}$ в нижнем левом углу целевой области и удалите его из ${ displaystyle { mathcal {I}}}$.
2. Определите новую целевую область справа от этого элемента так, чтобы она имела ширину ${ displaystyle W-w (я)}$ и высота ${ displaystyle H}$ и поместите остаточные предметы внутрь этой области, используя одну из процедур.

Этот алгоритм имеет следующие свойства:

• Время работы может быть ограничено ${ displaystyle { mathcal {O}} (| { mathcal {I}} | log (| { mathcal {I}} |) ^ {2} / log ( log (| { mathcal {I }} |)))}$.^[8]
• Для каждого набора предметов ${ displaystyle { mathcal {I}}}$ производит упаковку высотой ${ Displaystyle ST ({ mathcal {I}}) leq 2OPT ({ mathcal {I}})}$.^[8]

Псевдополиномиальные алгоритмы аппроксимации времени

Чтобы улучшить нижнюю границу ${ displaystyle 3/2}$ для алгоритмов с полиномиальным временем рассмотрены алгоритмы с псевдополиномиальным временем для задачи упаковки полос. При рассмотрении алгоритмов этого типа все размеры элементов и полосы задаются в виде интегралов. Кроме того, ширина полосы ${ displaystyle W}$ может появляться полиномиально во времени выполнения. Обратите внимание, что это больше не считается полиномиальным временем выполнения, поскольку в данном случае ширина полосы требует размера кодирования, равного ${ Displaystyle журнал (W)}$.

В разработанных псевдополиномиальных временных алгоритмах в основном используется тот же подход. Показано, что каждое оптимальное решение можно упростить и преобразовать в одно из постоянного числа структур. Затем алгоритм выполняет итерацию всех этих структур и помещает элементы внутрь с помощью линейного и динамического программирования. Лучшее соотношение, достигнутое на данный момент, - ${ Displaystyle (5/4 + varepsilon) OPT (I)}$.^[19] в то время как не может быть псевдополиномиального алгоритма времени с соотношением лучше, чем ${ displaystyle 5/4}$ пока не ${ displaystyle P = NP}$^[5]

Обзор аппроксимаций псевдополиномиального времени

Год	Коэффициент приближения	Источник	Комментарий
2010	${ Displaystyle (3/2 + varepsilon)}$	Янсен, Тёле[20]
2016	${ Displaystyle (7/5 + varepsilon)}$	Надирадзе, Визе[21]
2016	${ Displaystyle (4/3 + varepsilon)}$	Гальвес, Грандони, Ингала, Хан[22]	также для поворота на 90 градусов
2017	${ Displaystyle (4/3 + varepsilon)}$	Янсен, Рау[23]
2019	${ Displaystyle (5/4 + varepsilon)}$	Янсен, Рау[19]	также для поворота на 90 градусов и непрерывных формовочных работ

Онлайн-алгоритмы

в онлайн-вариант Ленточной упаковки товары прибывают со временем. Когда приходит предмет, он должен быть размещен непосредственно перед тем, как станет известен следующий предмет. Были рассмотрены два типа онлайн-алгоритмов. В первом варианте нельзя менять упаковку после размещения предмета. Во втором случае предметы могут быть переупакованы по прибытии другого предмета. Этот вариант называется миграционной моделью.

Качество онлайн-алгоритма измеряется (абсолютным) коэффициентом конкуренции.

${ Displaystyle mathrm {sup} _ {I} A (I) / OPT (I)}$,

куда ${ Displaystyle A (I)}$ соответствует решению, сгенерированному онлайн-алгоритмом, и ${ displaystyle OPT (I)}$ соответствует размеру оптимального решения. В дополнение к абсолютному коэффициенту конкуренции изучается асимптотический коэффициент конкуренции онлайн-алгоритмов. Например ${ displaystyle I}$ с ${ Displaystyle ч _ { макс} (я) leq 1}$ это определяется как

${ Displaystyle lim mathrm {sup} _ {OPT (I) rightarrow infty} A (I) / OPT (I)}$.

Обратите внимание, что все экземпляры можно масштабировать так, чтобы ${ Displaystyle ч _ { макс} (я) leq 1}$.

Обзор онлайн-алгоритмов без миграции

Год	Конкурентное соотношение	Асимптотический коэффициент конкуренции	Источник
1983	6.99	${ displaystyle приблизительно 1,7}$	Бейкер и Шварц[24]
1997		${ displaystyle 1.69+ varepsilon}$	Чирик и Вегингер[25]
2007	6.6623		Хуринк и Паулюс[26]
2009	6.6623		Е, Хан и Чжан[27]
2007		${ displaystyle 1.58889}$	Han et al.[28] + Сейден[29]

Структура Han et al.^[28] применимо в онлайн-настройке, если онлайн-алгоритм упаковки бункеров относится к классу Super Harmonic. Таким образом, алгоритм онлайн-упаковки Seiden Harmonic ++^[29] подразумевает алгоритм упаковки полосы в режиме онлайн с асимптотическим соотношением 1,58889.

Обзор нижних оценок онлайн-алгоритмов без миграции

Год	Конкурентное соотношение	Асимптотический коэффициент конкуренции	Источник	Комментарий
1982	${ displaystyle 2}$		Браун, Бейкер и Кацефф[30]
2006	2.25		Йоханнес[31]	также справедливо для задачи планирования параллельных задач
2007	2.43		Хуринк и Паулюс[32]	также справедливо для задачи планирования параллельных задач
2009	2.457		Керн и Паулюс [33]
2012		${ displaystyle 1.5404}$	Балог и Бекеши[34]	нижняя граница из-за основной проблемы с упаковкой бункера
2016	2.618		Ю, Мао и Сяо[35]

Рекомендации