Функция Tanc - Tanc function

В математике Функция Tanc определяется как^[1]

${ displaystyle operatorname {Tanc} (z) = { frac { tan (z)} {z}}}$

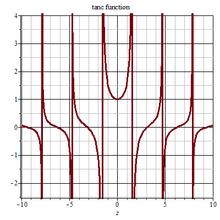
Сюжет Tanc 2D

Tanc '(z) 2D график

Интегральный 2D график Tanc

Интегральный трехмерный график Tanc

Мнимая часть в комплексной плоскости

• ${ displaystyle operatorname {Im} left ({ frac { tan (x + iy)} {x + iy}} right)}$

Реальная часть в комплексной плоскости

• ${ displaystyle operatorname {Re} left ({ frac { tan left (x + iy right)} {x + iy}} right)}$

абсолютная величина

• ${ displaystyle left | { frac { tan (x + iy)} {x + iy}} right |}$

Производная первого порядка

• ${ displaystyle { frac {1 - ( tan (z)) ^ {2}} {z}} - { frac { tan (z)} {z ^ {2}}}}$

Реальная часть производной

• ${ displaystyle - operatorname {Re} left (- { frac {1 - ( tan (x + iy)) ^ {2}} {x + iy}} + { frac { tan (x + iy) )} {(x + iy) ^ {2}}} right)}$

Мнимая часть производной

• ${ displaystyle - operatorname {Im} left (- { frac {1 - ( tan (x + iy)) ^ {2}} {x + iy}} + { frac { tan (x + iy) )} {(x + iy) ^ {2}}} right)}$

абсолютное значение производной

• ${ displaystyle left | - { frac {1 - ( tan (x + iy)) ^ {2}} {x + iy}} + { frac { tan (x + iy)} {(x + iy) ^ {2}}} right |}$

Что касается других специальных функций

• ${ displaystyle operatorname {Tanc} (z) = { frac {2 , я {{ rm {KummerM}} left (1, , 2, , 2 , iz right)}} { left (2 , z + pi right) {{ rm {KummerM}} left (1, , 2, , i left (2 , z + pi right) right)}}}}$

• ${ displaystyle operatorname {Tanc} (z) = { frac {2i operatorname {HeunB} left (2,0,0,0, { sqrt {2}} { sqrt {iz}} right) } {(2z + pi) operatorname {HeunB} left (2,0,0,0, { sqrt {2}} { sqrt {(i / 2) (2z + pi)}} right)} }}$
• ${ displaystyle operatorname {Tanc} (z) = { frac {{ rm {WhittakerM}} (0, , 1/2, , 2 , iz)} {{ rm {WhittakerM}} (0 , , 1/2, , i (2z + pi)) z}}}$

Расширение серии

${ displaystyle operatorname {Tanc} z приблизительно left (1 + { frac {1} {3}} z ^ {2} + { frac {2} {15}} z ^ {4} + { frac {17} {315}} z ^ {6} + { frac {62} {2835}} z ^ {8} + { frac {1382} {155925}} z ^ {10} + { frac { 21844} {6081075}} z ^ {12} + { frac {929569} {638512875}} z ^ {14} + O (z ^ {16}) right)}$

${ displaystyle int _ {0} ^ {z} { frac { tan (x)} {x}} , dx = left (z + { frac {1} {9}} z ^ {3} + { frac {2} {75}} z ^ {5} + { frac {17} {2205}} z ^ {7} + { frac {62} {25515}} z ^ {9} + { frac {1382} {1715175}} z ^ {11} + { frac {21844} {79053975}} z ^ {13} + { frac {929569} {9577693125}} z ^ {15} + O (z ^ {17}) right)}$

Приближение Паде

${ displaystyle operatorname {Tanc} left (z right) = left (1 - { frac {7} {51}} , {z} ^ {2} + { frac {1} {255} } , {z} ^ {4} - { frac {2} {69615}} , {z} ^ {6} + { frac {1} {34459425}} , {z} ^ {8} right) left (1 - { frac {8} {17}} , {z} ^ {2} + { frac {7} {255}} , {z} ^ {4} - { frac {4} {9945}} , {z} ^ {6} + { frac {1} {765765}} , {z} ^ {8} right) ^ {- 1}}$

Галерея

Танк абс комплекс 3D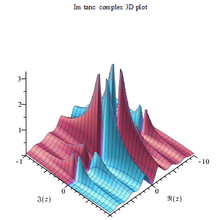

Tanc Im сложный 3D сюжет

Tanc Re сложный 3D сюжет

Смотрите также

• Функция sinhc
• Функция Tanhc
• Функция Coshc

использованная литература