Тепловое моделирование интегральных схем - Thermal simulations for integrated circuits

Миниатюризация компонентов всегда была основной целью полупроводник промышленность, потому что это снижает производственные затраты и позволяет компаниям создавать компьютеры и другие устройства меньшего размера. Однако миниатюризация увеличила рассеиваемую мощность на единицу площади и сделала ее ключевым ограничивающим фактором в Интегральная схема спектакль. Повышение температуры становится актуальным для проводов с относительно небольшим поперечным сечением, где оно может повлиять на нормальное поведение полупроводников. Кроме того, поскольку выделение тепла пропорционально частоте работы схем переключения, быстрые компьютеры выделяют больше тепла, чем медленные, что нежелательно для производителей микросхем. В этой статье обобщаются физические концепции, описывающие генерацию и теплопроводность в интегральной схеме, и представлены численные методы, моделирующие теплопередачу с макроскопической точки зрения.

Производство и передача тепла

Закон Фурье

На макроскопическом уровне Закон Фурье устанавливает связь между теплопередачей в единицу времени на единицу площади и градиентом температуры:

${displaystyle q = -kappa abla T}$

Где ${displaystyle kappa}$ - теплопроводность, [Вт · м⁻¹ K⁻¹].

Джоулевое нагревание

Электронные системы работают на основе сигналов тока и напряжения. Ток - это поток заряженных частиц через материал, и эти частицы (электроны или дырки) взаимодействуют с решеткой кристалла, теряя свою энергию, которая выделяется в виде тепла. Джоулевое нагревание является преобладающим механизмом тепловыделения в интегральных схемах.^[1] и в большинстве случаев является нежелательным эффектом. Для омического материала он имеет вид:

${displaystyle Q = j ^ {2} ho}$

Где ${displaystyle j}$ - плотность тока в [А · м⁻²], ${displaystyle ho}$ - удельное электрическое сопротивление в [${displaystyle {Omega}}$· М] и ${displaystyle Q}$ - количество выделяемого тепла на единицу объема в [Вт · м⁻³].^[1]

Уравнение теплопередачи

Основное уравнение физики теплопередача Задача связывает поток тепла в пространстве, его изменение во времени и выработку энергии следующим выражением:

${displaystyle abla left (каппа слева (Tight) abla Tight) + g = ho C {frac {partial T} {partial t}}}$

Где ${displaystyle kappa}$ - теплопроводность, ${displaystyle ho}$ - плотность среды, ${displaystyle C}$ - удельная теплоемкость, ${displaystyle alpha = {frac {kappa} {ho C}}}$, температуропроводность и ${displaystyle g}$ - скорость тепловыделения на единицу объема. Тепло распространяется от источника в соответствии с приведенным выше уравнением, и решение в однородной среде следует распределению Гаусса.

Методы решения уравнения теплопроводности

Преобразование Кирхгофа

Чтобы избавиться от температурной зависимости ${displaystyle kappa}$, Преобразование Кирхгофа может быть выполнено ^[2]

${displaystyle heta = T_ {s} + {frac {1} {kappa _ {s}}} int _ {T_ {s}} ^ {T} kappa (T) dT}$

куда ${displaystyle kappa _ {s} = kappa left (T_ {s} ight)}$ и ${displaystyle T_ {s}}$ - температура радиатора. При применении этого преобразования уравнение теплопроводности принимает следующий вид:

${displaystyle alpha abla ^ {2} heta + {frac {alpha} {kappa _ {s}}} g = {frac {partial heta} {partial t}}}$

куда ${displaystyle alpha = {frac {kappa} {ho C}}}$ называется коэффициентом диффузии,^[2] что также зависит от температуры. Чтобы полностью линеаризовать уравнение, используется второе преобразование:

${displaystyle alpha _ {s} au = int _ {0} ^ {t} alpha (heta) dt}$

что дает выражение:

${displaystyle abla ^ {2} heta - {frac {1} {alpha _ {s}}} {frac {partial heta} {partial au}} = - {frac {g} {kappa _ {s}}}}$

Простое прямое применение этого уравнения требует приближения. Дополнительные члены, возникающие в преобразованном лапласиане, опускаются, оставляя лапласиан в его обычной форме.^[2]

Аналитические решения

Хотя аналитические решения можно найти только для конкретных и простых случаев, они дают хорошее представление о более сложных ситуациях. Аналитические решения для обычных подсистем также можно комбинировать для получения подробных описаний сложных структур. В работе профессора Бэтти^[2] разложение в ряд Фурье по температуре в области Лапласа вводится для нахождения решения линеаризованного уравнения теплопроводности.

Пример

Эту процедуру можно применить к простому, но нетривиальному случаю: однородный кубический штамп из GaAs, L = 300 мкм. Цель состоит в том, чтобы найти распределение температуры на верхней поверхности. Верхняя поверхность разбита на более мелкие квадраты с индексом i = 1 ... N. Один из них считается источником.

Преобразование Лапласа в уравнение теплопроводности:

${displaystyle abla ^ {2} {ar {Theta}} - {frac {s} {k_ {s}}} {ar {Theta}} = 0}$

куда ${displaystyle {overline {Theta}} = s heta - heta left (au = 0ight)}$

Функция ${displaystyle {overline {Theta}}}$ раскладывается по косинусным функциям для ${displaystyle x}$ и ${displaystyle y}$ переменных и в терминах гиперболических косинусов и синусов для ${displaystyle z}$ Переменная. Затем, применяя адиабатические граничные условия на боковых стенках и фиксируя температуру внизу (температуру радиатора), выводится матричное уравнение теплового импеданса:

${displaystyle Delta heta _ {i} = sum _ {j = 1} ^ {N} R_ {TH_ {ij}} (t) P_ {j} (t)}$

Где индекс ${displaystyle j}$ учитывает источники энергии, а индекс ${displaystyle i}$ относится к каждой небольшой области.

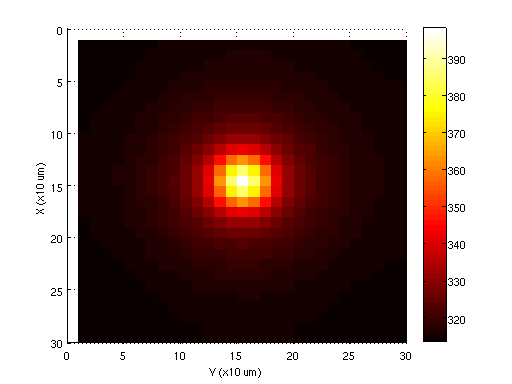
Для получения дополнительных сведений о выводе см. Статью профессора Бэтти.^[2]На рисунке ниже показано распределение температуры в установившемся режиме этого аналитического метода для кубической матрицы размером 300 мкм. Источник постоянной мощности 0,3 Вт подается на центральную поверхность размером 0,1 x 0,1 литра. Как и следовало ожидать, распределение затухает по мере приближения к границам, его максимум находится в центре и почти достигает 400K.

Численные решения

Численные решения используют сетку конструкции для выполнения моделирования. Самые популярные методы: Метод конечных разностей во временной области (FDTD), Метод конечных элементов (FEM) и метод моментов (MoM).

Метод конечных разностей во временной области (FDTD) - это надежный и популярный метод, который заключается в численном решении дифференциальных уравнений, а также в некоторых граничных условиях, определенных задачей. Это делается путем дискретизации пространства и времени и использования формул конечных производных, таким образом, дифференциальные уравнения в частных производных, которые описывают физику проблемы, могут быть решены численно с помощью компьютерных программ.

FEM также представляет собой численную схему, используемую для решения инженерных и математических задач, описываемых дифференциальными уравнениями, а также граничными условиями. Он разбивает пространство на более мелкие элементы, для которых базовые функции назначаются их узлам или ребрам. Базисные функции - это линейные многочлены или полиномы более высокого порядка. Применяя дифференциальное уравнение и граничные условия задачи к базисным функциям, формулируется система уравнений с использованием либо Ритц или же Метод Галеркина. Наконец, для решения системы линейных уравнений используется прямой или итерационный метод.^[3] Для теплового случая больше подходит метод конечных элементов из-за нелинейного характера тепловых свойств.

Пример

Предыдущий пример можно решить численным методом. В этом случае куб можно разбить на прямоугольные элементы. Его базисные функции могут быть выбраны как аппроксимация первого порядка (линейная):

${displaystyle N_ {i} ^ {e} = {frac {1} {2}} xi left (1mp дзета-полет), qquad i = 1,4}$

${displaystyle N_ {i} ^ {e} = {frac {1} {2}} eta left (1mp дзета-полет), qquad i = 2,5}$

${displaystyle N_ {i} ^ {e} = {frac {1} {2}} left (1-xi -eta ight) left (1mp zeta ight), qquad i = 3,6}$

куда ${displaystyle zeta = 2 (z-z_ {c}) / h_ {z}}$. Если ${displaystyle z_ {c} = 0}$, тогда ${displaystyle zeta = 2z / h_ {z}}$.

Используя эти базисные функции и применив метод Галеркина к уравнению теплопередачи, получается матричное уравнение:

${displaystyle left [Sight] left {heta ight} + left [Right] {frac {d} {dt}} left {heta ight} = left {Bight}}$

куда,

${displaystyle R_ {ij} = int _ {v} N_ {j} N_ {i} dV}$

${displaystyle S_ {ij} = kint _ {v} abla N_ {j} .abla N_ {i} dV}$

${displaystyle B_ {i} = {frac {k} {kappa _ {s}}} int _ {Omega _ {1}} N_ {i} p (x, y) dOmega + {frac {k} {kappa _ { s}}} int _ {v} N_ {i} gdV-kT_ {o} sum _ {j = 0} ^ {N_ {D}} int _ {v} abla N_ {j} ^ {D} .abla N_ {i} dV}$.

Эти выражения можно оценить с помощью простого кода МКЭ. Подробнее см.^[3] На рисунке ниже показано распределение температуры для случая численного решения. Это решение очень хорошо согласуется с аналитическим случаем, его пик также достигает 390 К в центре. Очевидное отсутствие гладкости распределения происходит из-за аппроксимации базисных функций первого порядка, и это можно решить, используя базисные функции более высокого порядка. Кроме того, лучшие результаты могут быть получены при использовании более плотной сетки структуры; однако для очень плотных сеток время вычислений сильно увеличивается, что делает моделирование непрактичным.

На следующем рисунке показано сравнение максимальной температуры как функции времени для обоих методов. Система достигает устойчивого состояния примерно через ${displaystyle 1ms}$.

Снижение заказа модели

Численные методы, такие как FEM или FDM, выводят матричное уравнение, как показано в предыдущем разделе. Чтобы решить это уравнение быстрее, метод под названием Снижение заказа модели можно использовать для нахождения приближения более низкого порядка. Этот метод основан на том, что многомерный вектор состояния принадлежит низкоразмерному подпространству [1].

На рисунке ниже показана концепция приближения MOR: найдя матрицу V, размерность системы можно уменьшить, чтобы решить упрощенную систему.

Следовательно, исходная система уравнений:

${displaystyle Cleft {xight} '+ Kleft {xight} = Fleft {uight}}$

становится:

${displaystyle V ^ {T} CVleft {zight} '+ V ^ {T} KVleft {zight} = V ^ {T} Fleft {uight}}$

Чей порядок намного ниже, чем в оригинале, что делает вычисления намного дешевле. Как только решение получено, исходный вектор находится путем взятия произведения на V.

Вывод

Выделение тепла в основном происходит за счет джоулева нагрева, этот нежелательный эффект ограничивает производительность интегральных схем. В готовой статье описана теплопроводность и представлены аналитические и численные методы решения задачи теплопередачи. С использованием этих методов было вычислено установившееся распределение температуры, а также пиковая температура как функция времени для кубической матрицы. Для входной мощности ${displaystyle 0,3 Вт}$ (или же ${displaystyle 3.333e8W / m_ {2}}$), нанесенного на один поверхностный источник на вершине кубической матрицы, было вычислено пиковое приращение температуры порядка 100 К. Такое повышение температуры может повлиять на поведение окружающих полупроводниковых устройств. Кардинально меняются такие важные параметры, как мобильность. Вот почему рассеивание тепла является актуальной проблемой, и ее необходимо учитывать при проектировании схем.

Смотрите также

• Выработка тепла в интегральных схемах

Рекомендации