Слабосвязанная матрица с диагональным преобладанием - Википедия - Weakly chained diagonally dominant matrix
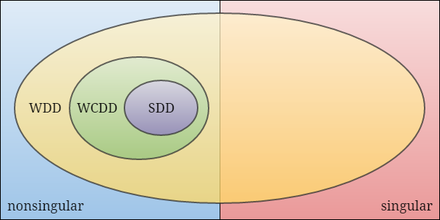
В математике слабосвязанные матрицы с диагональным преобладанием семья невырожденные матрицы которые включают строго матрицы с диагональным преобладанием.
Определение
Предварительные мероприятия
Мы говорим ряд сложной матрицы является строго по диагонали (SDD) если . Мы говорим является SDD, если все его строки являются SDD. Слабо доминирующая по диагонали (WDD) определяется как вместо.
В ориентированный граф связанный с комплексная матрица задается вершинами и ребра определяются следующим образом: существует ребро из если и только если .
Определение
Комплексная квадратная матрица как говорят слабо сцепленный по диагонали (WCDD), если
- это WDD и
- для каждой строки то есть нет SDD, существует ходить в ориентированном графе заканчивается строкой SDD .
Пример

В матрица
это WCDD.
Характеристики
Неособенность
Матрица WCDD невырожденна.[1]
Доказательство:[2]Позволять - матрица WCDD. Предположим, что существует ненулевое в нулевом пространстве . Без ограничения общности пусть быть таким, чтобы для всех .С это WCDD, мы можем прогуляться заканчивается строкой SDD .
Взяв модули по обе стороны от
и применяя неравенство треугольника, получаем
и, следовательно, строка не SDD. Более того, поскольку является WDD, указанная выше цепочка неравенств выполняется с равенством, так что в любое время .Следовательно, . Повторяя этот аргумент с , и т. д., мы находим, что не SDD, противоречие.
Напоминая, что несводимый Матрица - это матрица, чей связанный ориентированный граф сильно связанный, тривиальным следствием вышеизложенного является то, что неприводимо диагонально доминирующая матрица (т.е. неприводимая матрица WDD хотя бы с одной строкой SDD) невырождена.[3]
Связь с невырожденными M-матрицами
Следующие варианты эквивалентны:[4]
Фактически изучались L-матрицы WCDD ( Джеймс Х. Брамбл и Б. Э. Хаббард) еще в 1964 г. в журнальной статье[5] в котором они появляются под альтернативным именем матрицы положительного типа.
Более того, если является WCDD L-матрицу, мы можем оценить ее обратную следующим образом:[6]
- куда
Обратите внимание, что всегда равен нулю и что правая часть приведенной выше оценки равна всякий раз, когда одна или несколько констант является одним.
Известны более жесткие оценки для обратной L-матрицы WCDD.[7][8][9][10]
Приложения
Из-за их отношений с М-матрицы (видеть над ), Матрицы WCDD часто встречаются в практических приложениях, пример приведен ниже.
Монотонные числовые схемы
L-матрицы WCDD естественным образом возникают из схем монотонной аппроксимации для уравнения в частных производных.
Например, рассмотрим одномерный Проблема Пуассона
- за
с Граничные условия Дирихле .Пусть числовая сетка (для некоторых положительных делит единицу), монотонная разностная схема для задачи Пуассона принимает вид
- куда
и
Обратите внимание, что является L-матрицей WCDD.
Рекомендации
- ^ Shivakumar, P.N .; Чу, Ким Хо (1974). «Достаточное условие отличия от нуля детерминант» (PDF). Труды Американского математического общества. 43 (1): 63. Дои:10.1090 / S0002-9939-1974-0332820-0. ISSN 0002-9939.
- ^ Азимзаде, Парсиад; Форсайт, Питер А. (2016). «Слабо связанные матрицы, итерация политики и импульсный контроль». Журнал SIAM по численному анализу. 54 (3): 1341–1364. arXiv:1510.03928. Дои:10.1137 / 15M1043431. ISSN 0036-1429.
- ^ Хорн, Роджер А .; Джонсон, Чарльз Р. (1990). «Матричный анализ». Издательство Кембриджского университета, Кембридж. Цитировать журнал требует
| журнал =(помощь) - ^ Азимзаде, Парсиада (2019). «Быстрый и стабильный тест для проверки того, является ли матрица со слабым диагональным доминированием невырожденной M-матрицей». Математика вычислений. 88 (316): 783–800. arXiv:1701.06951. Bibcode:2017arXiv170106951A. Дои:10.1090 / mcom / 3347.
- ^ Брамбл, Джеймс Х .; Хаббард, Б. Э. (1964). «О конечно-разностном аналоге эллиптической задачи, которая не является ни диагонально доминирующей, ни неотрицательной». Журнал математической физики. 43: 117–132. Дои:10.1002 / sapm1964431117.
- ^ Shivakumar, P.N .; Уильямс, Джозеф Дж .; Е, Цян; Маринов, Корнелиу А. (1996). «О двусторонних границах, связанных со слабо диагонально доминирующими M-матрицами, применительно к динамике цифровых схем». Журнал SIAM по матричному анализу и приложениям. 17 (2): 298–312. Дои:10.1137 / S0895479894276370. ISSN 0895-4798.
- ^ Ченг, Гуан-Хуэй; Хуан, Тинг-Чжу (2007). "Верхняя граница для строго диагонально доминирующих M-матриц ". Линейная алгебра и ее приложения. 426 (2–3): 667–673. Дои:10.1016 / j.laa.2007.06.001. ISSN 0024-3795.
- ^ Ли, Вэнь (2008). "Бесконечная норма нормы для обратной невырожденной диагональной доминирующей матрицы". Письма по прикладной математике. 21 (3): 258–263. Дои:10.1016 / j.aml.2007.03.018. ISSN 0893-9659.
- ^ Ван, Пинг (2009). "Верхняя граница для строго диагонально доминирующих M-матриц ". Линейная алгебра и ее приложения. 431 (5–7): 511–517. Дои:10.1016 / j.laa.2009.02.037. ISSN 0024-3795.
- ^ Хуанг, Тин-Чжу; Чжу, Ян (2010). "Оценка для слабо сцепленных M-матриц с диагональным преобладанием ". Линейная алгебра и ее приложения. 432 (2–3): 670–677. Дои:10.1016 / j.laa.2009.09.012. ISSN 0024-3795.



























![{ displaystyle left Vert A ^ {- 1} right Vert _ { infty} leq sum _ {i} left [a_ {ii} prod _ {j = 1} ^ {i} ( 1-u_ {j}) right] ^ {- 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cde4e6b1c1dfa2bf86f33f7da201fe0632353a0c)










![{ displaystyle [{ vec {g}}] _ {j} = g (jh)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/884cee0f59a4246e30d947ba57c3514382370131)

