Рыскание (вращение) - Википедия - Yaw (rotation)

Рыскание, тангаж и крен в самолете

Движение по рысканью в самолете

Мнемоника для запоминания названий углов

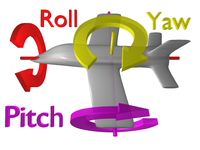
А вращение по рысканью движение вокруг ось рыскания твердого тела, которое меняет направление, на которое указывает, влево или вправо от направления движения. В скорость рыскания или же скорость рыскания автомобиля, самолета, снаряда или другого твердого тела является угловая скорость этого поворота, или скорость изменения угла курса, когда самолет находится в горизонтальном положении. Обычно он измеряется в градусах в секунду или радианах в секунду.

Еще одно важное понятие - рыскание. момент, или момент рыскания, который является составляющей крутящий момент относительно оси рыскания.

Измерение

Скорость рыскания можно измерить путем измерения скорости относительно земли в двух геометрически разделенных точках на теле, или с помощью гироскоп, или его можно синтезировать из акселерометры и тому подобное. Это основная мера того, как водители визуально ощущают поворот автомобиля.

Оси корабля и вращения вокруг них

Это важно в электронный стабилизированный транспортных средств. Скорость рыскания напрямую связана с поперечным ускорением автомобиля, поворачивающего с постоянной скоростью вокруг постоянного радиуса, соотношением

тангенциальная скорость * скорость рыскания = боковое ускорение = тангенциальная скорость ^ 2 / радиус поворота в соответствующих единицах

Знаковое соглашение может быть установлено путем пристального внимания к системам координат.

В более общем маневрировать где изменяется радиус и / или изменяется скорость, указанное выше соотношение больше не выполняется.

Контроль скорости рыскания

Скорость рыскания можно измерить акселерометрами по вертикальной оси. Любое устройство, предназначенное для измерения скорости рыскания, называется датчик скорости рыскания.

Дорожная техника

Изучение устойчивости дорожного транспортного средства требует разумного приближения к уравнениям движения.

Динамика дорожного транспортного средства

На схеме изображен четырехколесный автомобиль, в котором расположена передняя ось. а метров впереди центр тяжести а задняя ось б метров назад от центра тяжести. Кузов автомобиля указывает в направлении ${ displaystyle theta}$ (тета) пока он движется в направлении ${ displaystyle psi}$ (фунт / кв. дюйм). В общем, это не одно и то же. Протектор шины проходит в области точки контакта в направлении движения, но ступицы выровнены с кузовом автомобиля, при этом рулевое управление занимает центральное место. Шины деформируются при вращении, компенсируя это смещение, и, как следствие, создают боковые силы.

Из курсовая устойчивость исследование, обозначающее угловую скорость ${ displaystyle omega}$, уравнения движения:

${ displaystyle { frac {d omega} {dt}} = 2k { frac {(ab)} {I}} beta -2k { frac {(a ^ {2} + b ^ {2}) } {VI}} omega}$

${ displaystyle { frac {d beta} {dt}} = - { frac {4k} {MV}} beta + (1-2k) { frac {(ba)} {MV ^ {2}} } omega}$

Коэффициент ${ displaystyle { frac {d beta} {dt}}}$ будет называться 'демпфирование 'по аналогии с массой-пружиной-демпфером, имеющей аналогичное уравнение движения. По той же аналогии коэффициент при ${ displaystyle beta}$ будет называться «жесткостью», поскольку его функция - возвращать систему к нулевому прогибу так же, как пружина.

Форма раствора зависит только от знаков условий демпфирования и жесткости. На рисунке представлены четыре возможных типа решения.

Единственное удовлетворительное решение требует, чтобы и жесткость, и демпфирование были положительными. Если центр тяжести находится впереди центра колесная база (${ Displaystyle (б> а)}$, он всегда будет положительным, и автомобиль будет устойчивым на всех скоростях. Однако, если он находится дальше на корме, этот член может стать отрицательным выше скорости, определяемой:

${ displaystyle V ^ {2} = { frac {2k (a + b) ^ {2}} {M (a-b)}}}$

Выше этой скорости автомобиль будет двигаться по курсу. неустойчивый. Поправки на относительное влияние передних и задних шин и усилий рулевого управления доступны в основной статье.

Отношения с другими системами ротации

Эти вращения собственное вращение и исчисление за ними похоже на Формулы Френе-Серре. Выполнение поворота в собственной системе отсчета эквивалентно правой умножить его характеристической матрицы (матрицы, имеющего вектор опорного кадра в виде столбцов) на матрицу вращения.

История

Первым самолетом, продемонстрировавшим активное управление по всем трем осям, стал самолет. Планер братьев Райт 1902 года.^[1]

Смотрите также

• Неблагоприятный рыскание
• Главные оси самолета
• Кориолисовое ускорение
• Направленная устойчивость
• Динамика полета
• Шесть степеней свободы
• Динамика автомобиля
• Датчик скорости рыскания

Рекомендации