Нуль-симметричный граф - Zero-symmetric graph

в математический поле теория графов, а нулевой симметричный граф это связный граф в котором каждая вершина имеет ровно три инцидентных ребра, и для каждых двух вершин существует единственное симметрия переводя одну вершину в другую. Такой граф является вершинно-транзитивный граф но не может быть реберно-транзитивный граф: количество симметрий равно количеству вершин, слишком мало, чтобы соединить каждое ребро с каждым другим ребром.[1]
Название для этого класса графов было придумано Р. М. Фостер в письме 1966 г. Х. С. М. Кокстер.[2] Эти графы в настоящее время называются кубическими GRR (графические регулярные представления). [3]
Примеры
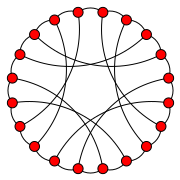
Наименьший нулевой симметричный граф - это неплоский граф с 18 вершинами.[4] Его Обозначение LCF равно [5, −5]9.
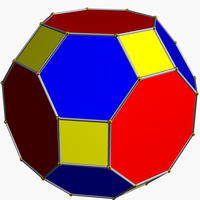
Среди планарные графы, то усеченный кубооктаэдр и усеченные икосододекаэдрические графы также нуль-симметричны.[5]
Все эти примеры двудольные графы. Однако существуют более крупные примеры недвудольных графов с нулевой симметрией.[6]
В этих примерах также есть три разных класса симметрии (орбиты) ребер. Однако существуют нуль-симметричные графы только с двумя орбитами ребер. Наименьший такой граф имеет 20 вершин, причем Обозначение LCF [6,6,-6,-6]5.[7]
Характеристики
Каждый конечный нуль-симметричный граф является Граф Кэли, свойство, которое не всегда выполняется для кубических вершинно-транзитивных графов в более общем смысле, и которое помогает в решении комбинаторное перечисление задачи о нуль-симметричных графах. Имеется 97687 нуль-симметричных графов с числом вершин до 1280. Эти графы составляют 89% кубических графов Кэли и 88% всех связных вершинно-транзитивных кубических графов с одинаковым количеством вершин.[8]
| Нерешенная проблема в математике: Каждый ли конечный нуль-симметричный граф содержит Гамильтонов цикл ? (больше нерешенных задач по математике) |
Все известные конечные связные нуль-симметричные графы содержат Гамильтонов цикл, но неизвестно, обязательно ли каждый конечный связный нуль-симметричный граф гамильтоновым.[9] Это частный случай Гипотеза Ловаса что (за пятью известными исключениями, ни одно из которых не является нулевым симметричным) каждый конечный связный вершинно-транзитивный граф и каждый конечный граф Кэли гамильтонов.
Смотрите также
- Полусимметричный граф, графы, которые имеют симметрии между каждыми двумя ребрами, но не между каждыми двумя вершинами (меняя роли ребер и вершин в определении нуль-симметричных графов)
Рекомендации
- ^ Кокстер, Гарольд Скотт Макдональд; Фрухт, Роберто; Пауэрс, Дэвид Л. (1981), Нуль-симметричные графы, Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], Нью-Йорк-Лондон, ISBN 0-12-194580-4, МИСТЕР 0658666
- ^ Coxeter, Frucht & Powers (1981), п. ix.
- ^ Лаури, Йозеф; Скапеллато, Рафаэле (2003), Темы автоморфизмов и реконструкции графов, Тексты студентов Лондонского математического общества, Cambridge University Press, стр. 20–21, ISBN 9780521529037.
- ^ Coxeter, Frucht & Powers (1981), Рисунок 1.1, стр. 5.
- ^ Coxeter, Frucht & Powers (1981), с. 75 и 80.
- ^ Coxeter, Frucht & Powers (1981), п. 55.
- ^ Кондер, Марстон Д. Э.; Писанский, Томаж; Житник, Арджана (2017), "Вершинно-транзитивные графы и их типы дуги", Ars Mathematica Contemporanea, 12 (2): 383–413, arXiv:1505.02029, Дои:10.26493 / 1855-3974.1146.f96, МИСТЕР 3646702
- ^ Поточник, Примож; Спига, Пабло; Верре, Габриэль (2013), "Кубические вершинно-транзитивные графы с числом вершин до 1280", Журнал символических вычислений, 50: 465–477, arXiv:1201.5317, Дои:10.1016 / j.jsc.2012.09.002, МИСТЕР 2996891.
- ^ Coxeter, Frucht & Powers (1981), п. 10.
