Угловое разрешение (рисунок графика) - Angular resolution (graph drawing)

Этот рисунок граф гиперкуба имеет угловое разрешение π / 4.

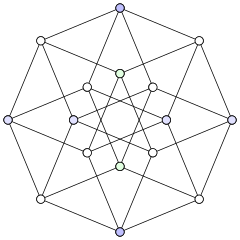
В рисунок графика, то угловое разрешение рисунка графа - это самый острый угол, образованный любыми двумя ребрами, которые встречаются в общей вершине рисунка.

Характеристики

Отношение к степени вершины

Formann et al. (1993) заметил, что каждый прямой рисунок графика с максимальной степенью d имеет угловое разрешение не более 2π /d: если v является вершиной степени d, то ребра, инцидентные v разделить пространство вокруг v в d клинья с общим углом 2π, и самый маленький из этих клиньев должен иметь угол не более 2π /d. Более того, если граф d-обычный, он должен иметь угловое разрешение менее ${ displaystyle { frac { pi} {d-1}}}$, потому что это лучшее разрешение, которое может быть достигнуто для вершины на выпуклый корпус чертежа.

Связь с раскраской графа

В качестве Formann et al. (1993) показал, что максимально возможное угловое разрешение графика грамм тесно связан с хроматическое число из квадрат грамм², граф на том же множестве вершин, в котором пары вершин соединены ребром, если их расстояние в грамм не больше двух. Если грамм² можно раскрасить χ цвета, тогда грамм можно рисовать с угловым разрешением π /χ - ε, для любого ε> 0, назначив разные цвета вершинам обычный χ-угольник и поместив каждую вершину грамм близко к вершине многоугольника того же цвета. Используя эту конструкцию, они показали, что каждый граф с максимальной степенью d имеет рисунок с угловым разрешением, пропорциональным 1/d². Эта граница близка к жесткой: они использовали вероятностный метод для доказательства существования графов максимальной степени d чьи рисунки имеют угловое разрешение ${ displaystyle O left ({ frac { log d} {d ^ {2}}} right)}$.

Наличие оптимальных чертежей

Formann et al. (1993) предоставил пример, показывающий, что существуют графики, на которых отсутствует рисунок, обеспечивающий максимально возможное угловое разрешение; вместо этого у этих графиков есть семейство чертежей, угловое разрешение которых стремится к некоторому предельному значению, но не достигает его. В частности, они продемонстрировали граф с 11 вершинами, на котором есть чертежи углового разрешения. π / 3 - ε для любого ε> 0, но у которого нет чертежа углового разрешения точно π / 3.

Специальные классы графов

Деревья

Каждое дерево может быть нарисовано таким образом, чтобы рёбра располагались на равных расстояниях вокруг каждой вершины, это свойство известно как идеальное угловое разрешение. Более того, если ребра могут быть свободно переставлены вокруг каждой вершины, то такой чертеж возможен без пересечений, со всеми ребрами единичной длины или выше, и с размещением всего чертежа в пределах Ограничительная рамка полинома площадь. Однако, если циклическое упорядочение ребер вокруг каждой вершины уже определено как часть входных данных проблемы, то для достижения идеального углового разрешения без пересечений иногда может потребоваться экспоненциальная площадь.^[1]

Внешнепланарные графы

Идеальное угловое разрешение не всегда возможно для внешнепланарные графы, потому что вершины на выпуклой оболочке чертежа со степенью больше единицы не могут иметь инцидентные ребра, равномерно расположенные вокруг них. Тем не менее, каждый внешнепланарный граф максимальной степени d имеет внешнепланарный чертеж с угловым разрешением, пропорциональным 1/d.^[2]

Планарные графики

За планарные графы с максимальной степенью d, техника квадратного раскраски Formann et al. (1993) обеспечивает чертеж с угловым разрешением, пропорциональным 1/d, поскольку квадрат плоского графа должен иметь хроматическое число, пропорциональное d. Точнее, Вегнер в 1977 году предположил, что хроматическое число квадрата плоского графа не превосходит ${ displaystyle max left (d + 5, { frac {3d} {2}} + 1 right)}$, и известно, что хроматическое число не превышает ${ displaystyle { frac {5d} {3}} + O (1)}$.^[3] Однако рисунки, полученные с помощью этой техники, обычно не являются плоскими.

Для некоторых планарных графиков оптимальное угловое разрешение плоского прямолинейного чертежа составляет O (1 /d³), куда d - степень графа.^[4] Кроме того, на таком чертеже могут быть вынуждены использовать очень длинные края, более длинные на экспоненциальный коэффициент, чем самые короткие края на чертеже.Малиц и Папакостас (1994) использовал теорема об упаковке кругов и кольцевая лемма чтобы показать, что каждый планарный граф с максимальной степенью d имеет планарный рисунок, угловое разрешение которого в худшем случае является экспоненциальной функцией d, независимо от количества вершин в графе.

Вычислительная сложность

NP-сложно определить, является ли данный граф максимальной степени d имеет рисунок с угловым разрешением 2π /d, даже в частном случае, когда d = 4.^[5] Однако для некоторых ограниченных классов рисунков, включая рисунки деревьев, в которых расширение листьев до бесконечности дает выпуклое подразделение плоскости, а также рисунки планарных графов, в которых каждая ограниченная грань представляет собой центрально-симметричный многоугольник, рисунок оптимального угловое разрешение можно найти в полиномиальное время.^[6]

История

Угловое разрешение было впервые определено Formann et al. (1993).

Хотя первоначально он был определен только для прямолинейных чертежей графов, более поздние авторы также исследовали угловое разрешение чертежей, на которых ребра представляют собой многоугольные цепи.^[7] дуги окружности,^[8] или сплайновые кривые.^[9]

Угловое разрешение графика тесно связано с его разрешением пересечения, угол, образованный переходы на чертеже графика. Особенно, Чертеж RAC стремится к тому, чтобы все эти углы прямые углы, максимально возможный угол пересечения.^[10]

Примечания

Рекомендации