Прямой угол - Right angle


В геометрия и тригонометрия, а прямой угол является угол ровно 90° (градусы),[1] соответствует четверти повернуть.[2] Если луч размещается так, чтобы его конец находился на прямой и прилегающие углы были равны, тогда они прямые.[3] Срок - это калька из латинский angulus rectus; Вот прямая мышца означает «вертикально», имея в виду вертикальный перпендикуляр к горизонтальной базовой линии.
Тесно связанные и важные геометрические концепции: перпендикуляр линии, то есть линии, образующие прямые углы в точке пересечения, и ортогональность, которое является свойством образовывать прямые углы, обычно применяемые к векторов. Наличие прямого угла в треугольник является определяющим фактором для прямоугольные треугольники,[4] сделать правильный угол основой тригонометрии.
Этимология
Значение «прямо» в «прямом угле», возможно, относится к латинский прилагательное прямая мышца, который может быть переведен на прямой, прямой, вертикальный или перпендикулярный. А Греческий эквивалент Ортопеды, что значит прямой или же перпендикуляр (видеть ортогональность ).
В элементарной геометрии
А прямоугольник это четырехугольник с четырьмя прямыми углами. А квадрат имеет четыре прямых угла в дополнение к сторонам равной длины.
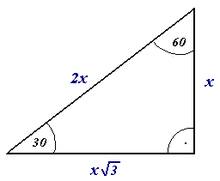
В теорема Пифагора заявляет, как определить, когда треугольник прямоугольный треугольник.
Символы

В Unicode, символ прямого угла U + 221F ∟ ПРЯМОЙ УГОЛ (HTML∟ · & angrt;). Его не следует путать с символом аналогичной формы U + 231E ⌞ НИЖНИЙ ЛЕВЫЙ УГОЛ (HTML⌞ · & dlcorn ;, & llcorner;). Связанные символы U + 22BE ⊾ ПРАВЫЙ УГОЛ С ДУГОМ (HTML⊾ · & angrtvb;), U + 299C ⦜ ВАРИАНТ ПРЯМОГО УГОЛА С ПЛОЩАДЬЮ (HTML⦜ · & vangrt;), и U + 299D ⦝ ИЗМЕРЕННЫЙ ПРАВЫЙ УГОЛ С ТОЧКОЙ (HTML⦝ · & angrtvbd;).[5]
На диаграммах тот факт, что угол является прямым углом, обычно выражается добавлением небольшого прямого угла, который образует квадрат с углом на диаграмме, как показано на диаграмме прямоугольного треугольника (в британском английском: прямоугольный треугольник) вправо. Символ измеренного угла, дуга с точкой, используется в некоторых европейских странах, в том числе в немецкоязычных странах и Польше, в качестве альтернативного символа прямого угла.[6]
Евклид
Прямые углы важны в Элементы Евклида. Они определены в Книге 1, определение 10, в котором также определены перпендикулярные линии. Определение 10 не использует числовые измерения в градусах, а касается самой сути того, что такое прямой угол, а именно двух прямых линий, пересекающихся с образованием двух равных и смежных углов.[7] Прямые, образующие прямые углы, называются перпендикулярными.[8] Евклид использует прямые углы в определениях 11 и 12 для определения острых углов (меньших прямого угла) и тупых углов (тех, которые больше прямого).[9] Два угла называются дополнительный если их сумма - прямой угол.[10]
Книга 1 Постулат 4 гласит, что все прямые углы равны, что позволяет Евклиду использовать прямой угол как единицу измерения других углов. Комментатор Евклида Прокл дал доказательство этого постулата, используя предыдущие постулаты, но можно утверждать, что это доказательство использует некоторые скрытые предположения. Саккери также дал доказательство, но с более явным предположением. В Гильберта с аксиоматизация геометрии это утверждение дается как теорема, но только после серьезной работы. Кто-то может возразить, что, даже если постулат 4 может быть доказан на основе предыдущих, в том порядке, в котором Евклид представляет свой материал, необходимо включить его, поскольку без него постулат 5, который использует прямой угол в качестве единицы измерения, не дает смысл.[11]
Преобразование в другие единицы
Прямой угол может быть выражен в разных единицах:
- 1/4 повернуть
- 90° (градусы )
- π/2 радианы или же τ/4 рад
- 100 град (также называемый оценка, Градиан, или же гон)
- 8 баллов (из 32 баллов картушка )
- 6 часов (астрономический часовой угол )
Правило 3-4-5
На протяжении всей истории плотники и каменщики знали быстрый способ проверить, является ли угол истинным «прямым». Он основан на наиболее широко известных Пифагорейская тройка (3, 4, 5) и так называемое «правило 3-4-5». Если под рассматриваемым углом провести прямую линию вдоль одной стороны ровно на 3 единицы длины, а вдоль второй стороны ровно на 4 единицы длины, получится гипотенуза (более длинная линия напротив прямого угла, соединяющая две измеренные конечные точки) длиной ровно 5 единиц. Это измерение может быть выполнено быстро и без технических инструментов. Геометрический закон, лежащий в основе измерения, - это теорема Пифагора («Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов двух смежных сторон»).
Теорема Фалеса
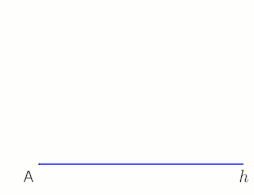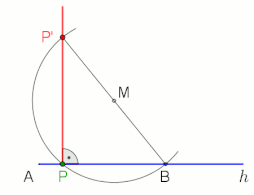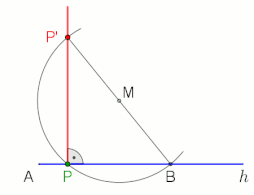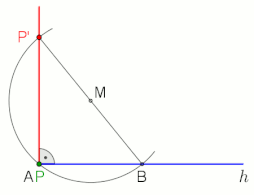

анимация в конце с паузой 10 с
Теорема Фалеса утверждает, что угол, вписанный в полукруг (с вершиной на полукруге и определяющими лучами, проходящими через концы полукруга) - прямой угол.
Два примера применения, в которые включены прямой угол и теорема Фалеса (см. Анимацию).
Смотрите также
Рекомендации
- ^ "Прямой угол". Открытый справочник по математике. Получено 26 апреля 2017.
- ^ Вентворт п. 11
- ^ Wentworth p. 8
- ^ Wentworth p. 40
- ^ Таблицы кодов символов Unicode 5.2 Математические операторы, Разные математические символы-B
- ^ Мюллер-Филипп, Сюзанна; Горски, Ханс-Иоахим (2011). Leitfaden Geometrie [Справочник по геометрии] (на немецком). Springer. ISBN 9783834886163.
- ^ Хит п. 181
- ^ Хит п. 181
- ^ Хит п. 181
- ^ Wentworth p. 9
- ^ Хит, стр. 200-201 для абзаца
- Вентворт, Г.А. (1895). Учебник геометрии. Джинн и Ко.
- Евклид, комментарий и пер. к Т. Л. Хит Элементы Vol. 1 (1908 г., Кембридж) Google Книги
