Дуговая диаграмма - Википедия - Arc diagram

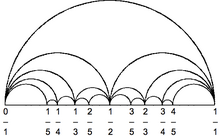
В рисунок графика, дуговая диаграмма это стиль рисования графа, в котором вершины графа размещаются вдоль линии в Евклидова плоскость, с краями, нарисованными как полукруги в одной из двух полуплоскостей, ограниченных линией, или в виде гладких кривых, образованных последовательностями полукругов. В некоторых случаях линейные сегменты самой линии также допускаются в качестве ребер, если они соединяют только вершины, идущие подряд вдоль линии.
Использование фразы «дуговая диаграмма» для такого рода рисунков следует за использованием аналогичного типа диаграммы. Ваттенберг (2002) чтобы визуализировать шаблоны повторения в строках, используя дуги для соединения пар равных подстрок. Однако этот стиль рисования графиков намного старше своего названия и восходит к работам Саати (1964) и Николсон (1968), который использовал дуговые диаграммы для изучения числа пересечений графиков. Более старое, но реже используемое название для дуговых диаграмм - линейные вложения.[1]
Хир, Босток и Огиевецкий (2010) напишите, что дуговые диаграммы «могут не передавать общую структуру графа так же эффективно, как двухмерная компоновка», но что их компоновка позволяет легко отображать многомерные данные, связанные с вершинами графа.
Планарные графики
В качестве Николсон (1968) Как видно, каждое вложение графа в плоскость можно деформировать в дуговую диаграмму, не меняя числа пересечений. В частности, каждый планарный граф имеет плоскую дуговую диаграмму. Однако для этого вложения может потребоваться использовать более одного полукруга для некоторых его краев.
Если граф нарисован без пересечений с использованием дугообразной диаграммы, в которой каждое ребро представляет собой один полукруг, то рисунок будет двухстраничным. вложение книги, то, что возможно только для субгамильтоновы графы, подмножество плоских графов.[2] Например, максимальный планарный граф имеет такое вложение тогда и только тогда, когда оно содержит Гамильтонов цикл. Следовательно, негамильтонов максимальный планарный граф, такой как График Гольднера – Харари не может иметь плоского вложения с одним полукругом на ребро. Проверка того, имеет ли данный граф дуговую диаграмму этого типа без перекрестков (или, что эквивалентно, имеет ли он номер страницы два), является НП-полный.[3]
Однако у каждого плоского графа есть дуговая диаграмма, в которой каждое ребро изображено как biarc не более двух полукругов. Более того, каждый ул-планарный ориентированный граф (плоский ориентированный ациклический граф с одним источником и одним стоком, оба на внешней поверхности) имеет дуговую диаграмму, на которой каждое ребро образует монотонную кривую, причем все эти кривые последовательно ориентированы от одного конца линии вершины к другому.[4] Для неориентированных плоских графов один из способов построить дуговую диаграмму с не более чем двумя полукругами на ребро - разделить граф и добавить дополнительные ребра, чтобы получившийся граф имел Гамильтонов цикл (и так, чтобы каждое ребро подразделялось не более одного раза), и использовать порядок вершин на гамильтоновом цикле как порядок вдоль прямой.[5]
Минимизация переходов
Поскольку проверка того, имеет ли данный граф дуговую диаграмму с одним полукругом на ребро и без пересечений, является NP-полной, это также NP-жесткий найти дуговую диаграмму этого типа, минимизирующую количество пересечений. Эта задача минимизации пересечения остается NP-трудной для неплоских графов, даже если порядок вершин вдоль прямой фиксирован.[1] Однако в случае фиксированного порядка вложение без пересечений (если таковое существует) может быть найдено за полиномиальное время, переведя задачу в 2-выполнимость Задача, в которой переменные представляют размещение каждой дуги, а ограничения не позволяют размещать пересекающиеся дуги с одной стороны от линии вершины.[6] Кроме того, в случае фиксированного порядка вложение, минимизирующее пересечение, может быть приблизительный решив максимальный разрез проблема во вспомогательном графе, который представляет полукруги и их потенциальные пересечения (или, что эквивалентно, аппроксимируя версию MAX2SAT экземпляра 2-выполнимости).[7]
Цимиковски и Шоп (1996), Цимиковский (2002), и Он, Сикора и Врт'о (2005) обсудить эвристику для поиска дуговых диаграмм с небольшим количеством пересечений.
Ориентация по часовой стрелке
Для рисунков ориентированные графы, общее соглашение состоит в том, чтобы рисовать каждую дугу по часовой стрелке, так что дуги, которые направлены от более ранней вершины к более поздней в последовательности, рисуются над линией вершин, а дуги, направленные от более поздней к более ранней вершине, рисуются ниже линия. Это соглашение об ориентации по часовой стрелке было разработано как часть другого стиля рисования графиков. Fekete et al. (2003), и примененный к дуговым диаграммам Преториус и ван Вейк (2007).
Другое использование
Дуговые диаграммы использовались Брандес (1999) визуализировать диаграмма состояний из регистр сдвига, и по Джиджев и Врт'О (2002) чтобы показать, что номер перехода каждого графа хотя бы квадратичен в своем ширина разреза.
Примечания
- ^ а б Masuda et al. (1990).
- ^ Нанесение полукругов на расположение кромок в вложениях книг уже было выполнено Бернхарт и Кайнен (1979), но явная связь дуговых диаграмм с вложениями двухстраничной книги, по-видимому, связана с Masuda et al. (1990).
- ^ Чанг, Лейтон и Розенберг (1987).
- ^ Джордано и др. (2007).
- ^ Bekos et al. (2013).
- ^ Эфрат, Эртен и Кобуров (2007).
- ^ Чимиковски и Мумей (2007).
Рекомендации
- Бекос, Майкл А .; Кауфманн, Майкл; Кобуров, Стивен Г .; Симвонис, Антониос (2013), "Гладкие ортогональные макеты", Графический рисунок: 20-й Международный симпозиум, GD 2012, Редмонд, Вашингтон, США, 19–21 сентября 2012 г., Исправленные избранные статьи, Конспект лекций по информатике, 7704, Springer, стр. 150–161, Дои:10.1007/978-3-642-36763-2_14, ISBN 978-3-642-36762-5.
- Bernhart, Frank R .; Кайнен, Пол К. (1979), «Книжная толщина графа», Журнал комбинаторной теории, Серия B, 27 (3): 320–331, Дои:10.1016/0095-8956(79)90021-2.
- Брандес, Ульрик (1999), «Охота на График B», Графический рисунок: 7-й Международный симпозиум, GD'99, Замок Штиржин, Чехия, 15–19 сентября 1999 г., Труды, Конспект лекций по информатике, 1731, Springer, стр. 410–415, Дои:10.1007/3-540-46648-7_42, ISBN 978-3-540-66904-3.
- Чунг, Фан Р. К.; Лейтон, Фрэнк Томпсон; Розенберг, Арнольд Л. (1987), «Встраивание графиков в книги: проблема компоновки приложений для проектирования СБИС» (PDF), Журнал SIAM по алгебраическим и дискретным методам, 8 (1): 33–58, Дои:10.1137/0608002.
- Cimikowski, Роберт (2002), "Алгоритмы решения фиксированной линейной проблемы числа пересечений", Дискретная прикладная математика, 122 (1–3): 93–115, Дои:10.1016 / S0166-218X (01) 00314-6, МИСТЕР 1907825.
- Чимиковски, Роберт; Муми, Брендан (2007), "Аппроксимация фиксированного линейного числа пересечений", Дискретная прикладная математика, 155 (17): 2202–2210, Дои:10.1016 / j.dam.2007.05.009, МИСТЕР 2360650.
- Чимиковски, Роберт; Шоп, Пол (1996), "Алгоритм нейронной сети для задачи компоновки графа", IEEE-транзакции в нейронных сетях, 7 (2): 341–345, Дои:10.1109/72.485670, PMID 18255588.
- Джиджев, Христо; Vrt'o, Imrich (2002), "Улучшенная нижняя оценка числа пересечений", Графический рисунок: 9-й Международный симпозиум, GD 2001, Вена, Австрия, 23–26 сентября 2001 г., Исправленные статьи., Конспект лекций по информатике, 2265, Springer, стр. 96–101, Дои:10.1007/3-540-45848-4_8, ISBN 978-3-540-43309-5.
- Эфрат, Алон; Эртен, Цесим; Кобуров, Стивен Г. (2007), "Рисование плоских графов по дуге окружности с фиксированным местоположением", Журнал графических алгоритмов и приложений, 11 (1): 145–164, Дои:10.7155 / jgaa.00140.
- Фекете, Жан-Даниэль; Ван, Дэвид; Данг, Нием; Арис, Алекс; Плезант, Кэтрин (2003), "Наложение ссылок графа на карты деревьев", IEEE Symp. по визуализации информации, Сборник плакатов, стр. 82–83.
- Джордано, Франческо; Лиотта, Джузеппе; Мчедлидзе, Тамара; Симвонис, Антониос (2007), "Вычисление восходящих топологических книжных вложений восходящих плоских орграфов", Алгоритмы и вычисления: 18-й Международный симпозиум, ISAAC 2007, Сендай, Япония, 17-19 декабря 2007 г., Труды, Конспект лекций по информатике, 4835, Springer, стр. 172–183, Дои:10.1007/978-3-540-77120-3_17, ISBN 978-3-540-77118-0.
- Он, Хунмэй; Сикора, Ондрей; Vrt'o, Имрих (2005), «Эвристика минимизации пересечения для двухстраничных рисунков», Электронные заметки по дискретной математике, 22: 527–534, Дои:10.1016 / j.endm.2005.06.088.
- Хеер, Джеффри; Босток, Майкл; Огиевецкий, Вадим (2010), «Экскурсия по зоопарку визуализации», Коммуникации ACM, 53 (6): 59–67, Дои:10.1145/1743546.1743567.
- Масуда, Сумио; Накадзима, Кадзуо; Кашивабара, Тошинобу; Fujisawa, Toshio (1990), "Минимизация пересечений в линейных вложениях графов", Транзакции IEEE на компьютерах, 39 (1): 124–127, Дои:10.1109/12.46286, МИСТЕР 1032144.
- Николсон, Т. А. Дж. (1968), "Процедура перестановки для минимизации количества пересечений в сети", Труды института инженеров-электриков, 115: 21–26, Дои:10.1049 / piee.1968.0004, МИСТЕР 0311416.
- Преториус, А. Дж .; ван Вейк, Дж. Дж. (2007), «Преодоление семантического разрыва: визуализация графов переходов с помощью пользовательских диаграмм», Компьютерная графика и приложения IEEE, 27 (5): 58–66, Дои:10.1109 / MCG.2007.121, PMID 17913025, S2CID 8643133.
- Саати, Томас Л. (1964), «Минимальное количество пересечений в полных графах», Труды Национальной академии наук Соединенных Штатов Америки, 52 (3): 688–690, Дои:10.1073 / pnas.52.3.688, МИСТЕР 0166772, ЧВК 300329, PMID 16591215.
- Ваттенберг, М. (2002), «Дуговые диаграммы: визуализация структуры в строках», Proc. Симпозиум IEEE по визуализации информации (INFOVIS 2002), стр. 110–116, Дои:10.1109 / INFVIS.2002.1173155, ISBN 0-7695-1751-X, S2CID 881989.