График облигаций - Bond graph

Простой масса – пружина – демпфер система, и ее эквивалентная форма графа связей

А граф облигаций это графическое представление физического динамическая система. Это позволяет преобразовать систему в представление в пространстве состояний. Это похоже на блок-схема или же график потока сигналов, с той основной разницей, что дуги в графах связей представляют двунаправленный обмен физическими энергия, в то время как на блок-схемах и графиках потока сигналов представлены однонаправленный Поток информации. Графики связи являются мультиэнергетическими (например, механическими, электрическими, гидравлическими и т. Д.) И нейтральными. Это означает, что граф связей может легко включать несколько доменов.

График связи состоит из «связей», которые связывают вместе элементы «однопортовый», «двухпортовый» и «многопортовый» (подробности см. Ниже). Каждая связь представляет собой мгновенный поток энергии (dE/dt) или же мощность. Поток в каждой облигации обозначается парой переменных, называемых степенными переменными, произведение которых представляет собой мгновенную мощность облигации. Переменные мощности разбиты на две части: расход и усилие. Например, для соединения электрической системы поток - это ток, а усилие - это напряжение. Умножив ток и напряжение в этом примере, вы можете получить мгновенную мощность связи.

У облигации есть еще две особенности, которые кратко описаны здесь и более подробно описаны ниже. Один из них - условное обозначение «полустрелки». Это определяет предполагаемое направление потока положительной энергии. Как и в случае схем электрических цепей и диаграмм свободного тела, выбор положительного направления является произвольным, с оговоркой, что аналитик должен во всем согласовываться с выбранным определением. Другая особенность - «причинность». Это вертикальная полоса, размещенная только на одном конце связи. Это не произвольно. Как описано ниже, существуют правила для назначения надлежащей причинности данному порту и правила для приоритета между портами. Причинность объясняет математическую связь между усилием и потоком. Положения причинно-следственных связей показывают, какие из переменных мощности являются зависимыми, а какие независимыми.

Если динамика моделируемой физической системы работает в широком диапазоне масштабов времени, быстрое непрерывное поведение может быть смоделировано как мгновенное явление с помощью граф гибридной связи. Графики облигаций были изобретены Генри Пэйнтер.^[1]

Тетраэдр состояния

Тетраэдр состояния

Тетраэдр состояния - это тетраэдр, который графически показывает преобразование между усилием и потоком. На соседнем изображении показан тетраэдр в обобщенном виде. Тетраэдр можно модифицировать в зависимости от области энергий. В таблице ниже показаны переменные и константы тетраэдра состояния в общих областях энергии.

Энергетический домен[2][Примечание 1]		${displaystyle f (t)}$	${displaystyle e (t)}$	${displaystyle q (t)}$	${displaystyle p (t)}$	${displaystyle R}$	${displaystyle I}$	${displaystyle C}$
Обобщенный	Имя	Обобщенный поток	Общее усилие	Обобщенное перемещение	Обобщенный импульс	Сопротивление	Инертность	Согласие
	Символ	${displaystyle f (t)}$	${displaystyle e (t)}$	${displaystyle q (t)}$	${displaystyle p (t)}$	${displaystyle R}$	${displaystyle I}$	${displaystyle C}$
Линейный механический	Имя	Скорость	Сила	Смещение	Линейный импульс	Постоянная демпфирования	Масса	Обратная величина жесткости пружины
	Символ	${displaystyle v (t)}$	${displaystyle F (t)}$	${displaystyle x (t)}$	${displaystyle p (t)}$	${displaystyle b}$	${displaystyle m}$	${displaystyle {frac {1} {k}}}$
	Единицы	${displaystyle m / s}$	${displaystyle N}$	${displaystyle m}$	${displaystyle Ncdot s}$	${displaystyle Ncdot s / m}$	${displaystyle кг}$	${displaystyle m / N}$
Угловой механический	Имя	Угловая скорость	Крутящий момент	Угловое смещение	Угловой момент	Угловое демпфирование	Момент инерции массы	Инверсия угловой жесткости пружины
	Символ	${displaystyle omega (t)}$	${displaystyle T (t)}$	${displaystyle heta (t)}$	${displaystyle p_ {au} (t)}$	${displaystyle B}$	${displaystyle J}$	${displaystyle {frac {1} {k_ {au}}}}$
	Единицы	${displaystyle rad / s}$	${displaystyle Ncdot m}$	${displaystyle rad}$	${displaystyle Ncdot mcdot s}$	${displaystyle rad / (Ncdot mcdot s)}$	${displaystyle kgcdot m ^ {2}}$	${displaystyle 1 / (Ncdot m)}$
Электромагнитный	Имя	Текущий	Напряжение	Обвинять	Потоковая связь	Сопротивление	Индуктивность	Емкость
	Символ	${displaystyle i (t)}$	${displaystyle V (t)}$	${displaystyle q (t)}$	${displaystyle lambda (t)}$	${displaystyle R}$	${displaystyle L}$	${displaystyle C}$
	Единицы	${displaystyle A}$	${displaystyle V}$	${displaystyle C}$	${displaystyle Vcdot s}$	${displaystyle Omega}$	${displaystyle H}$	${displaystyle F}$
Гидравлический/ пневматический	Имя	Объемный расход	Давление	Объем	Жидкий импульс	Сопротивление жидкости	Индуктивность жидкости	Место хранения
	Символ	${displaystyle varphi (t)}$	${displaystyle P (t)}$	${displaystyle V (t)}$	${displaystyle p_ {f} (t)}$	${displaystyle R_ {f}}$	${displaystyle I_ {f}}$	${displaystyle C_ {f}}$
	Единицы	${displaystyle m ^ {3} / s}$	${displaystyle Pa}$	${displaystyle m ^ {3}}$	${displaystyle Pacdot s}$	${displaystyle Pacdot s / m ^ {3}}$	${displaystyle Pacdot s ^ {2} / m ^ {3}}$	${displaystyle m ^ {3} / Па}$

Используя тетраэдр состояния, можно найти математическую связь между любыми переменными на тетраэдре. Это делается путем следования стрелкам вокруг диаграммы и умножения любых констант по пути. Например, если вы хотите найти связь между обобщенным потоком и обобщенным перемещением, вы должны начать с f (t) а затем интегрировать его, чтобы получить q (t). Больше примеров уравнений можно увидеть ниже.

Связь между обобщенным перемещением и обобщенным потоком.

${displaystyle q (t) = int f (t) имя оператора {d}! t}$

Связь между обобщенным потоком и обобщенным усилием.

${displaystyle f (t) = {frac {1} {R}} cdot e (t)}$

Связь между обобщенным потоком и обобщенным импульсом.

${displaystyle f (t) = {frac {1} {I}} cdot p (t)}$

Связь между обобщенным импульсом и обобщенным усилием.

${displaystyle p (t) = int e (t) имя оператора {d}! t}$

Связь между обобщенным потоком и обобщенным усилием, включающая постоянную C.

${displaystyle e (t) = {frac {1} {C}} int f (t) имя оператора {d}! t}$

Все математические соотношения остаются неизменными при переключении энергетических областей, меняются только символы. Это можно увидеть на следующих примерах.

Связь между смещением и скоростью.

${displaystyle x (t) = int v (t) имя оператора {d}! t}$

Связь между током и напряжением, также известная как Закон Ома.

${displaystyle i (t) = {frac {1} {R}} cdot V (t)}$

Связь между силой и перемещением, также известная как Закон Гука. Отрицательный знак опускается в этом уравнении, потому что знак учитывается в направлении стрелки на графике облигаций.

${displaystyle F (t) = kcdot x (t)}$

Составные части

Если двигатель соединен с колесом через вал, мощность передается во вращательной механической области, что означает, что усилие и поток представляют собой крутящий момент (τ) и угловую скорость (ω) соответственно. Граф связи слов - это первый шаг к графу связи, в котором слова определяют компоненты. В виде графа словесных облигаций эта система могла бы выглядеть так:

${displaystyle {ext {engine}}; {overset {extstyle au} {underset {extstyle omega} {- !!! - !!! - !!! - !!! -}}}; {ext {wheel}}}$

Полустрелка используется для обозначения знака, поэтому, если двигатель работает, когда τ и ω положительны, тогда будет нарисована диаграмма:

${displaystyle {ext {engine}}; {overset {extstyle au} {underset {extstyle omega} {- !!! - !!! - !!! ightharpoondown}}}; {ext {wheel}}}$

Эта система также может быть представлена ​​в более общем виде. Это предполагает переход от использования слов к символам, представляющим одни и те же предметы. Эти символы основаны на обобщенной форме, как объяснено выше. Поскольку двигатель передает крутящий момент на колесо, он будет представлен как источник усилия для системы. Колесо может быть представлено импедансом в системе. Далее символы крутящего момента и угловой скорости опускаются и заменяются обобщенными символами усилия и потока. Хотя в этом примере это не обязательно, связи обычно нумеруют, чтобы отслеживать их в уравнениях. Упрощенную схему можно увидеть ниже.

${displaystyle {S_ {e}}; {overset {extstyle e_ {1}} {underset {extstyle f_ {1}} {- !!! - !!! - !!! ightharpoondown}}}; {ext {I} }}$

Учитывая, что усилие всегда превышает поток по связке, также можно полностью отказаться от символов усилия и потока без потери какой-либо соответствующей информации. Однако не следует опускать номер облигации. Пример можно увидеть ниже.

${displaystyle {S_ {e}}; {overset {extstyle _ {1}} {underset {extstyle} {- !!! - !!! - !!! ightharpoondown}}}; {ext {I}}}$

Номер связи будет важен позже при преобразовании графа связей в уравнения пространства состояний.

Однопортовые элементы

Элементы с одним портом - это элементы в графе связей, которые могут иметь только один порт.

Источники и стоки

Источники - это элементы, которые представляют вход для системы. Они будут либо вкладывать усилия, либо перетекать в систему. Они обозначаются заглавной буквой «S» и строчной буквой «е» или «f» для обозначения усилия или расхода соответственно. У источников всегда будет стрелка, указывающая от элемента. Примеры источников: двигатели (источник усилия, крутящего момента), источники напряжения (источник усилия) и источники тока (источник потока).

${displaystyle S_ {e}; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! ightharpoonup !!!}}}; Jqquad {ext {и}} qquad S_ {f}; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! ightharpoonup !!!}}}; J}$

куда J указывает соединение.

Раковины - это элементы, которые представляют выход для системы. Они представлены так же, как и источники, но имеют стрелку, указывающую на элемент, а не от него.

${displaystyle J; {overset {extstyle} {underset {extstyle} {leftharpoonup !!! - !!! - !!! - !!! - !!!}}}; S_ {e} qquad {ext {and}} qquad J; {overset {extstyle} {underset {extstyle} {leftharpoonup !!! - !!! - !!! - !!!}}}; S_ {f}}$

Инерция

Элементы инерции обозначаются большой буквой «I», и в них всегда течет энергия. Инерционные элементы - это элементы, накапливающие энергию. Чаще всего это масса для механических систем и индукторы для электрических систем.

${displaystyle J; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! ightharpoonup !!!}}}; Я}$

Сопротивление

Элементы сопротивления обозначены заглавной буквой «R», и в них всегда течет сила. Элементы сопротивления - это элементы, рассеивающие энергию. Чаще всего это демпфер для механических систем и резисторы для электрических систем.

${displaystyle J; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! ightharpoonup !!!}}}; Р}$

Согласие

Элементы соответствия обозначены заглавной буквой «С», и в них всегда втекает сила. Элементы соответствия - это элементы, которые хранят потенциальную энергию. Чаще всего это пружины для механических систем и конденсаторы для электрических систем.

${displaystyle J; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! ightharpoonup !!!}}}; C}$

Двухпортовые элементы

Эти элементы имеют два порта. Они используются для изменения мощности между системой или внутри нее. При преобразовании из одного в другой во время передачи не теряется мощность. У элементов есть константа, которая будет дана вместе с ней. Константа называется постоянной трансформатора или постоянной гиратора в зависимости от того, какой элемент используется. Эти константы обычно отображаются в виде отношения под элементом.

Трансформатор

Трансформатор применяет соотношение между потоком в потоке и усилием в выходе. Примеры включают идеальный электрический трансформатор или рычаг.

Обозначается

${displaystyle {egin {matrix} {overset {extstyle _ {1}} {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} TR {overset {extstyle _ {2} } {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} ^ {r: 1} end {matrix}}}$

где р обозначает модуль трансформатора. Это означает

${displaystyle f_ {1} cdot r = f_ {2}}$

и

${displaystyle e_ {2} cdot r = e_ {1}}$

Гиратор

А гиратор применяет взаимосвязь между потоком в выходящем усилии и выходящим усилием. Примером гиратора является двигатель постоянного тока, который преобразует напряжение (электрическое усилие) в угловую скорость (угловой механический поток).

${displaystyle {egin {matrix} {overset {extstyle _ {1}} {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} GY {overset {extstyle _ {2} } {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} ^ {g: 1} end {matrix}}}$

означающий, что

${displaystyle e_ {2} = gcdot f_ {1},}$

и

${displaystyle e_ {1} = gcdot f_ {2}.,}$

Многопортовые элементы

Соединения, в отличие от других элементов, могут иметь любое количество входных или выходных портов. Соединения распределяют мощность между своими портами. Есть два различных соединения, 0-соединение и 1-соединение, которые различаются только тем, как усилие и поток переносятся. Один и тот же переход в серии можно комбинировать, но нельзя использовать разные соединения в серии.

0-переходы

0-соединения ведут себя так, что все значения усилий равны между связями, но сумма значений расхода в равной сумме значений расхода на выходе, или, что эквивалентно, сумма всех потоков равна нулю. В электрической цепи 0-переход является узлом и представляет собой напряжение, разделяемое всеми компонентами в этом узле. В механической схеме 0-соединение представляет собой соединение между компонентами и представляет собой силу, разделяемую всеми компонентами, подключенными к нему.

${displaystyle все е равны}$

${displaystyle sum f_ {in} = sum f_ {out}}$

Пример показан ниже.

${displaystyle {overset {extstyle _ {1}} {underset {extstyle} {- !!! - !!! - !!! ightharpoondown}}} {stackrel {extstyle {stackrel {extstyle _ {2}} {upharpoonright}} } {0}} {overset {extstyle _ {3}} {underset {extstyle} {- !!! - !!! - !!! ightharpoondown}}}}$

Результирующие уравнения:

${displaystyle e_ {1} = e_ {2} = e_ {3}}$

${displaystyle f_ {1} = f_ {2} + f_ {3}}$

1-переходы

1-переходы ведут себя противоположно 0-переходам. 1-переходы ведут себя так, что все значения потока равны по всем связям, но сумма значений усилий равна сумме значений усилий на выходе, или, что эквивалентно, сумма всех усилий равна нулю. В электрической цепи 1 переход представляет собой последовательное соединение компонентов. В механической схеме 1-переход представляет собой скорость, разделяемую всеми подключенными к нему компонентами.

${displaystyle все f равны}$

${displaystyle sum e_ {in} = sum e_ {out}}$

Пример показан ниже.

${displaystyle {overset {extstyle _ {1}} {underset {extstyle} {- !!! - !!! - !!! ightharpoondown}}} {stackrel {extstyle {stackrel {extstyle _ {2}} {upharpoonright}} } {1}} {overset {extstyle _ {3}} {underset {extstyle} {- !!! - !!! - !!! ightharpoondown}}}}$

Результирующие уравнения:

${displaystyle f_ {1} = f_ {2} = f_ {3}}$

${displaystyle e_ {1} = e_ {2} + e_ {3}}$

Причинно-следственная связь

Графики связи имеют понятие причинности, указывающее, какая сторона связи определяет мгновенное усилие, а какая - мгновенный поток. При формулировании динамических уравнений, описывающих систему, причинно-следственная связь определяет для каждого элемента моделирования, какая переменная является зависимой, а какая независимой. Графическое распространение причинно-следственной связи от одного элемента моделирования к другому упрощает анализ крупномасштабных моделей. Завершение причинно-следственных связей в модели графа связей позволит обнаружить ситуацию моделирования, в которой существует алгебраический цикл; это ситуация, когда переменная определяется рекурсивно как функция самой себя.

В качестве примера причинно-следственной связи рассмотрим конденсатор, включенный последовательно с батареей. Физически невозможно зарядить конденсатор мгновенно, поэтому все, что подключено параллельно конденсатору, обязательно будет иметь то же напряжение (переменная усилия), что и на конденсаторе. Точно так же индуктор не может мгновенно изменять поток, поэтому любой компонент, включенный последовательно с индуктором, обязательно будет иметь тот же поток, что и индуктор. Поскольку конденсаторы и катушки индуктивности являются пассивными устройствами, они не могут поддерживать свое соответствующее напряжение и течь бесконечно - компоненты, к которым они присоединены, будут влиять на их соответствующее напряжение и поток, но только косвенно, влияя на их ток и напряжение соответственно.

Примечание: причинно-следственная связь - это симметричная связь. Когда одна сторона «вызывает» усилие, другая «вызывает» поток.

В обозначении графа связей причинный штрих может быть добавлен к одному концу силового соединения, чтобы указать, что противоположный конец определяет усилие. Рассмотрим двигатель с постоянным крутящим моментом, приводящий в движение колесо, то есть источник усилия (SE). Это будет выглядеть следующим образом:

${displaystyle {egin {array} {r} {ext {motor}} SEend {array}}; {overset {extstyle au} {underset {extstyle omega} {- !!! - !!! - !!! ightharpoonup! !! |}}}; {ext {wheel}}}$

Симметрично сторона с причинным штрихом (в данном случае колесо) определяет поток для связки.

Причинная связь приводит к ограничениям совместимости. Очевидно, что только один конец связи власти может определять усилие, и поэтому только один конец связи может иметь причинный удар. Кроме того, два пассивных компонента с поведением, зависящим от времени, я и C, может иметь только один вид причинности: я компонент определяет поток; а C компонент определяет усилие. Итак, с перекрестка, J, предпочтительная причинно-следственная ориентация следующая:

${displaystyle J; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! ightharpoonup !!! |}}}; Iqquad {ext {and}} qquad J; {overset {extstyle } {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}}; C}$

Причина, по которой это предпочтительный метод для этих элементов, может быть дополнительно проанализирована, если вы рассмотрите уравнения, которые они давали бы, показанные тетраэдром состояния.

${displaystyle f (t) = {frac {1} {I}} int e (t) имя оператора {d}! tqquad {ext {and}} qquad e (t) = {frac {1} {C}} int f (t) имя оператора {d}! t}$

Полученные уравнения включают интеграл от независимой степенной переменной. Это предпочтительнее, чем результат наличия другой причинной связи, которая приводит к производной. Уравнения можно увидеть ниже.

${displaystyle e (t) = Icdot {точка {f}} (t) qquad {ext {and}} qquad f (t) = Ccdot {точка {e}} (t)}$

График облигаций может иметь причинную полосу на одном из этих элементов нежелательным образом. В таком случае говорят, что в этой связи произошел «причинный конфликт». Результаты причинного конфликта видны только при написании пространство состояний уравнения для графика. Более подробно это объясняется в этом разделе.

У резистора нет зависящего от времени поведения: приложите напряжение и получите поток мгновенно, или примените поток и получите напряжение мгновенно, таким образом, резистор может быть на любом конце причинной связи:

${displaystyle J; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! ightharpoonup !!! |}}}; Rqquad {ext {and}} qquad J; {overset {extstyle } {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}}; R}$

Источники потока (SF) определить поток, источники усилий (SE) определить усилие. Трансформаторы пассивны, не рассеивают и не накапливают энергию, поэтому причинно-следственная связь проходит через них:

${displaystyle; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! - !!! -! |}}}; TF; {overset {extstyle} {underset {extstyle} { - !!! - !!! - !!! - !!! -! |}}}; qquad {ext {or}} qquad; {overset {extstyle} {underset {extstyle} {| !!! - !! ! - !!! - !!! - !!! -}}}; TF; {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! - !! ! -}}};}$

Гиратор преобразует поток в усилие и усилие в потоке, поэтому, если поток создается с одной стороны, усилие создается с другой стороны, и наоборот:

${displaystyle; {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! - !!! -}}}; GY; {overset {extstyle} {underset {extstyle} } {- !!! - !!! - !!! - !!! -! |}}}; qquad {ext {or}} qquad; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! - !!! -! |}}}; GY; {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! - !! ! -}}};}$

Узлы

В 0-разветвлении усилия равны; в 1-узле потоки равны. Таким образом, в случае причинно-следственных связей только одна связь может вызвать усилие в 0-соединении, и только одна может вызвать поток в 1-соединении. Таким образом, если известна причинность одной связи стыка, известна также причинность других. Эта одна облигация называется "сильной связью".

${displaystyle {ext {strong bond}} ightarrow; dashv! {overset {extstyle op} {underset {extstyle ot} {0}}}! dashv qquad {ext {and}} qquad {ext {strong bond}} ightarrow; vdash ! {overset {extstyle ot} {underset {extstyle op} {1}}}! vdash}$

Определение причинно-следственной связи

Чтобы определить причинно-следственную связь графа облигаций, необходимо выполнить определенные шаги. Вот эти шаги:

1. Нарисуйте причинные столбики источника
2. Изобразите предпочтительную причинно-следственную связь для связей C и I
3. Нарисуйте причинные стержни для 0 и 1 соединений, трансформаторов и гираторов.
4. Нарисуйте столбики причинно-следственных связей R
5. Если возникает причинный конфликт, измените связь C или I на дифференциацию.

Шаги по шагам показаны ниже.

${displaystyle {egin {matrix} S_ {f} & {overset {extstyle} {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} & 0 & {overset {extstyle} {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} & TR & {overset {extstyle} {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} & 0 & {overset {extstyle} {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} & C_ {5} && downharpoonleft && ^ {r: 1} && downharpoonleft && && C_ {2} &&&& R_ {6} && end {matrix}}}$

Первый шаг - это выявить причинно-следственную связь для источников, но она только одна. Это дает график ниже.

${displaystyle {egin {matrix} S_ {f} & {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} & 0 & {overset {extstyle} { underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} & TR & {overset {extstyle} {underset {extstyle} {!!! - !!! - !!! - !! ! ightharpoonup}}} & 0 & {overset {extstyle} {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} & C_ {5} && downharpoonleft && ^ {r: 1} && downharpoonleft && && C_ {2} &&&& R_ {6} && end {matrix}}}$

Следующим шагом является построение предпочтительной причинно-следственной связи для связей C.

${displaystyle {egin {matrix} S_ {f} & {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} & 0 & {overset {extstyle} { underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} & TR & {overset {extstyle} {underset {extstyle} {!!! - !!! - !!! - !! ! ightharpoonup}}} & 0 & {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} & C_ {5} && {ar {downharpoonleft}} && ^ {r: 1} && downharpoonleft && && C_ {2} &&&& R_ {6} && end {matrix}}}$

Затем примените причинность для переходов 0 и 1, трансформаторов и гираторов.

${displaystyle {egin {matrix} S_ {f} & {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} & 0 & {overset {extstyle} { underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} & TR & {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} & 0 & {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} & C_ {5} && {ar {downharpoonleft} } && ^ {r: 1} && {underline {downharpoonleft}} && && C_ {2} &&&& R_ {6} && end {matrix}}}$

Однако есть проблема с 0-образным переходом слева. Нулевое соединение имеет две причинные полосы на соединении, но нулевое соединение требует одного и только одного на соединении. Это было вызвано наличием ${extstyle C_ {2}}$ быть в предпочтительной причинности. Единственный способ исправить это - перевернуть шкалу причинно-следственных связей. Это приводит к причинному конфликту, исправленная версия графика ниже, с ${extstyle star}$ представляющий причинный конфликт.

${displaystyle {egin {matrix} S_ {f} & {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} & 0 & {overset {extstyle} { underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} & TR & {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} & 0 & {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} & C_ {5} && {underline {downharpoonleft} } звезда && ^ {r: 1} && {underline {downharpoonleft}} && && C_ {2} &&&& R_ {6} && end {matrix}}}$

Конвертация из других систем

Одно из основных преимуществ использования графов связей состоит в том, что если у вас есть граф связей, исходная энергетическая область не имеет значения. Ниже приведены некоторые шаги, которые необходимо выполнить при преобразовании из энергетической области в граф связей.

Электромагнитный

Шаги для решения электромагнитной проблемы в виде графа связи следующие:

1. Поместите нулевое соединение в каждый узел
2. Вставьте источники, связи R, I, C, TR и GY с 1 переходом
3. Земля (с обеих сторон, если присутствует трансформатор или гиратор)
4. Назначьте направление потока мощности
5. Упрощать

Эти шаги более четко показаны в примерах ниже.

Линейно-механический

Шаги для решения линейной механической задачи в виде графа связей следующие:

1. Поместите 1-переходы для каждой отдельной скорости (обычно при массе)
2. Вставьте связи R и C в их собственные 0-соединения между соединениями 1, где они действуют
3. Вставьте источники и связи I на стыках 1, где они действуют
4. Назначьте направление потока мощности
5. Упрощать

Эти шаги более четко показаны в примерах ниже.

Упрощение

Этап упрощения одинаков независимо от того, была ли система электромагнитной или линейно-механической. Шаги следующие:

1. Удалить связь нулевой мощности (из-за земли или нулевой скорости)
2. Удалите соединения 0 и 1 с менее чем тремя связями
3. Упростите параллельное питание
4. Объединить 0 стыков последовательно
5. Объедините 1 соединение последовательно

Эти шаги более четко показаны в примерах ниже.

Параллельная мощность

Параллельное питание - это когда питание работает параллельно в графе связи. Пример параллельного питания показан ниже.

Параллельное питание можно упростить, вспомнив взаимосвязь между усилием и потоком для 0- и 1-переходов. Чтобы решить параллельную мощность, вам сначала нужно записать все уравнения для соединений. Для представленного примера уравнения можно увидеть ниже. (Обратите внимание на число, которое представляет переменная усилие / расход).

${displaystyle {egin {matrix} f_ {1} = f_ {2} = f_ {3} && e_ {2} = e_ {4} = e_ {7} e_ {1} = e_ {2} + e_ {3} && f_ {2} = f_ {4} + f_ {7} && e_ {3} = e_ {5} = e_ {6} && f_ {7} = f_ {6} = f_ {8} f_ {3} = f_ {5} + f_ {6} && e_ {7} + e_ {6} = e_ {8} end {matrix}}}$

Манипулируя этими уравнениями, вы можете расположить их так, чтобы вы могли найти эквивалентный набор 0 и 1-переходов для описания параллельной мощности.

Например, потому что ${extstyle e_ {3} = e_ {6}}$ и ${extstyle e_ {2} = e_ {7}}$ вы можете заменить переменные в уравнении ${extstyle e_ {1} = e_ {2} + e_ {3}}$ в результате чего ${extstyle e_ {1} = e_ {6} + e_ {7}}$ и с тех пор

${extstyle e_ {6} + e_ {7} = e_ {8}}$, теперь мы знаем, что ${displaystyle e_ {1} = e_ {8}}$. Это соотношение уравнивания двух переменных усилия можно объяснить нулевым переходом. Управляя другими уравнениями, вы можете обнаружить, что ${displaystyle f_ {4} = f_ {5}}$ который описывает отношения 1-перехода. После того, как вы определили нужные вам взаимосвязи, вы можете перерисовать параллельную силовую часть с новыми соединениями. Результат для примера показан ниже.

Примеры

Простая электрическая система

Простая электрическая цепь, состоящая из последовательно соединенных источника напряжения, резистора и конденсатора.

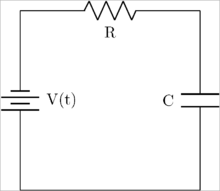
Первый шаг - нарисовать 0-образные соединения на всех узлах. Результат показан ниже.

${displaystyle {egin {matrix} & 0 && 0 & &&&& &&&& & 0 && 0 & end {matrix}}}$

Следующим шагом будет добавление всех элементов, действующих на их собственном 1-соединении. Результат ниже.

${displaystyle {egin {matrix} &&&& R &&&& &&&& | &&&& && 0 & - & 1 & - & 0 && && | &&&& | && S_ {e} & - & 1 &&&& 1 & - & C && | &&&& | && && {underline {0}} & - & - & - & 0 && конец {матрица}}}$

Следующий шаг - выбрать почву. Заземление - это просто 0-переходный переход, который, как предполагается, не имеет напряжения. В этом случае земля будет выбрана как нижний левый 0-образный перекресток, подчеркнутый выше. Следующий шаг - нарисовать все стрелки для графика облигаций. Стрелки на соединениях должны указывать на землю (по тому же пути, что и ток). Для элементов сопротивления, инертности и податливости стрелки всегда указывают на элементы. Результат рисования стрелок можно увидеть ниже, где 0-образный перекресток отмечен звездой в качестве земли.

Теперь, когда у нас есть график Бонда, мы можем начать процесс его упрощения. Первый шаг - удалить все наземные узлы. Оба нижних 0-переходника можно удалить, потому что они оба заземлены. Результат показан ниже.

Затем можно удалить соединения с менее чем тремя связями. Это связано с тем, что поток и усилие проходят через эти соединения без изменений, поэтому их можно удалить, чтобы мы могли рисовать меньше. Результат можно увидеть ниже.

Последний шаг - применить причинно-следственную связь к графу облигаций. Применение причинности объяснялось выше. Окончательный график облигаций показан ниже.

Продвинутая электрическая система

Более совершенная электрическая система с источником тока, резисторами, конденсаторами и трансформатором.

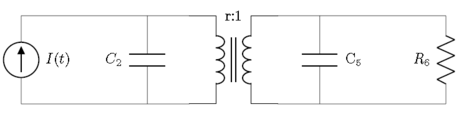
Выполнение шагов с этой схемой приведет к приведенному ниже графику связей, прежде чем он будет упрощен. Узлы, отмеченные звездочкой, обозначают землю.

Упрощение графа облигаций приведет к изображению ниже.

Наконец, применение причинно-следственной связи приведет к приведенному ниже графику облигаций. Связь со звездой обозначает причинный конфликт.

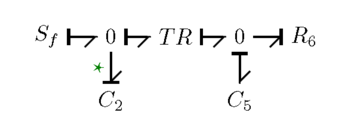
Простая линейная механика

Простая линейная механическая система, состоящая из массы на пружине, прикрепленной к стене. К массе приложена некоторая сила. Изображение системы показано ниже.

Для механической системы первый шаг состоит в том, чтобы разместить 1-узел на каждой отдельной скорости, в этом случае есть две различные скорости, масса и стенка. Обычно полезно пометить 1-переходы для справки. Результат ниже.

${displaystyle {egin {matrix} && && 1_ {mass} && && && && 1_ {wall} && end {matrix}}}$

Следующий шаг - нарисовать связи R и C в их собственных 0-переходах между 1-переходами, где они действуют. В этом примере есть только одна из этих связей, связь C для пружины. Он действует между 1-соединением, представляющим массу, и 1-соединением, представляющим стену. Результат ниже.

${displaystyle {egin {matrix} && && 1_ {mass} && | && 0 & - & C: {frac {1} {k}} | && 1_ {wall} && end {matrix}}}$

Затем вы хотите добавить источники и связи на 1-переходе, где они действуют. Есть один источник, источник усилия (силы) и одна связь I, масса массы, оба из которых действуют на 1-стык массы. Результат показан ниже.

${displaystyle {egin {matrix} S_ {e}: F (t) && | && 1_ {mass} & - & I: m | && 0 & - & C: {frac {1} {k}} | && 1_ {стена} && конец {матрица}}}$

Далее вы хотите назначить поток мощности. Как и в электрических примерах, мощность должна течь по направлению к земле, в данном случае к 1-му стыку стены. Исключениями являются облигации R, C или I, которые всегда указывают на элемент. Полученный график облигаций представлен ниже.

Теперь, когда граф облигаций создан, его можно упростить. Поскольку стена заземлена (имеет нулевую скорость), вы можете удалить это соединение. Таким образом, 0-соединение, на котором находится связь C, также может быть удалено, потому что тогда в нем будет меньше трех связей. Упрощенный график облигаций можно увидеть ниже.

Последний шаг - применить причинно-следственную связь, окончательный график связи можно увидеть ниже.

Продвинутая линейная механика

Ниже представлена ​​более совершенная линейная механическая система.

Как и в приведенном выше примере, первым шагом является создание 1-переходов на каждой удаленной скорости. В этом примере есть три удаленных скорости: Масса 1, Масса 2 и стена. Затем вы подключаете все связи и назначаете поток энергии. Облигацию можно увидеть ниже.

Затем вы начинаете процесс упрощения графа связей, удаляя 1-стык стены и удаляя стыки с менее чем тремя связями. График облигаций можно увидеть ниже.

На графике облигаций присутствует параллельная мощность. Решение проблемы параллельной мощности было объяснено выше. Результат ее решения можно увидеть ниже.

Наконец, примените причинно-следственную связь, окончательный график связи можно увидеть ниже.

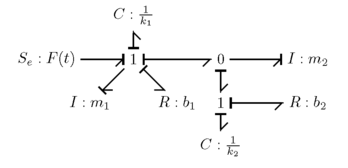
Уравнения состояния

После завершения графа облигаций его можно использовать для создания представление в пространстве состояний уравнения системы. Представление в пространстве состояний особенно мощно, поскольку оно позволяет выполнять сложные многоуровневые дифференциал Вместо этого система должна решаться как система уравнений первого порядка. Общий вид уравнения состояния можно увидеть ниже.

${displaystyle {точка {extbf {x}}} (t) = {extbf {A}} cdot {extbf {x}} (t) + {extbf {B}} cdot {extbf {u}} (t)}$

Где, ${extstyle {extbf {x}} (т)}$ матрица-столбец переменные состояния, или неизвестные системы. ${extstyle {точка {extbf {x}}} (т)}$ это производная по времени переменных состояния. ${extstyle {extbf {u}} (т)}$матрица-столбец входов системы. И ${extstyle {extbf {A}}}$ и ${extstyle {extbf {B}}}$ - матрицы констант, основанные на системе. Переменные состояния системы: ${extstyle q (t)}$ и ${extstyle p (t)}$ значения для каждой связи C и I без причинного конфликта. Каждый я облигации получает ${extstyle p (t)}$ в то время как каждая облигация C получает ${extstyle q (t)}$.

Например, если у вас есть график облигаций, показанный ниже.

Были бы следующие ${extstyle {точка {extbf {x}}} (т)}$, ${extstyle {extbf {x}} (т)}$, и ${extstyle {extbf {u}} (т)}$ матрицы.

${displaystyle {dot {extbf {x}}} (t) = left [{egin {matrix} {dot {p}} _ {3} (t) {dot {q}} _ {6} (t) end) {matrix}} ight] qquad {ext {and}} qquad {extbf {x}} (t) = left [{egin {matrix} p_ {3} (t) q_ {6} (t) end {matrix}). } ight] qquad {ext {и}} qquad {extbf {u}} (t) = left [{egin {matrix} e_ {1} (t) end {matrix}} ight]}$

Матрицы ${extstyle {extbf {A}}}$ и ${extstyle {extbf {B}}}$ решаются путем определения взаимосвязи переменных состояния и их соответствующих элементов, как было описано в тетраэдре состояния. Первый шаг к решению уравнений состояния - составить список всех определяющих уравнений для графа связей. В таблице ниже показана взаимосвязь между связями и их определяющими уравнениями.

	Название облигации	Связь с Причинно-следственная связь	Управляющее уравнение (я)
«♦» обозначает предпочтительную причинно-следственную связь
Один порт Элементы	Источник / Приемник, S	${displaystyle S_ {e}; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! ightharpoonup !!! |}}};}$	${displaystyle input = e (t)}$
		${displaystyle S_ {f}; {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}};}$	${displaystyle input = f (t)}$
	Сопротивление, R: Рассеянная энергия	${displaystyle; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! ightharpoonup !!! |}}} R}$	${displaystyle f (t) = {frac {1} {R}} cdot e (t)}$
		${displaystyle; {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} R}$	${displaystyle e (t) = Rcdot f (t)}$
	Инертность, I: Кинетическая энергия	♦${displaystyle; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! ightharpoonup !!! |}}} I}$	${displaystyle f (t) = {frac {1} {I}} int e (t) имя оператора {d}! t}$
		${displaystyle; {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} I}$	${displaystyle e (t) = Icdot {точка {f}} (t)}$
	Соответствие, C: Потенциальная энергия	${displaystyle; {overset {extstyle} {underset {extstyle} {- !!! - !!! - !!! ightharpoonup !!! |}}} C}$	${displaystyle f (t) = Ccdot {точка {e}} (t)}$
		♦${displaystyle; {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} C}$	${displaystyle e (t) = {frac {1} {C}} int f (t) имя оператора {d}! t}$
Два порта Элементы	Трансформатор, TR	${displaystyle {egin {matrix} {overset {extstyle} {{underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}} |}} TR {overset {extstyle} {underset {extstyle} } {!!! - !!! - !!! - !!! ightharpoonup}}} | ^ {r: 1} конец {матрица}}}$	${displaystyle f_ {1} r = f_ {2}}$ ${displaystyle e_ {2} r = e_ {1}}$
		${displaystyle {egin {matrix} | {overset {extstyle} {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} TR | {overset {extstyle} {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} ^ {r: 1} end {matrix}}}$
	Гиратор, GY	${displaystyle {egin {matrix} | {overset {extstyle} {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} GY {overset {extstyle} {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} | ^ {g: 1} конец {матрица}}}$	${displaystyle f_ {1} g = e_ {2}}$ ${displaystyle f_ {2} g = e_ {1}}$
		${displaystyle {egin {matrix} {overset {extstyle} {underset {extstyle} {!!! - !!! - !!! - !!! ightharpoonup}}} | GY {overset {extstyle} {underset {extstyle} {| !!! - !!! - !!! - !!! ightharpoonup}}} ^ {g: 1} end {matrix}}}$
Многопортовый Элементы	0 перекресток	Один и только один причинная полоса на стыке	${displaystyle all e (t) =}$
			${displaystyle sum f (t) _ {in} = sum f (t) _ {out}}$
	1 перекресток	одна и только одна причина бар подальше от перекрестка	${displaystyle sum e (t) _ {in} = sum e (t) _ {out}}$
			${displaystyle all f (t) =}$

В приведенном примере

Основные уравнения следующие.

${displaystyle {egin {matrix} input = e_ {1} & eq.1 e_ {1} = e_ {2} + e_ {3} + e_ {4} & eq.2 f_ {1} = f_ {2} = f_ {3} = f_ {4} & eq.3 e_ {2} = R_ {2} cdot f_ {2} & eq.4 f_ {3} = {frac {1} {I_ {3}}} int e_ {3} имя оператора {d}! T = {frac {1} {I_ {3}}} cdot p_ {3} & eq.5 f_ {4} cdot r = f_ {5} & eq.6 e_ {5} cdot r = e_ {4} & eq.7 e_ {5} = e_ {6} = e_ {7} & eq.8 f_ {5} = f_ {6} + f_ {7} & eq.9 e_ {6 } = {frac {1} {C_ {5}}} int f_ {6} имя оператора {d}! t = {frac {1} {C_ {6}}} cdot q_ {6} & eq.10 f_ {7 } = {frac {1} {R_ {7}}} cdot e_ {7} & eq.11end {matrix}}}$

Этими уравнениями можно манипулировать, чтобы получить уравнения состояния. В этом примере вы пытаетесь найти уравнения, которые связаны ${extstyle {точка {p}} _ {3} (t)}$ и ${extstyle {точка {q}} _ {6} (t)}$ с точки зрения ${extstyle p_ {3} (t)}$, ${extstyle q_ {6} (t)}$, и ${extstyle e_ {1} (t)}$.

Для начала следует вспомнить из тетраэдра состояния, что ${extstyle {точка {p}} _ {3} (t) = e_ {3} (t)}$начиная с уравнения 2, вы можете изменить его так, чтобы ${displaystyle e_ {3} = e_ {1} -e_ {2} -e_ {4}}$. ${displaystyle e_ {2}}$ можно заменить на уравнение 4, а в уравнении 4 ${displaystyle f_ {2}}$ можно заменить на ${displaystyle f_ {3}}$из-за уравнения 3, которое затем можно заменить уравнением 5. ${displaystyle e_ {4}}$ аналогичным образом можно заменить уравнением 7, в котором ${displaystyle e_ {5}}$можно заменить на ${displaystyle e_ {6}}$ которое затем можно заменить уравнением 10. После этой замены получается первое уравнение состояния, которое показано ниже.

${displaystyle {точка {p}} _ {3} (t) = e_ {3} (t) = e_ {1} (t) - {frac {R_ {2}} {I_ {3}}} cdot p_ { 3} (t) - {frac {r} {C_ {6}}} cdot q_ {6} (t)}$

Второе уравнение состояния также может быть решено, если вспомнить, что ${extstyle {точка {q}} _ {6} (t) = f_ {6} (t)}$. Второе уравнение состояния показано ниже.

${displaystyle {точка {q}} _ {6} (t) = f_ {6} (t) = {frac {r} {I_ {3}}} cdot p_ {3} (t) - {frac {1} {R_ {7} cdot C_ {6}}} cdot q_ {6} (t)}$

Оба уравнения могут быть преобразованы в матричную форму. Результат ниже.

${displaystyle {egin {bmatrix} {dot {p}} _ {3} (t) {dot {q}} _ {6} (t) end {bmatrix}} = {egin {bmatrix} - {frac {R_) {2}} {I_ {3}}} & - {frac {r} {C_ {6}}} {frac {r} {I_ {3}}} & - {frac {1} {R_ {7} cdot C_ {6}}} end {bmatrix}} {egin {bmatrix} p_ {3} (t) q_ {6} (t) end {bmatrix}} + {egin {bmatrix} 1 0end {bmatrix}} {egin {bmatrix} e_ {1} (t) end {bmatrix}}}$

На этом этапе уравнения можно рассматривать как любые другие представление в пространстве состояний проблема.

Международные конференции по моделированию графов облигаций (ECMS и ICBGM)

Библиографию по моделированию графа облигаций можно получить на следующих конференциях:

• ECMS-2013 27-я Европейская конференция по моделированию и симуляции, 27–30 мая 2013 г., Олесунн, Норвегия
• ECMS-2008 22-я Европейская конференция по моделированию и моделированию, 3–6 июня 2008 г. Никосия, Кипр
• ICBGM-2007: 8-я Международная конференция по моделированию и симуляции графов облигаций, 15–17 января 2007 г., Сан-Диего, Калифорния, США.
• ECMS-2006 20-я Европейская конференция по моделированию и моделированию, 28–31 мая 2006 г., Бонн, Германия
• IMAACA-2005 Международная мультиконференция по средиземноморскому моделированию
• Международная конференция ICBGM-2005 по моделированию и симуляции графов облигаций, 23–27 января 2005 г., Новый Орлеан, Луизиана, США. – Статьи
• ICBGM-2003 Международная конференция по моделированию и симуляции графов облигаций (ICBGM'2003) 19–23 января 2003 г., Орландо, Флорида, США – Статьи
• 14-й Европейский симпозиум по моделированию 23–26 октября 2002 г. Дрезден, Германия
• ESS'2001 13-й Европейский симпозиум по моделированию, Марсель, Франция, 18–20 октября 2001 г.
• ICBGM-2001 Международная конференция по моделированию и симуляции графов бондов (ICBGM 2001), Феникс, Аризона, США.
• European Simulation Multi-Conference 23-26 мая 2000 г., Гент, Бельгия
• 11-й Европейский симпозиум по моделированию, 26–28 октября 1999 г. Замок, Университет Фридриха-Александра, Эрланген-Нюрнберг, Германия
• ICBGM-1999 Международная конференция по моделированию и симуляции графов облигаций 17–20 января 1999 г. Сан-Франциско, Калифорния
• ESS-97 9-й Европейский симпозиум и выставка моделирования в промышленности, Пассау, Германия, 19–22 октября 1997 г.
• ICBGM-1997 3-я Международная конференция по моделированию и симуляции графов облигаций, 12–15 января 1997 г., Sheraton-Crescent Hotel, Феникс, Аризона
• 11-я Европейская симуляционная мультиконференция Стамбул, Турция, 1–4 июня 1997 г.
• ESM-1996 10-я ежегодная Европейская имитационная мультиконференция Будапешт, Венгрия, 2–6 июня 1996 г.
• ICBGM-1995 Int. Конф. по моделированию и моделированию графа облигаций (ICBGM’95), 15–18 января 1995 г., Лас-Вегас, Невада.

Смотрите также

• 20-сим программное обеспечение для моделирования на основе теории графов связей
• AMESim программное обеспечение для моделирования на основе теории графов связей
• Simscape Официальная дополнительная библиотека MATLAB / Simulink для графического программирования Bond Graph
• BG V.2.1 Бесплатная дополнительная библиотека MATLAB / Simulink для графического программирования Bond Graph
• График гибридной связи

Рекомендации

Примечания

дальнейшее чтение

• Кипурос, Хавьер (2013). Системная динамика и управление с помощью моделирования графа облигаций. Бока-Ратон: Тейлор и Фрэнсис. Дои:10.1201 / b14676. ISBN  978-1-4665-6075-8.
• Пейнтер, Генри М. (1960). Анализ и проектирование инженерных систем. M.I.T. Нажмите. ISBN  0-262-16004-8.
• Karnopp, Dean C .; Марголис, Дональд Л .; Розенберг, Рональд С. (1990). Системная динамика: единый подход. Нью-Йорк: Джон Вили и сыновья. ISBN  0-471-62171-4.
• Тома, Жан Ульрих (1975). Графики облигаций: введение и применение. Оксфорд: Pergamon Press. ISBN  0-08-018882-6.
• Gawthrop, Питер Дж .; Смит, Лоркан П. С. (1996). Метамоделирование: графы облигаций и динамические системы. Лондон: Прентис-Холл. ISBN  0-13-489824-9.
• Браун, Форбс Т. (2007). Динамика инженерных систем - единый графоцентрированный подход. Бока-Ратон: Тейлор и Фрэнсис. ISBN  0-8493-9648-4.
• Мукерджи, Амаленду; Кармакар, Ранджит (2000). Моделирование инженерных систем с помощью графов. Бока-Ратон: CRC Press. ISBN  978-0-8493-0982-3.
• Gawthrop, P.J .; Балланс, Д.Дж. (1999). «Глава 2: Символьные вычисления для управления иерархическими графами облигаций». В Манро, Н. (ред.). Символические методы в анализе и проектировании систем управления. Лондон: Институт инженеров-электриков. стр.23 -52. ISBN  0-85296-943-0.
• Боруцкий, Вольфганг (2010). Методология графа облигаций. Лондон: Спрингер. Дои:10.1007/978-1-84882-882-7. ISBN  978-1-84882-881-0.
• http://www.site.uottawa.ca/~rhabash/ESSModelFluid.pdf Объясняет моделирование графа связей в жидкой области.
• http://www.dartmouth.edu/~sullivan/22files/Fluid_sys_anal_w_chart.pdf Объясняет моделирование графа связей в жидкой области.