График потока сигналов - Signal-flow graph
А график потока сигналов или же сигнальный поток (SFG), изобретенный Клод Шеннон,[1] но часто называют Граф Мейсона после Сэмюэл Джефферсон Мейсон кто придумал термин,[2] специализированный граф потока, а ориентированный граф в котором узлы представляют системные переменные, а ветви (ребра, дуги или стрелки) представляют собой функциональные связи между парами узлов. Таким образом, теория графов потоков сигналов основана на теории ориентированные графы (также называемый диграфы ), который также включает ориентированные графы. Эта математическая теория орграфов существует, конечно, отдельно от ее приложений.[3][4]
SFG чаще всего используются для представления потока сигналов в физическая система и его контроллер (ы), образуя киберфизическая система. Среди других их применений - представление потока сигналов в различных электронных сетях и усилителях, цифровые фильтры, фильтры с переменным состоянием и некоторые другие типы аналоговых фильтров. Почти во всей литературе граф потока сигналов ассоциируется с система линейных уравнений.
История
Вай-Кай Чен писал: «Концепция графа потока сигналов была первоначально разработана Шеннон [1942][1] в работе с аналоговыми компьютерами. Наибольшую заслугу в построении графов потока сигналов обычно оказывают Мейсон [1953],[2] [1956].[5] Он показал, как использовать технику графа потока сигналов для решения некоторых сложных электронных задач относительно простым способом. Период, термин график потока сигналов был использован из-за его первоначального применения к электронным проблемам и связи с электронными сигналами и блок-схемами исследуемых систем ».[6]
Лоренс писал: «До Мейсон работа, К. Э. Шеннон[1] разработал ряд свойств того, что теперь известно как потоковые графы. К сожалению, документ изначально имел ограниченную классификацию, и очень немногие люди имели доступ к материалам ».[7]
«Правила вычисления определителя графа графа Мейсона были впервые даны и доказаны Шенноном [1942] с использованием математической индукции. Его работа оставалась практически неизвестной даже после того, как Мейсон опубликовал свою классическую работу в 1953 году. Три года спустя Мейсон [1956] ] заново открыл правила и доказал их, рассмотрев значение определителя и то, как оно изменяется при добавлении переменных в граф. [...] "[8]
Область применения
Робишо и другие. Определите область применения SFG следующим образом:[9]
- «Все физические системы, аналогичные этим сетям [построенные из идеальных трансформаторов, активных элементов и гираторов], составляют область применения разработанных [здесь] методов. Трент[10] показал, что в эту категорию попадают все физические системы, удовлетворяющие следующим условиям.
- Конечная система с сосредоточенными параметрами состоит из ряда простых частей, каждая из которых имеет известные динамические свойства, которые могут быть определены уравнениями с использованием двух типов скалярных переменных и параметров системы. Переменные первого типа представляют собой величины, которые могут быть измерены, по крайней мере, концептуально, путем присоединения показывающего прибора к двум точкам соединения элемента. Переменные второго типа характеризуют величины, которые можно измерить, последовательно подключив счетчик к элементу. Относительные скорости и положения, перепады давлений и напряжения являются типичными величинами первого класса, тогда как электрические токи, силы, скорости теплового потока - переменными второго типа. Firestone была первой, кто различил эти два типа переменных с помощью имен по переменным и через переменные.
- Переменные первого типа должны подчиняться сеточному закону, аналогичному закону напряжения Кирхгофа, тогда как переменные второго типа должны подчиняться закону инцидентности, аналогичному текущему закону Кирхгофа.
- Физические размеры соответствующих произведений переменных двух типов должны быть согласованы. Для систем, в которых выполняются эти условия, можно построить линейный граф, изоморфный динамическим свойствам системы, описываемым выбранными переменными. Эти методы [...] могут быть применены непосредственно к этим линейным графам, а также к электрическим сетям, чтобы получить граф потока сигналов системы ».
Основные концепции потокового графа
Следующая иллюстрация и ее значение были представлены Мэйсоном для иллюстрации основных понятий:[2]

В простых потоковых графах на рисунке функциональная зависимость узла обозначена входящей стрелкой, узел, вызывающий это влияние, является началом этой стрелки, и в самом общем виде граф потока сигналов указывает входящими стрелками только те узлы, которые влияют на обработку на принимающем узле, и на каждом узле, я, входящие переменные обрабатываются в соответствии с функцией, связанной с этим узлом, например Fя. Блок-граф в (а) представляет набор явных отношений:
Узел Икс1 является изолированным узлом, поскольку стрелка не поступает; уравнения для Икс2 и Икс3 имеют графики, показанные в частях (b) и (c) рисунка.
Эти отношения определяют для каждого узла функцию, которая обрабатывает входные сигналы, которые он получает. Каждый узел, не являющийся источником, каким-либо образом объединяет входные сигналы и передает результирующий сигнал по каждой исходящей ветви. «Потоковый граф, как первоначально определил Мэйсон, подразумевает набор функциональных отношений, линейных или нет».[9]
Однако обычно используемый граф Мейсона более ограничен, предполагая, что каждый узел просто суммирует свои входящие стрелки и что каждая ветвь включает только задействованный инициирующий узел. Таким образом, в этом более ограничительном подходе узел Икс1 не затрагивается, пока:
а теперь функции жij могут быть связаны с ветвями потока сигналов ij соединение пары узлов Икся, Иксj, а не общие отношения, связанные с каждым узлом. Вклад узла в себя как ж33 за Икс3 называется петля. Часто эти функции представляют собой просто мультипликативные факторы (часто называемые передачи или же прибыль), Например, жij(Иксj) = cijИксj, куда c является скаляром, но, возможно, является функцией некоторого параметра, например, переменной преобразования Лапласа s. Графики потока сигналов очень часто используются с сигналами, преобразованными по Лапласу, потому что тогда они представляют системы Линейные дифференциальные уравнения. В этом случае коэффициент пропускания, c (s), часто называют функция передачи.
Выбор переменных
В общем, есть несколько способов выбора переменных в сложной системе. В соответствии с каждым выбором система уравнений можно записать, и каждую систему уравнений можно представить в виде графика. Эта формулировка уравнений становится прямой и автоматической, если в распоряжении человека есть методы, позволяющие рисовать график непосредственно из принципиальная схема исследуемой системы. Структура полученных таким образом графиков просто связана с топология из принципиальная схема, и нет необходимости учитывать уравнения, даже неявно, чтобы получить график. В некоторых случаях нужно просто представить себе блок-схему на схематической диаграмме, и желаемые ответы можно получить, даже не нарисовав блок-схему.
— Робишо[11]
Неединственность
Robichaud et al. писал: «График потока сигналов содержит ту же информацию, что и уравнения, из которых он получен; но не существует взаимно однозначного соответствия между графиком и системой уравнений. Одна система будет давать разные графики в соответствии с порядок, в котором уравнения используются для определения переменной, записанной слева ".[9] Если все уравнения связывают все зависимые переменные, то есть п! возможные SFG на выбор.[12]
Линейные графики потока сигналов
Методы линейного графика потока сигналов (SFG) применимы только к линейные инвариантные во времени системы, как изучено их связанная теория. При моделировании интересующей системы первым шагом часто является определение уравнений, представляющих работу системы, без указания причин и следствий (это называется акаузальным моделированием).[13] Затем из этой системы уравнений выводится SFG.
Линейный SFG состоит из узлов, обозначенных точками, и взвешенных направленных ветвей, обозначенных стрелками. Узлы - это переменные уравнения а веса ветвей - это коэффициенты. Сигналы могут пересекать ветку только в направлении, указанном ее стрелкой. Элементы SFG могут представлять только операции умножения на коэффициент и сложения, которых достаточно для представления уравнений с ограничениями. Когда сигнал пересекает ветвь в указанном направлении, сигнал умножается на вес ветви. Когда две или более ветви направляются в один и тот же узел, их выходы добавляются.
Для систем, описываемых линейными алгебраическими или дифференциальными уравнениями, граф потока сигналов математически эквивалентен системе уравнений, описывающей систему, и уравнения, управляющие узлами, обнаруживаются для каждого узла путем суммирования входящих ветвей к этому узлу. Эти входящие ветви передают вклады других узлов, выраженные как значение подключенного узла, умноженное на вес соединительной ветви, обычно действительное число или функцию некоторого параметра (например, Преобразование Лапласа Переменная s).
Для линейных активных сетей Чома пишет:[14] «Под« представлением потока сигнала »[или« графиком », как его обычно называют] мы подразумеваем диаграмму, которая, отображая алгебраические отношения между соответствующими переменными ветвления сети, рисует однозначную картину того, как применяется входной сигнал. "потоки" из портов ввода-вывода ... ".
Мотивация для анализа SFG описана Ченом:[15]
- «Анализ линейной системы в конечном итоге сводится к решению системы линейных алгебраических уравнений. В качестве альтернативы обычным алгебраическим методам решения системы можно получить решение, рассматривая свойства определенных ориентированных графов, связанных с система." [См. Подраздел: Решение линейных уравнений.] "Неизвестные в уравнениях соответствуют узлам графа, в то время как линейные отношения между ними проявляются в виде направленных ребер, соединяющих узлы. ... Связанные ориентированные графы во многих случаях могут быть установлены непосредственно путем проверки физической системы без необходимости сначала формулировать â † 'связанные уравнения ... "
Основные компоненты

Линейный график потока сигналов связан с системой линейных уравнений[16] следующего вида:
- куда = коэффициент пропускания (или усиление) от к .
На рисунке справа изображены различные элементы и конструкции графа потока сигналов (SFG).[17]
- Экспонат (а) представляет собой узел. В этом случае узел помечен . Узел - это вершина, представляющая переменную или сигнал.
- А источник узел имеет только исходящие ветви (представляет собой независимую переменную). В частном случае Вход узел характеризуется наличием одной или нескольких прикрепленных стрелок, указывающих от узла и нет стрелки, указывающие на узел. Любая открытая полная SFG будет иметь по крайней мере один входной узел.
- An выход или же раковина узел имеет только входящие ветви (представляет собой зависимую переменную). Хотя любой узел может быть выходом, для ясности часто используются явные выходные узлы. Узлы явного вывода характеризуются наличием одной или нескольких прикрепленных стрелок, указывающих на узел, и нет стрелки, указывающие от узла. Явные выходные узлы не требуются.
- А смешанный узел имеет как входящие, так и исходящие ветви.
- Экспонат (б) представляет собой ветвь с мультипликативным усилением . Это означает, что результат на конце стрелки умноженный на ввод в хвосте стрелки. Коэффициент усиления может быть простой константой или функцией (например: функцией некоторой переменной преобразования, такой как , , или же , для соотношений Лапласа, Фурье или Z-преобразования).
- Рисунок (c) - это ветвь с мультипликативным усилением, равным единице. Если коэффициент усиления не указан, предполагается, что он равен единице.
- Экспонат (d) является входным узлом. В этом случае, умножается на выигрыш .
- Приложение (е) явный выходной узел; входящий край имеет усиление .
- Приложение (f) изображает добавление. Когда две или более стрелки указывают на узел, сигналы, переносимые ребрами, складываются.
- На рисунке (g) изображена простая петля. Коэффициент усиления контура .
- На рисунке (h) изображено выражение .
Термины, используемые в линейной теории SFG, также включают:[17]
- Дорожка. Путь - это непрерывный набор ветвей, пересекаемых в направлении, указанном стрелками ветвей.
- Открытый путь. Если ни один узел не посещается повторно, путь открыт.
- Прямой путь. Путь от входного узла (источника) к выходному узлу (приемнику), который не посещает повторно ни один узел.
- Усиление пути: продукт прибылей всех ветвей на пути.
- Петля. Закрытый путь. (он начинается и заканчивается в одном и том же узле, и ни один узел не затрагивается более одного раза).
- Коэффициент усиления петли: произведение прироста всех ветвей в петле.
- Бесконтактные петли. Бесконтактные петли не имеют общих узлов.
- Редукция графика. Удаление одного или нескольких узлов из графа с помощью преобразований графа.
- Остаточный узел. В любом предполагаемом процессе сокращения графа узлы, которые должны быть сохранены в новом графе, называются остаточными узлами.[2]
- Разделение узла. Разделение узла соответствует разделению узла на два полуузла, один из которых является приемником, а другой - источником.[18]
- Индекс: Индекс графа - это минимальное количество узлов, которые должны быть разделены, чтобы удалить все петли в графе.
- Индексный узел. Узлы, которые разделяются для определения индекса графа, называются индекс узлов, и в целом они не уникальны.
Систематическое сокращение до источников и поглотителей
Граф потока сигналов можно упростить с помощью правил преобразования графа.[19][20][21] Эти правила упрощения также называются алгебра графов потоков сигналов.[22]Цель этого сокращения - связать интересующие зависимые переменные (остаточные узлы, стоки) с его независимыми переменными (источниками).
Систематическое сокращение линейного графика потока сигналов - это графический метод, эквивалентный Исключение Гаусса-Джордана метод решения линейных уравнений.[23]
Представленные ниже правила могут применяться снова и снова, пока граф потока сигналов не будет приведен к его «минимальной остаточной форме». Дальнейшее сокращение может потребовать исключения цикла или использования «формулы сокращения» с целью прямого соединения узлов-приемников, представляющих зависимые переменные, с узлами-источниками, представляющими независимые переменные. Таким образом, любой граф потока сигналов может быть упрощен путем последовательного удаления внутренних узлов до тех пор, пока не останутся только входные, выходные и индексные узлы.[24][25] Робишо описал этот процесс систематического сокращения потокового графа:
Сокращение графа происходит путем исключения определенных узлов, чтобы получить остаточный граф, показывающий только интересующие переменные. Это устранение узлов называется "узел поглощения". Этот метод близок к известному процессу последовательного исключения нежелательных переменных в системе уравнений. Можно исключить переменную, удалив соответствующий узел в графе. Если достаточно уменьшить граф, можно получить решение для любой переменной, и это цель, которую мы будем иметь в виду в этом описании различных методов сокращения графа. Однако на практике методы сокращения будут использоваться исключительно для преобразования графа в остаточный граф, выражающий некоторые фундаментальные отношения. Полные решения будут легче получить, применяя Правило масона.[26]Сам график программирует процесс редукции. Действительно, простой просмотр графика легко подсказывает различные шаги редукции, которые выполняются элементарными преобразованиями, устранением петель или использованием формулы редукции.[26]
— Робишо, Графики потоков сигналов и приложения, 1962 г.
Для цифрового сокращения потокового графа с помощью алгоритма Робишо расширяет понятие простого потокового графа до обобщенный граф потока:
Прежде чем описывать процесс редукции ... соответствие между графиком и системой линейных уравнений ... необходимо обобщить ...Обобщенные графики будут представлять некоторые рабочие отношения между группами переменных.... С каждой ветвью обобщенного графа связана матрица, задающая отношения между переменными, представленными узлами на концах этой ветви ...[27]Элементарные преобразования [определенные Робишо на его рис. 7.2, с. 184], а сокращение цикла позволяет исключить любой узел j графа формула приведения: [описано в уравнении Робишо 7-1]. С помощью формулы редукции всегда можно уменьшить граф любого порядка ... [После редукции] конечный граф будет каскадным графом, в котором переменные узлов-приемников явно выражены как функции источников. Это единственный метод сокращения обобщенного графа, так как правило Мейсона явно неприменимо.[28]
— Робишо, Графики потоков сигналов и приложения, 1962 г.
Определение элементарное преобразование варьируется от автора к автору:
- Некоторые авторы рассматривают только как элементарные преобразования суммирование усилений параллельных фронтов и умножение усилений последовательных фронтов, но не устранение петель.[23][29]
- Другие авторы рассматривают устранение петли как элементарное преобразование.[30]
Параллельные края. Замените параллельные кромки одной кромкой с коэффициентом усиления, равным сумме исходных коэффициентов усиления.

Граф слева имеет параллельные ребра между узлами. Справа эти параллельные ребра были заменены одним ребром, имеющим усиление, равное сумме усилений на каждом исходном ребре.
Уравнения, соответствующие редукции между N и узел я1 находятся:
Вытекающие края. Замените исходящие ребра ребрами, исходящими непосредственно из источников узла.
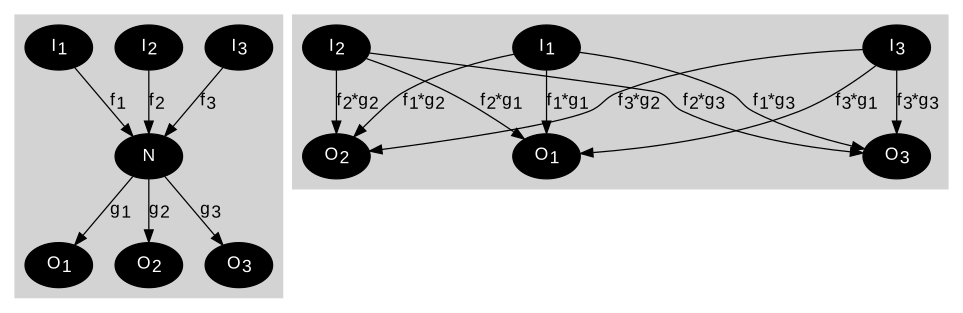
График слева имеет промежуточный узел N между узлами, из которых он имеет приток, и узлами, к которым он вытекает. График справа показывает прямые потоки между этими наборами узлов, без перехода через N.
Ради простоты, N и его притоки не представлены. Отток из N устранены.
Уравнения, соответствующие редукции, непосредственно связывающие N 's входные сигналы к его выходным сигналам:
Узлы с нулевым сигналом.
Устранение выходящих ребер из узла, для которого определено нулевое значение.

Если значение узла равно нулю, его выходящие ребра могут быть устранены.
Узлы без оттоков.
Устранить узел без оттоков.

В этом случае, N не представляет интереса и не имеет исходящих ребер; следовательно, N, и его входящие края, могут быть устранены.
Самоклеящийся край. Замените края петель, отрегулировав усиление на входящих краях.

Граф слева имеет зацикленное ребро в узле N, с приростом грамм. Справа кромка петли удалена, а коэффициент усиления всех входящих кромок делится на (1-г).
Уравнения, соответствующие редукции между N и все его входные сигналы:
Реализации
Вышеописанная процедура построения SFG из акаузальной системы уравнений и решения коэффициентов усиления SFG была реализована.[31] как дополнение к MATHLAB 68,[32] он-лайн система, обеспечивающая машинную помощь для механических символических процессов, встречающихся в анализе.
Решение линейных уравнений
Графики прохождения сигналов могут использоваться для решения систем одновременных линейных уравнений.[33] Система уравнений должна быть согласованной, и все уравнения должны быть линейно независимыми.
Приведение уравнений в "стандартную форму"

Для M уравнений с N неизвестными, где каждое yj известное значение, и каждый xj - неизвестное значение, для каждого известного имеется уравнение следующего вида.
- ; обычная форма для одновременных линейных уравнений с 1 ≤ j ≤ M
Хотя возможно, особенно для простых случаев, построить граф потока сигналов с использованием уравнений в этой форме, некоторые изменения позволяют общую процедуру, которая легко работает для любого набора уравнений, как это представлено сейчас. Чтобы продолжить, сначала уравнения переписываются как
и далее переписывается как
и, наконец, переписан как
- ; форма, подходящая для выражения в виде графика потока сигналов.
- где δкДж = Дельта Кронекера
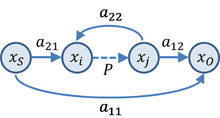
Граф потока сигналов теперь организован путем выбора одного из этих уравнений и адресации узла в правой части. Это узел, для которого узел соединяется с самим собой ветвью веса, включающей '+1', образуя петля в потоковом графе. Другие члены в этом уравнении сначала связывают этот узел с источником в этом уравнении, а затем со всеми другими ветвями, входящими в этот узел. Таким образом обрабатывается каждое уравнение, а затем каждая инцидентная ветвь присоединяется к соответствующему исходящему узлу. Например, на рисунке показан случай трех переменных, а первое уравнение выглядит следующим образом:
где правая часть этого уравнения представляет собой сумму взвешенных стрелок, падающих на узел Икс1.
Поскольку в обработке каждого узла существует базовая симметрия, простая отправная точка - это расположение узлов, при котором каждый узел находится в одной вершине правильного многоугольника. При выражении с использованием общих коэффициентов {cв}, тогда среда каждого узла будет такой же, как и все остальные, за исключением перестановки индексов. Такая реализация для системы из трех одновременных уравнений показана на рисунке.[34]
Часто известные значения yj принимаются в качестве первопричин, а неизвестные значения xj быть эффектами, но независимо от этой интерпретации, последняя форма для системы уравнений может быть представлена как граф потока сигналов. Этот момент обсуждается далее в подразделе Интерпретация причинности.
Применение формулы усиления Мейсона
В самом общем случае значения для всех xk переменные могут быть вычислены путем вычисления формулы усиления Мейсона для пути от каждого yj каждому хk и используя суперпозицию.
- где GкДж = сумма формулы усиления Мэйсона, вычисленная для всех путей от входа yj к переменной xk.
В общем, есть N-1 путей из yj к переменной xk поэтому вычислительные затраты на вычисление GкДж пропорциональна N-1, поскольку существует M значений yj, ГРАММкДж должно быть вычислено M раз для одного значения xk. Вычислительные затраты на вычисление одного xk переменная пропорциональна (N-1) (M). Усилия по вычислению всех xk переменные пропорциональны (N) (N-1) (M). Если имеется N уравнений и N неизвестных, то объем вычислений составляет порядка N3.
Отношение к блок-схемам
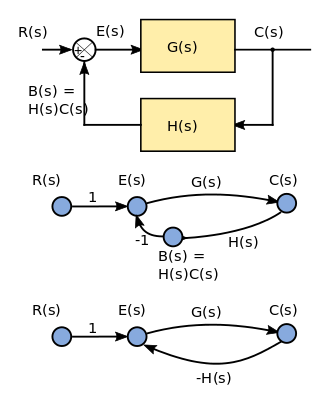
По мнению некоторых авторов, линейный график потока сигналов более ограничен, чем блок-схема,[35] в том, что SFG строго описывает линейные алгебраические уравнения, представленные ориентированным графом.
Для других авторов линейные блок-схемы и линейные графики потока сигналов являются эквивалентными способами изображения системы, и любой из них может использоваться для определения коэффициента усиления.[36]
Таблица сравнения блок-схем и диаграмм потока сигналов предоставлена Bakshi & Bakshi,[37] и другая таблица Кумара.[38] По словам Баркера и другие.:[39]
- «Граф потока сигналов - наиболее удобный метод для представления динамической системы. Топология графа компактна, и правила для управления им легче запрограммировать, чем соответствующие правила, которые применяются к блок-схемам».
На рисунке представлена простая блок-схема для Обратная связь Система показана с двумя возможными интерпретациями как граф потока сигналов. Вход R (s) - входной сигнал с преобразованием Лапласа; он показан как узел-источник в графе потока сигналов (узел-источник не имеет входных ребер). Выходной сигнал C (s) - выходная переменная после преобразования Лапласа. На блок-схеме он представлен как приемный узел (приемник не имеет выходных ребер). G (s) и H (s) передаточные функции, с H (s) служащая для обратной связи измененной версии вывода на ввод, B (s). Два представления потокового графа эквивалентны.
Интерпретация причинности
Термин «причина и следствие» был применен Мейсоном к SFG:[2]
- «Процесс построения графа - это процесс отслеживания последовательности причин и следствий в физической системе. Одна переменная выражается как явное следствие, вызванное определенными причинами; они, в свою очередь, распознаются как следствия, обусловленные еще и другими причинами».
- - С.Дж. Мейсон: Раздел IV: Иллюстративные приложения техники потоковых графов
и был повторен многими более поздними авторами:[40]
- "The график потока сигналов - еще один визуальный инструмент для представления причинно-следственных связей между компонентами системы. Это упрощенная версия блок-схемы, представленной С.Дж. Мейсон как причинно-следственное представление линейных систем ».
- - Артур Г.О. Мутамбара: Проектирование и анализ систем управления, стр.238
Тем не менее, статья Мэйсона призвана подробно показать, как система уравнений связан с SFG, акцент, не связанный с интуитивными понятиями «причина и следствие». Интуиция может быть полезна для достижения SFG или для понимания SFG, но несущественна для SFG. Существенная связь SFG с его собственным набором уравнений, как описано, например, Огатой:[41]
- «График потока сигналов - это диаграмма, которая представляет собой набор одновременных алгебраических уравнений. При применении метода графа потоков сигналов к анализу систем управления мы должны сначала преобразовать линейные дифференциальные уравнения в алгебраические уравнения в [ Преобразование Лапласа Переменная] s.."
- - Кацухико Огата: Современная контрольная техника, п. 104
Здесь нет ссылки на «причину и следствие», и, как сказал Баруцкий:[42]
- «Подобно блок-схемам, графы потоков сигналов представляют вычислительную, а не физическую структуру системы».
- - Вольфганг Боруцки, Методология графа облигаций, п. 10
Термин «причина и следствие» может быть неверно истолкован, поскольку он применяется к SFG, и неправильно использован, чтобы предложить системный взгляд на причинность,[43] а не вычислительно основанный на значении. Чтобы обсуждение оставалось ясным, может быть целесообразно использовать термин «вычислительная причинность», как это предлагается для графики облигаций:[44]
- «В литературе по графу Бонда используется термин вычислительная причинность, обозначающий порядок вычислений в моделировании, чтобы избежать любой интерпретации в смысле интуитивной причинности».
Термин «вычислительная причинность» объясняется на примере тока и напряжения в резисторе:[45]
- "The вычислительная причинность физических законов поэтому не может быть предопределено, но зависит от конкретного использования этого закона. Мы не можем сделать вывод, вызывает ли падение напряжения ток, протекающий через резистор, или же разность потенциалов на двух концах резистора вызывает протекание тока. Физически это просто два параллельных аспекта одного и того же физического явления. С точки зрения вычислений нам, возможно, придется иногда принимать одно положение, а иногда другое ".
- - Франсуа Селье и Эрнесто Кофман: §1.5 Программное обеспечение для моделирования сегодня и завтра, п. 15
Компьютерная программа или алгоритм могут быть настроены для решения набора уравнений с использованием различных стратегий. Они различаются тем, как они расставляют приоритеты при нахождении некоторых переменных с точки зрения других, и эти алгоритмические решения, которые просто касаются стратегии решения, затем устанавливают переменные, выраженные как зависимые переменные ранее в решении, как «эффекты», определяемые остальные переменные, которые теперь являются «причинами» в смысле «вычислительной причинности».
Используя эту терминологию, это вычислительный причинность, а не система причинно-следственная связь, относящаяся к SFG. Существует широкая философская дискуссия, не связанная конкретно с SFG, по поводу связи между вычислительной причинностью и системной причинностью.[46]
Графики потока сигналов для анализа и проектирования
Графики потока сигналов могут использоваться для анализа, то есть для понимания модели существующей системы, или для синтеза, то есть для определения свойств альтернативного проекта.
Графики потока сигналов для анализа динамических систем
При построении модели динамической системы Dorf & Bishop предоставляет список шагов:[47]
- Определите систему и ее компоненты.
- Сформулируйте математическую модель и перечислите необходимые предположения.
- Напишите дифференциальные уравнения, описывающие модель.
- Решите уравнения для требуемых выходных переменных.
- Изучите решения и предположения.
- Если необходимо, повторно проанализируйте или измените структуру системы.
- —RC Дорф и Р. Х. Бишоп, Современные системы управления, Глава 2, с. 2
В этом рабочем процессе уравнения математической модели физической системы используются для вывода уравнений графа потока сигналов.
Графики потока сигналов для синтеза дизайна
Графики потока сигналов использовались в Дизайн космических исследований (DSE), как промежуточное представление о физической реализации. Процесс DSE ищет подходящее решение среди различных альтернатив. В отличие от типичного рабочего процесса анализа, когда интересующая система сначала моделируется с помощью физических уравнений ее компонентов, спецификация для синтеза конструкции может быть желаемой передаточной функцией. Например, разные стратегии будут создавать разные графы потоков сигналов, из которых выводятся реализации.[48]В другом примере аннотированный SFG используется как выражение поведения в непрерывном времени в качестве входных данных для генератора архитектуры.[49]
Формулы Шеннона и Шеннона-Хаппа
Формула Шеннона - это аналитическое выражение для расчета коэффициента усиления взаимосвязанного набора усилителей в аналоговом компьютере. Во время Второй мировой войны, исследуя функциональную работу аналогового компьютера, Клод Шеннон разработал свою формулу. Из-за ограничений военного времени работа Шеннона в то время не была опубликована, а в 1952 г. Мейсон заново открыл ту же формулу.
Хапп обобщил формулу Шеннона для топологически замкнутых систем.[50] Формула Шеннона-Хаппа может использоваться для получения передаточных функций, чувствительности и функций ошибок.[51]
Для согласованного набора линейных односторонних отношений формула Шеннона-Хаппа выражает решение с использованием прямой подстановки (неитеративной).[51][52]
Программное обеспечение НАСА для электрических схем NASAP основано на формуле Шеннона-Хаппа.[51][52]
Примеры линейного графика потока сигналов
Простой усилитель напряжения

Усиление сигнала V1 усилителем с усилением а12 математически описывается
Эта взаимосвязь, представленная графиком потока сигналов на рисунке 1., состоит в том, что V2 зависит от V1 но это не подразумевает зависимости от V1 на V2. См. Страницу Коу 57.[53]
Идеальный усилитель с отрицательной обратной связью
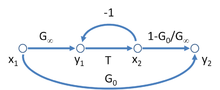

Возможный SFG для модель асимптотического выигрыша для усилитель отрицательной обратной связи показан на рисунке 3, и приводит к уравнению для усиления этого усилителя как
Расшифровка параметров следующая: Т = коэффициент возврата, грамм∞ = коэффициент усиления прямого усилителя, грамм0 = feedforward (с указанием возможных двусторонний характер обратной связи, возможно, преднамеренный, как в случае прямой связи компенсация ). На рисунке 3 есть интересный аспект: он похож на рисунок 2 для двухпортовой сети с добавлением дополнительных обратная связь Икс2 = T y1.
Из этого выражения усиления интерпретация параметров грамм0 и грамм∞ очевидно, а именно:
Есть много возможных SFG, связанных с любым конкретным соотношением усиления. На рисунке 4 показан еще один SFG для модели асимптотического усиления, который легче интерпретировать в терминах схемы. На этом графике параметр β интерпретируется как коэффициент обратной связи и А как «управляющий параметр», возможно, связанный с зависимым источником в цепи. Используя этот график, коэффициент усиления равен
Для подключения к модели асимптотического усиления параметры А и β не могут быть произвольными параметрами схемы, но должны относиться к коэффициенту возврата Т к:
и к асимптотическому усилению как:
Подставляя эти результаты в выражение усиления,
что является формулой модели асимптотического усиления.
Электрическая схема, содержащая двухпортовую сеть

На рисунке справа изображена схема, содержащая у-параметрическая двухпортовая сеть. Vв - вход схемы, а V2 это выход. Двухпортовые уравнения накладывают набор линейных ограничений между напряжениями и токами на портах. Терминальные уравнения накладывают другие ограничения. Все эти ограничения представлены в SFG (график потока сигналов) под схемой. Есть только один путь от входа к выходу, который показан другим цветом и имеет коэффициент усиления (по напряжению) -R.Lу21. Также есть три петли: -Rву11, -РLу22, Рву21рLу12. Иногда цикл указывает на преднамеренную обратную связь, но он также может указывать на ограничение связи двух переменных. Например, уравнение, описывающее резистор, гласит, что отношение напряжения на резисторе к току через резистор является постоянной величиной, которая называется сопротивлением. Это можно интерпретировать как напряжение - это вход, а ток - это выход, или ток - это вход, а напряжение - выход, или просто то, что напряжение и ток имеют линейную зависимость. Практически все два пассивных оконечных устройства в цепи будут отображаться в SFG как петли.
SFG и схема изображают одну и ту же схему, но схема также предлагает назначение схемы. По сравнению со схемой, SFG неудобен, но имеет то преимущество, что усиление от входа к выходу может быть записано путем проверки с использованием Правило масона.
Мехатроника: сервопривод положения с многоконтурной обратной связью

Этот пример представляет собой SFG (граф потока сигналов), используемый для представления системы сервоуправления, и иллюстрирует некоторые особенности SFG. Некоторые из петель (петля 3, петля 4 и петля 5) являются внешними, специально разработанными петлями обратной связи. Они показаны пунктирными линиями. Существуют также внутренние циклы (цикл 0, цикл1, цикл2), которые не являются преднамеренными циклами обратной связи, хотя их можно анализировать, как если бы они были. Эти петли показаны сплошными линиями. Петля 3 и петля 4 также известны как второстепенные петли, потому что они находятся внутри более крупной петли.
- Прямой путь начинается с θC, желаемая команда положения. Это умножается на Kп которая может быть постоянной или функцией частоты. Kп включает коэффициент преобразования ЦАП и любую фильтрацию на выходе ЦАП. Выход Kп это команда скорости VωC которая умножается на KV которая может быть постоянной или функцией частоты. Выход KV это текущая команда, VIC которая умножается на KC которая может быть постоянной или функцией частоты. Выход KC - выходное напряжение усилителя, VА. Электрический ток, яM, хотя обмотка двигателя представляет собой интеграл напряжения, приложенного к индуктивности. Мотор выдает крутящий момент, Т, пропорционально яM. Двигатели с постоянными магнитами имеют тенденцию иметь линейную функцию тока к крутящему моменту. Константа преобразования тока в крутящий момент равна KM. Крутящий момент, Т, деленное на момент инерции нагрузки, M, - ускорение, α, который интегрируется для получения скорости нагрузки ω который интегрирован для определения положения нагрузки, θLC.
- Прямой путь контура 0 утверждает, что ускорение пропорционально крутящему моменту, а скорость является интегралом ускорения по времени. Обратный путь говорит о том, что по мере увеличения скорости возникает трение или сопротивление, которое противодействует крутящему моменту. Крутящий момент на нагрузке уменьшается пропорционально скорости нагрузки, пока не будет достигнута точка, в которой весь крутящий момент используется для преодоления трения, а ускорение упадет до нуля. Цикл 0 является внутренним.
- Loop1 представляет собой взаимодействие тока индуктора с его внутренним и внешним последовательным сопротивлением. Ток через индуктивность - это интеграл по времени от напряжения на индуктивности. Когда напряжение подается впервые, все оно появляется на катушке индуктивности. Об этом свидетельствует прямой путь через . По мере увеличения тока на внутреннем сопротивлении индуктора R падает напряжение.M а внешнее сопротивление RS. Это снижает напряжение на катушке индуктивности и представлено цепью обратной связи - (RM + RS). Ток продолжает увеличиваться, но с неуклонно уменьшающейся скоростью, пока ток не достигнет точки, в которой все напряжение падает на (RM + RS). Цикл 1 является внутренним.
- Loop2 выражает эффект обратной ЭДС двигателя. Когда двигатель с постоянными магнитами вращается, он действует как генератор и создает напряжение в его обмотках. Не имеет значения, вызвано ли вращение крутящим моментом, приложенным к приводному валу, или током, приложенным к обмоткам. Это напряжение называется обратной ЭДС. Коэффициент преобразования скорости вращения в обратную ЭДС составляет GM. Полярность обратной ЭДС такова, что она снижает напряжение на индуктивности обмотки. Цикл 2 является внутренним.
- Петля 3 является внешней. Ток в обмотке двигателя проходит через чувствительный резистор. Напряжение, VЯ, сформированный через резистор считывания, подается обратно на отрицательный вывод усилителя мощности KC. Эта обратная связь заставляет усилитель напряжения действовать как источник тока, управляемый напряжением. Поскольку крутящий момент двигателя пропорционален току двигателя, подсистема VIC выходной крутящий момент действует как источник крутящего момента, управляемый напряжением. Эта подсистема может называться «токовый контур» или «контур крутящего момента». Петля 3 эффективно снижает влияние петли 1 и петли 2.
- Петля 4 является внешней. Тахометр (на самом деле генератор постоянного тока малой мощности) выдает выходное напряжение VωM что пропорционально угловой скорости. Это напряжение подается на отрицательный вход KV. Эта обратная связь заставляет подсистему от VωC к угловой скорости нагрузки, чтобы действовать как источник напряжения для скорости. Эта подсистема может называться «контуром скорости». Цикл 4 эффективно уменьшает влияние цикла 0 и цикла 3.
- Петля 5 - внешняя. Это общий контур обратной связи по положению. Обратная связь поступает от углового энкодера, который выдает цифровой выход. Выходное положение вычитается из желаемого положения цифровым оборудованием, которое управляет ЦАП, который управляет Kп. В SFG коэффициент преобразования ЦАП включен в Kп.
Видеть Правило масона для разработки формулы усиления Мейсона для этого примера.
Терминология и классификация сигнальных графов
В литературе существует некоторая путаница относительно того, что такое граф потока сигналов; Генри Пейнтер, изобретатель графики облигаций, пишет: «Но большая часть упадка графов потока сигналов [...] отчасти объясняется ошибочным представлением о том, что ветви должны быть линейными, а узлы - суммативными. Сам Мейсон не принял ни одного из предположений!»[55]
Стандарты, охватывающие графики потока сигналов
- IEEE Std 155-1960, Стандарты IEEE для цепей: определения терминов для графов линейных потоков сигналов, 1960.
- Этот стандарт IEEE определяет график потока сигналов как сеть из направленные ветви представляя зависимых и независимых сигналы в качестве узлы. Входящие отделения несут сигналы ответвления к сигналам зависимого узла. А зависимый узел signal - это алгебраическая сумма входящих сигналов ветвления в этом узле, то есть узлы являются суммативными.
График потока сигналов перехода состояний
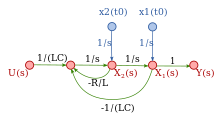
А состояние перехода SFG или же диаграмма состояний представляет собой диаграмму моделирования для системы уравнений, включающей начальные условия состояний.[56]
Замкнутый флоуграф

Замкнутые потоковые графы описывают замкнутые системы и используются для обеспечения строгой теоретической основы топологических методов анализа схем.[50]
- Терминология теории замкнутых потоковых графов включает:
- Вкладной узел. Точка суммирования для двух или более входящих сигналов, в результате чего получается только один исходящий сигнал.
- Распределительный узел. Точка выборки для двух или более исходящих сигналов, являющихся результатом только одного входящего сигнала.
- Составной узел. Сужение контрибутивного узла и распределительного узла.
- Строго зависимый и строго независимый узел. Строго независимый узел представляет собой независимый источник; строго зависимый узел представляет собой метр.
- Открытые и закрытые потоковые диаграммы. Открытый потоковый граф содержит строго зависимые или строго независимые узлы; в противном случае это замкнутый потоковый граф.
Нелинейные потоковые графы
Мейсон представил как нелинейные, так и линейные потоковые графы. Чтобы прояснить этот момент, Мейсон написал: «Линейный потоковый граф - это такой граф, уравнения которого линейны».[2]
Примеры нелинейных функций ветвления
Обозначим его через Иксj сигнал в узле j, ниже приведены примеры узловых функций, которые не относятся к линейная инвариантная во времени система:
Примеры моделей нелинейного графа потока сигналов
- Хотя они, как правило, не могут быть преобразованы между представлениями во временной и частотной областях для анализа классической теории управления, нелинейные графики потока сигналов можно найти в электротехнической литературе.[57][58]
- Нелинейные графики потока сигналов также можно найти в биологических науках, например, Dr Артур Гайтон Модель сердечно-сосудистой системы.[59]
Применение техники SFG в различных областях науки
- Электронные схемы
- Характеризуя последовательные схемы Мур и Мили тип, получение обычные выражения из диаграммы состояний.[60]
- Синтез нелинейных преобразователей данных[58]
- Теория управления и сети
- Стохастическая обработка сигналов.[61]
- Надежность электронных систем[62]
- Физиология и биофизика
- Регуляция сердечного выброса[63]
- Моделирование
- Моделирование на аналоговых компьютерах[64]
Смотрите также
- Модель асимптотического выигрыша
- Графики облигаций
- График Коутса
- Системы управления / схемы прохождения сигналов в системах управления Викибук
- Граф потока (математика)
- Фильтр чехарда для примера конструкции фильтра с использованием графа потока сигналов
- Формула усиления Мейсона
- Незначительная обратная связь петли
- Некоммутативный граф потока сигналов
Примечания
- ^ а б c CE Шеннон (январь 1942 г.). «Теория и проектирование машин линейных дифференциальных уравнений». Управление огнем Исследовательского комитета национальной обороны США: отчет 411, раздел D-2. Цитировать журнал требует
| журнал =(помощь) Перепечатано в Н. Дж. А. Слоан; Аарон Д. Виннер, ред. (1993). Клод Э. Шеннон: Сборник статей. Wiley IEEE Press. п. 514. ISBN 978-0-7803-0434-5. - ^ а б c d е ж Мейсон, Сэмюэл Дж. (Сентябрь 1953 г.). «Теория обратной связи - некоторые свойства графов прохождения сигналов» (PDF). Труды IRE. 41 (9): 1144–1156. Дои:10.1109 / jrproc.1953.274449. S2CID 17565263.
График потока можно интерпретировать как систему передачи сигнала, в которой каждый узел представляет собой крошечную станцию ретранслятора. Станция принимает сигналы через входящие ветви, каким-то образом объединяет информацию, а затем передает результаты по каждой исходящей ветви.
- ^ Йорген Банг-Йенсен; Григорий З. Гутин (2008). Диграфы. Springer. ISBN 9781848009981.
- ^ Бела Боллобас (1998). Современная теория графов. Springer Science & Business Media. п. 8. ISBN 9781461206194.я
- ^ SJ Mason (июль 1956 г.). "Теория обратной связи - дополнительные свойства графов потоков сигналов". Труды IRE. 44 (7): 920–926. Дои:10.1109 / JRPROC.1956.275147. HDL:1721.1/4778. S2CID 18184015. Он-лайн версия найдена на Исследовательская лаборатория электроники MIT.
- ^ Чен, Вай-Кай (1976). Прикладная теория графов: графы и электрические сети. Эльзевир. ISBN 9781483164151.(WKC 1976, п. 167)
- ^ Лоренс, Чарльз Стэнтон (15 июля 1956 г.), Фогель, Дэн (ред.), Технический отчет 317 - Теория и приложения потоковых графов (PDF), Исследовательская лаборатория электроники, Массачусетский технологический институт
- ^ (WKC 1976, п. 169)
- ^ а б c Луи П.А. Робишо; Морис Буазверт; Жан Роберт (1962). "Предисловие". Графики потоков сигналов и приложения. Прентис Холл. п. Икс. КАК В B0000CLM1G.
- ^ Гораций Трент (1955). «Изоморфизмы между ориентированными линейными графами и физическими системами с сосредоточенными параметрами». Журнал Акустического общества Америки. 27 (3): 500–527. Bibcode:1955ASAJ ... 27..500T. Дои:10.1121/1.1907949.
- ^ (Робишо 1962, п. ix)
- ^ Нарсинг Део (2004). Теория графов с приложениями в инженерии и информатике. PHI Learning Pvt. ООО п. 418. ISBN 9788120301450.
- ^ Кофранек, Дж; Mateják, M; Privitzer, P; Трибула, М (2008), Причинно-следственное или акаузальное моделирование: труд для людей или труд для машин (PDF), Технические вычисления, Прага, 2008. Материалы конференции., Прага, с. 16, заархивировано оригинал (PDF) на 2009-12-29
- ^ Дж. Чома-младший (апрель 1990 г.). «Анализ потока сигналов в сетях обратной связи». Транзакции IEEE в схемах и системах. 37 (4): 455–463. Bibcode:1990ITCS ... 37..455C. Дои:10.1109/31.52748.
- ^ Вай-Кай Чен (1971). «Глава 3: Решения линейных алгебраических уравнений с направленным графом». Прикладная теория графов. Паб Северная Голландия. Co. p. 140. ISBN 978-0444101051. Частично доступен с использованием Возможность заглянуть внутрь Amazon.
- ^ См., Например, Кацухико Огата (2004). "Глава 3-9: Графическое представление потоков сигналов линейных систем". Современная контрольная техника (4-е изд.). Прентис Холл. стр.106 ff. ISBN 978-0130609076. Однако однозначного соответствия не бывает: Нарсинг Део (2004). Теория графов с приложениями в инженерии и информатике. PHI Learning Pvt. ООО п. 418. ISBN 9788120301450.
- ^ а б Куо, Бенджамин С. (1967). Системы автоматического управления (2-е изд.). Прентис-Холл. С. 59–60.
- ^ Луи П.А. Робишо; Морис Буазверт; Жан Роберт (1962). «§1-4: Определения и терминология». Графики потоков сигналов и приложения. Прентис Холл. п. 8. КАК В B0000CLM1G.
- ^ Дж. Р. Абрахамс; Дж. П. Коверли (2014). «Глава 2: Операции с потоковым графом». Анализ потока сигналов: Содружество и Международная библиотека. Эльзевир. стр.21 ff. ISBN 9781483180700.
- ^ Исаак М. Горовиц (2013). «Редукция сигнально-потоковых графиков». Синтез систем обратной связи. Эльзевир. стр.18 ff. ISBN 9781483267708.
- ^ (Огата 2002, стр.68, 106).
- ^ (Огата 2002, стр.105, 106).
- ^ а б (Хенли 1973, п. 12)
- ^ (Панг 2001, п. 37)
- ^ Примеры сокращения графа потока сигналов можно найти в (Робишо 1962, п. 186, п. 7-3 Алгебраическая редукция графов потоков сигналов)
- ^ а б (Робишо 1962, стр. 9–10, п. 1–5: Уменьшение потокового графика)
- ^ (Робишо 1962, pp. 182, 183 Sec. 7-1, 7-2 главы 7: Алгебраическая редукция графов потоков сигналов с помощью цифрового компьютера)
- ^ (Робишо 1962, п. 185, п. 7-2: Обобщение потоковых графов)
- ^ (Робишо 1962, стр.9, п. 1–5 УМЕНЬШЕНИЕ ГРАФИКА ПОТОКА)
- ^ Фахфах, Мурад; Тлело-Куаутле, Эстебан; В. Фернандес, Франсиско (2012). «Раздел 4.1.2 Алгебра графов потоков сигналов». В Фахфахе (ред.). Разработка аналоговых схем посредством символьного анализа. Издательство Bentham Science. п. 418. ISBN 978-1-60805-425-1.
- ^ Лабреш П., презентация: Линейные электрические цепи: анализ символьных сетей, 1977.
- ^ Карл Энгельман, Наследие MATHLAB 68, опубликовано в Proceeding SYMSAC '71 Протоколы второго симпозиума ACM по символическим и алгебраическим манипуляциям, стр. 29-41 [1]
- ^ «... решение совокупности одновременных линейных алгебраических уравнений. Эта проблема, обычно решаемая матричными методами, также может быть решена с помощью теории графов». Део, Нарсинг (1974). Теория графов с приложениями в инженерии и информатике. Прентис-Холл Индии. п. 416. ISBN 978-81-203-0145-0. также он-лайн на [2]
- ^ Део, Нарсинг (1974). Теория графов с приложениями в инженерии и информатике. Прентис-Холл Индии. п. 417. ISBN 978-81-203-0145-0. также он-лайн на [3]
- ^ "Граф потока сигналов можно рассматривать как упрощенную версию блок-схемы. ... для причин и следствий ... линейных систем ... мы можем рассматривать графы потоков сигналов как ограниченные более жесткими математическими правилами, тогда как использование обозначений блок-схемы менее строго ". Куо, Бенджамин С. (1991). Системы автоматического управления (6-е изд.). Прентис-Холл. п.77. ISBN 978-0-13-051046-4.
- ^ Джин Ф. Франклин; и другие. (29 апреля, 2014). «Приложение W.3 Уменьшение блок-схемы». Управление с обратной связью динамических систем. Прентис Холл.
- ^ В. У. Бакши У. А. Бакши (2007). «Таблица 5.6: Сравнение методов блок-схемы и графа потока сигналов». Техника управления. Технические публикации. п. 120. ISBN 9788184312935.
- ^ Ананд Кумар (2014). «Таблица: Сравнение блок-схемы и методов передачи сигналов». Системы управления (2-е изд.). PHI Learning Pvt. ООО п. 165. ISBN 9788120349391.
- ^ Х.А. Баркер; M Chen; П. Таунсенд (2014). «Алгоритмы преобразований между блок-схемами и цифровыми потоковыми графами». Компьютерное проектирование в системах управления 1988: избранные доклады 4-го симпозиума МФБ, Пекин, КНР, 23-25 августа 1988 г.. Эльзевир. стр.281 ff. ISBN 9781483298795.
- ^ Например, см. Артур Г.О. Мутамбара (1999). Проектирование и анализ систем управления. CRC Press. п. 238. ISBN 9780849318986.
- ^ Кацухико Огата (1997). «Графики прохождения сигналов». Современная контрольная техника (4-е изд.). Прентис Холл. п. 104. ISBN 978-0130432452.
- ^ Вольфганг Боруцкий (2009). Методология графа облигаций: разработка и анализ моделей мультидисциплинарных динамических систем. Springer Science & Business Media. п. 10. ISBN 9781848828827.
- ^ Джеймс Дж. Каллахан (2000). «Причинность: определение 2.10». Геометрия пространства-времени: введение в специальную и общую теорию относительности. Springer Science & Business Media. п. 76. ISBN 9780387986418.
- ^ Джон Дж. Х. Миллер; Роберт Вичневецкий (22–26 июля 1991 г.). Джон Дж. Х. Миллер; Роберт Вичневецкий (ред.). IMACS '91, Материалы 13-го Всемирного конгресса IMACS по вычислениям и прикладной математике: 22-26 июля 1991 г., Тринити-колледж, Дублин, Ирландия. Международная ассоциация математики и компьютеров в моделировании.
- ^ Франсуа Э. Селье; Эрнесто Кофман (2006). Непрерывное моделирование системы. Springer Science & Business Media. п. 15. ISBN 9780387261027.
- ^ См., Например, Стефан Левандовски; Саймон Фаррелл (2010). Вычислительное моделирование в познании: принципы и практика. Публикации SAGE. ISBN 9781452236193.
- ^ Дорф, Ричард С .; Епископ, Роберт Х. (2001). «Глава 2.-1: Введение» (PDF). Современные системы управления. Прентис Холл. п. 2. ISBN 978-0-13-030660-9.
- ^ Antao, B.A. A .; Бродерсен, А.Дж. (Июнь 1995 г.). «ARCHGEN: Автоматический синтез аналоговых систем». Транзакции IEEE в системах с очень крупномасштабной интеграцией (СБИС). 3 (2): 231–244. Дои:10.1109/92.386223.
- ^ Доболи, А .; Dhanwada, N .; Вемури, Р. (май 2000 г.). «Эвристический метод для генерации архитектуры системного уровня из представлений графа потока сигналов аналоговых систем». 2000 Международный симпозиум IEEE по схемам и системам. Новые технологии 21 века. Протоколы (IEEE Cat No. 00CH36353). Схемы и системы, 2000. Труды. ISCAS 2000 Женева. Международный симпозиум IEEE 2000 г. 3. С. 181–184. CiteSeerX 10.1.1.59.304. Дои:10.1109 / ISCAS.2000.856026. ISBN 978-0-7803-5482-1. S2CID 13948702.
- ^ а б c Хэпп, Уильям У. (1966). «Методы Flowgraph для замкнутых систем». IEEE Transactions по аэрокосмическим и электронным системам. АЕС-2 (3): 252–264. Bibcode:1966ITAES ... 2..252H. Дои:10.1109 / TAES.1966.4501761. S2CID 51651723.
- ^ а б c Поташ, Ханан; Макнейми, Лоуренс П. (1968). «Применение односторонних и графовых методов к анализу линейных цепей: Решение неитерационными методами». Труды Национальной конференции ACM: 367–378. Дои:10.1145/800186.810601. S2CID 16623657.
- ^ а б Окрент, Ховард; МакНами, Лоуренс П. (1970). "3. 3 Теория потокового графа" (PDF). Руководство пользователя и программиста NASAP-70. Лос-Анджелес, Калифорния: Школа инженерии и прикладных наук Калифорнийского университета в Лос-Анджелесе. С. 3–9.
- ^ Коу (1967, п. 57)
- ^ Арнальдо Д’Амико, Кристиан Фалькони, Джанлука Джустолизи, Гаэтано Палумбо (апрель 2007 года). «Сопротивление усилителей обратной связи: новое представление» (PDF). IEEE Transactions on Circuits and Systems - II Express Briefs. 54 (4): 298–302. CiteSeerX 10.1.1.694.8450. Дои:10.1109 / tcsii.2006.889713. S2CID 10154732.CS1 maint: несколько имен: список авторов (связь)
- ^ Пейнтер, Генри (1992). "Эпистемическая предыстория графов облигаций" (PDF): 10, 15 стр. Цитировать журнал требует
| журнал =(помощь) - ^ Houpis, Constantine H .; Шелдон, Стюарт Н. (2013). «раздел 8.8». Анализ и проектирование линейных систем управления с помощью MATLAB®, шестое издание. Бока-Ратон, Флорида: Пресса CRC. С. 171–172. ISBN 9781466504264.
- ^ Например: Baran, Thomas A .; Оппенхием, Алан В. (2011), "ОБРАЩЕНИЕ НЕЛИНЕЙНЫХ И ВРЕМЕННЫХ СИСТЕМ", 2011 г. Совещание по обучению цифровой обработке сигналов и обработке сигналов (DSP / SPE), Семинар по цифровой обработке сигналов и Образовательный семинар по обработке сигналов IEEE (DSP / SPE), IEEE, стр. 283–288, CiteSeerX 10.1.1.695.7460, Дои:10.1109 / DSP-SPE.2011.5739226, ISBN 978-1-61284-226-4, S2CID 5758954
- ^ а б Guilherme, J .; Horta, N.C .; Франка, Дж. Э. (1999). СИМВОЛИЧЕСКИЙ СИНТЕЗ НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАТЕЛЕЙ ДАННЫХ (PDF).
- ^ Холл, Джон Э. (2004-11-01). «Новаторское использование системного анализа для изучения регуляции сердечного выброса». Американский журнал физиологии. Регуляторная, интегративная и сравнительная физиология. 287 (5): R1009 – R1011. Дои:10.1152 / classicessays.00007.2004. ISSN 0363-6119. PMID 15475497.
Рисунок 2, компьютерная модель сердечно-сосудистой системы Артура Гайтона. скачать jpeg
- ^ BRZOZOWSKI, J.A .; МакКласки, Э. Дж. (1963). Методы построения графиков прохождения сигналов для последовательных диаграмм состояний цепей. Транзакции IEEE на электронных компьютерах. IEEE. п. 97.
- ^ Барри, Дж. Р., Ли, Э. А., и Мессершмитт, Д. Г. (2004). Цифровая связь (Третье изд.). Нью-Йорк: Спрингер. п. 86. ISBN 978-0-7923-7548-7.CS1 maint: несколько имен: список авторов (связь)
- ^ Хэпп, Уильям У. (1964). Гольдберг, М. Ф. (ред.). «Применение методов флоуграфа к решению проблем надежности». Физика отказа в электронике (AD434 / 329): 375–423. Дои:10.1109 / IRPS.1963.362257.
- ^ Холл, Джон Э. (23 августа 2004 г.). «Новаторское использование системного анализа для изучения регуляции сердечного выброса». Am J Physiol Regul Integr Comp Physiol. 287 (5): R1009 – R1011. Дои:10.1152 / classicessays.00007.2004. PMID 15475497.
- ^ (Робишо 1962, глава 5 Прямое моделирование на аналоговых компьютерах с помощью диаграмм прохождения сигналов)
Рекомендации
- Эрнест Дж. Хенли и Р. А. Уильямс (1973). Теория графов в современной технике; автоматизированное проектирование, управление, оптимизация, анализ надежности. Академическая пресса. ISBN 978-0-08-095607-7. Книга почти целиком посвящена этой теме.
- Коу, Бенджамин С. (1967), Системы автоматического управления, Прентис Холл
- Робишо, Луи П.А .; Морис Буазверт; Жан Роберт (1962). Графики потоков сигналов и приложения. Энглвуд Клиффс, Нью-Джерси: Prentice Hall. С. xiv, 214 с.
- Део, Нарсинг (1974), Теория графов с приложениями в инженерии и информатике, PHI Learning Pvt. Ltd., п. 418, г. ISBN 978-81-203-0145-0
- К. Туласирамен; MNS Swarmy (2011). «§6.11 Графы Коутса и Мейсона». Графики: теория и алгоритмы. Джон Вили и сыновья. стр.163 ff. ISBN 9781118030257.
- Огата, Кацухико (2002). «Раздел 3-9 Графики прохождения сигналов». Современная техника управления, 4-е издание. Прентис-Хэл. ISBN 978-0-13-043245-2.
- Панг, Хоман (2000-12-14). "2.5 Обзор графиков потоков сигналов" (PDF). Конструкция оптического предусилителя CMOS с использованием графического анализа цепей (Тезис). Кафедра электротехники и вычислительной техники, Университет Торонто. Проверить значения даты в:
| год = / | дата = несоответствие(помощь) © Авторское право Хоман Панг 2001
дальнейшее чтение
- Вай-Кай Чен (1976). Прикладная теория графов. Издательская компания Северной Голландии. ISBN 978-0720423624. Глава 3 посвящена основам, но приложения разбросаны по всей книге.
- Вай-Кай Чен (май 1964 г.). «Некоторые приложения линейных графиков». Контракт DA-28-043-AMC-00073 (E). Скоординированная научная лаборатория, Иллинойский университет, Урбана.
- К. Туласираман и М. Н. С. Свами (1992). Графики: теория и алгоритмы. 6.10-6.11 для основной математической идеи. ISBN 978-0-471-51356-8.
- Шу-Пак Чан (2006). «Теория графов». В Ричарде С. Дорфе (ред.). Цепи, сигналы и обработка речи и изображений (3-е изд.). CRC Press. § 3.6. ISBN 978-1-4200-0308-6. Сравнивает графовые подходы Мейсона и Коутса с подходом Максвелла с k-деревом.
- РФ Хоскинс (2014). «Блок-граф и сигнальный анализ линейных систем». В SR Deards (ред.). Последние разработки в теории сетей: материалы симпозиума, проведенного в Колледже аэронавтики, Крэнфилд, сентябрь 1961 г.. Эльзевир. ISBN 9781483223568. Сравнение полезности График Коутса и граф потока Мейсона.
внешняя ссылка
- М. Л. Эдвардс: S-параметры, графики потока сигналов и другие матричные представления Все права защищены
- Х Шмид: Графики прохождения сигналов в 12 коротких уроках
 Системы управления / схемы прохождения сигналов в Викиучебнике
Системы управления / схемы прохождения сигналов в Викиучебнике СМИ, связанные с Графики прохождения сигналов в Wikimedia Commons
СМИ, связанные с Графики прохождения сигналов в Wikimedia Commons







































