Модель асимптотического выигрыша - Asymptotic gain model
Эта статья нужны дополнительные цитаты для проверка. (Август 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В модель асимптотического выигрыша[1][2] (также известный как Метод Розенштарка[3]) является представлением выигрыша усилители отрицательной обратной связи задается соотношением асимптотического усиления:
куда это коэффициент возврата с отключенным источником входного сигнала (равным отрицательному значению усиление контура в случае одноконтурной системы, состоящей из односторонний блоки), грамм∞ - асимптотический выигрыш и грамм0 это термин прямой передачи. Эта форма для коэффициента усиления может обеспечить интуитивное понимание схемы, и ее часто легче получить, чем прямую атаку на коэффициент усиления.

На рисунке 1 показана блок-схема, которая приводит к выражению асимптотического усиления. Соотношение асимптотического усиления также может быть выражено как график потока сигналов. См. Рисунок 2. Модель асимптотического усиления - частный случай теорема о дополнительных элементах.

Определение терминов
Как непосредственно следует из предельных случаев выражения для коэффициента усиления, асимптотический коэффициент усиления грамм∞ это просто выигрыш системы, когда коэффициент возврата приближается к бесконечности:
в то время как срок прямой передачи грамм0 - выигрыш системы при нулевом коэффициенте доходности:
Преимущества
- Эта модель полезна, потому что она полностью характеризует усилители обратной связи, включая эффекты нагрузки и двусторонний свойства усилителей и сетей обратной связи.
- Часто усилители обратной связи проектируются таким образом, что коэффициент возврата Т намного больше единицы. В этом случае и при условии, что срок передачи прямой грамм0 мала (как это часто бывает), прирост грамм системы примерно равна асимптотическому усилению грамм∞.
- Асимптотический коэффициент усиления (обычно) зависит только от пассивных элементов в цепи и часто может быть обнаружен путем осмотра.
- Топологию обратной связи (последовательно-последовательно, последовательно-шунтирующую и т. Д.) Не нужно определять заранее, поскольку анализ во всех случаях одинаков.
Выполнение
Прямое применение модели включает следующие шаги:
- Выберите зависимый источник в цепи.
- Найди коэффициент возврата для этого источника.
- Найдите выигрыш грамм∞ непосредственно из схемы путем замены схемы на схему, соответствующую Т = ∞.
- Найдите выигрыш грамм0 непосредственно из схемы путем замены схемы на схему, соответствующую Т = 0.
- Подставьте значения для Т, Г∞ и грамм0 в формулу асимптотического усиления.
Эти шаги могут быть реализованы непосредственно в СПЕЦИЯ с использованием слабосигнальной схемы ручного анализа. При таком подходе легко доступны зависимые источники устройств. Напротив, для экспериментальных измерений с использованием реальных устройств или моделирования SPICE с использованием численно сгенерированных моделей устройств с недоступными зависимыми источниками для оценки коэффициента возврата требуется специальные методы.
Связь с классической теорией обратной связи
Классический теория обратной связи пренебрегает прямой связью (грамм0). Если прямая связь отброшена, выигрыш от модели асимптотического усиления становится
в то время как в классической теории обратной связи, с точки зрения коэффициента усиления без обратной связи А, коэффициент усиления с обратной связью (коэффициент усиления замкнутого контура) равен:
Сравнение двух выражений указывает на коэффициент обратной связи βFB является:
в то время как усиление разомкнутого контура:
Если точность достаточна (обычно это так), эти формулы предлагают альтернативную оценку Т: оценить коэффициент усиления без обратной связи и грамм∞ и используйте эти выражения, чтобы найти Т. Часто эти две оценки легче, чем оценка Т напрямую.
Примеры
Шаги по получению коэффициента усиления с использованием формулы асимптотического усиления описаны ниже для двух усилителей с отрицательной обратной связью. Пример с одним транзистором показывает, как этот метод работает в принципе для усилителя крутизны, а второй пример с двумя транзисторами показывает подход к более сложным случаям с использованием усилителя тока.
Одноступенчатый транзисторный усилитель

Рассмотрим простой FET усилитель обратной связи на рисунке 3. Цель состоит в том, чтобы найти низкочастотный, разомкнутый, транс-сопротивление усиление этой схемы грамм = vиз / яв с использованием модели асимптотического усиления.
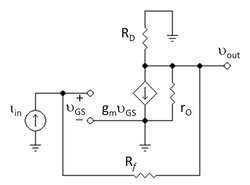

В слабосигнальный Эквивалентная схема показана на рисунке 4, где транзистор заменен на его гибридная пи модель.
Коэффициент возврата
Проще всего начать с определения коэффициента доходности. Т, потому что грамм0 и грамм∞ определяются как предельные формы усиления как Т стремится либо к нулю, либо к бесконечности. Чтобы выйти за эти пределы, необходимо знать, какие параметры Т зависит от. В этой схеме есть только один зависимый источник, поэтому в качестве отправной точки коэффициент возврата, связанный с этим источником, определяется, как указано в статье коэффициент возврата.
В коэффициент возврата находится с помощью рисунка 5. На рисунке 5 источник входного тока установлен на ноль. Путем отключения зависимого источника от выходной стороны схемы и короткого замыкания его клемм выходная сторона схемы изолирована от входной сигнал и цепь обратной связи нарушена. Тестовый ток ят заменяет зависимый источник. Затем определяется обратный ток, генерируемый в зависимом источнике испытательным током. Тогда коэффициент возврата равен Т = −яр / ят. Используя этот метод и заметив, что рD параллельно с рО, Т определяется как:
где приближение является точным в общем случае, когда рО >> рD. Из этих отношений ясно, что пределы Т → 0 или ∞, если положить крутизна граммм → 0 или ∞.[5]
Асимптотический выигрыш
Нахождение асимптотического выигрыша грамм∞ обеспечивает понимание и обычно может быть сделано путем осмотра. Найти грамм∞ мы позволяем граммм → ∞ и найдите полученное усиление. Ток стока, яD = граммм vGS, должно быть конечным. Следовательно, поскольку граммм приближается к бесконечности, vGS также должен приближаться к нулю. Поскольку источник заземлен, vGS = 0 означает vграмм = 0 тоже.[6] С vграмм = 0 и тот факт, что весь входной ток протекает через рж (поскольку полевой транзистор имеет бесконечное входное сопротивление), выходное напряжение просто -яв рж. Следовательно
Альтернативно грамм∞ - коэффициент усиления, найденный при замене транзистора идеальным усилителем с бесконечным коэффициентом усиления - a nullor.[7]
Прямой проход
Чтобы найти прямой проход мы просто позволяем граммм → 0 и вычислите полученное усиление. Токи через рж и параллельное сочетание рD || рО поэтому должны быть одинаковыми и равными яв. Таким образом, выходное напряжение яв (РD || рО).
Следовательно
где приближение является точным в общем случае, когда рО >> рD.
Общий выигрыш
Общая прирост сопротивления этого усилителя составляет:
Изучая это уравнение, представляется полезным сделать рD большой, чтобы общее усиление приближалось к асимптотическому усилению, что делает усиление нечувствительным к параметрам усилителя (граммм и рD). Кроме того, большой первый член снижает важность коэффициента прямого проникновения, который ухудшает характеристики усилителя. Один из способов увеличения рD заключается в замене этого резистора на активная нагрузка, например, текущее зеркало.

Двухкаскадный транзисторный усилитель
На рисунке 6 изображен двухтранзисторный усилитель с резистором обратной связи. рж. Этот усилитель часто называют обратная связь серии шунтов усилитель, и проанализирован на основе того, что резистор р2 идет последовательно с выходным током и выходным током выборки, а рж шунтируется (параллельно) входу и вычитает из входного тока. См. Статью о усилитель отрицательной обратной связи и ссылки Мейера или Седры.[8][9] То есть в усилителе используется обратная связь по току. Часто бывает неоднозначно, какой тип обратной связи используется в усилителе, и подход с асимптотическим коэффициентом усиления имеет то преимущество / недостаток, что он работает независимо от того, разбираетесь ли вы в схеме или нет.
На рисунке 6 показан выходной узел, но не указан выбор выходной переменной. В дальнейшем в качестве выходной переменной выбирается ток короткого замыкания усилителя, то есть ток коллектора выходного транзистора. Другие варианты вывода обсуждаются позже.
Для реализации модели асимптотического усиления можно использовать зависимый источник, связанный с любым транзистором. Здесь выбран первый транзистор.
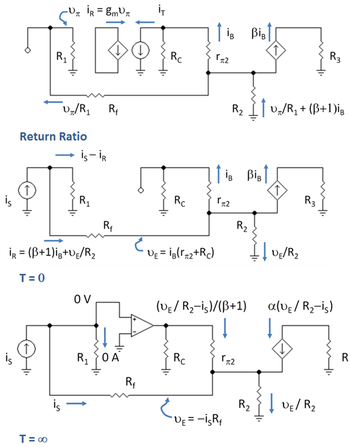
Коэффициент возврата
Схема для определения коэффициента возврата показана на верхней панели рисунка 7. Ярлыки показывают токи в различных ветвях, найденные с помощью комбинации Закон Ома и Законы Кирхгофа. Резистор р1 = RB // рπ1 и р3 = RC2 // РL. КВЛ с земли р1 на землю р2 обеспечивает:
KVL обеспечивает напряжение коллектора в верхней части рC в качестве
Наконец, KCL на этом сборщике обеспечивает
Подставляя первое уравнение во второе и второе в третье, коэффициент возврата находится как
Прирост грамм0 с T = 0
Схема для определения грамм0 показан на центральной панели рисунка 7. На рисунке 7 выходной переменной является выходной ток β.яB (ток нагрузки короткого замыкания), что приводит к усилению тока короткого замыкания усилителя, а именно βяB / яS:
С помощью Закон Ома, напряжение в верхней части р1 находится как
или, переставив термины,
Использование KCL в верхней части р2:
Напряжение эмиттера vE уже известно с точки зрения яB из диаграммы на рис. 7. Подставляя второе уравнение в первое, яB определяется с точки зрения яS один, и грамм0 становится:
Прирост грамм0 представляет собой прямую связь через сеть обратной связи и обычно незначительна.
Прирост грамм∞ с Т → ∞
Схема для определения грамм∞ показан на нижней панели рисунка 7. Введение в идеальный операционный усилитель (a nullor ) в этой схеме объясняется следующим образом. Когда Т → ∞, коэффициент усиления усилителя также стремится к бесконечности, и в этом случае дифференциальное напряжение, управляющее усилителем (напряжение на входном транзисторе рπ1) приводится к нулю и (согласно закону Ома при отсутствии напряжения) не потребляет входной ток. С другой стороны, выходной ток и выходное напряжение соответствуют требованиям схемы. Это поведение похоже на нульлор, поэтому можно ввести нульор для представления транзистора с бесконечным усилением.
Текущее усиление считывается непосредственно со схемы:
Сравнение с классической теорией обратной связи
В классической модели пренебрегают прямой связью и коэффициент обратной связи βFB (при условии, что транзистор β >> 1):
и коэффициент усиления без обратной связи А является:
Общий выигрыш
Приведенные выше выражения могут быть подставлены в уравнение модели асимптотического усиления, чтобы найти общий коэффициент усиления G. Текущий коэффициент усиления усилителя при короткозамкнутой нагрузке.
Прибыль с использованием альтернативных выходных переменных
В усилителе на Рисунке 6 рL и рC2 параллельны. Чтобы получить усиление сопротивления, скажем, Аρ, то есть коэффициент усиления с использованием напряжения в качестве выходной переменной, коэффициент усиления по току короткого замыкания грамм умножается на рC2 // РL в соответствии с Закон Ома:
В разомкнутая цепь коэффициент усиления по напряжению определяется из Аρ установив рL → ∞.
Чтобы получить коэффициент усиления по току при токе нагрузки яL в нагрузочном резисторе рL это выходная переменная, скажем Ая, формула для текущее деление используется: яL = яиз × RC2 / ( РC2 + RL ) и коэффициент усиления тока короткого замыкания грамм умножается на это коэффициент загрузки:
Конечно, усиление тока короткого замыкания восстанавливается установкой рL = 0 Ом.
Ссылки и примечания
- ^ Миддлбрук, РД: Конструктивный анализ усилителей обратной связи; Proc. Национальной конференции по электронике, Vol. XX, октябрь 1964 г., стр. 1–4.
- ^ Розенстарк, Сол (1986). Принципы усилителя обратной связи. Нью-Йорк: Кольер Макмиллан. п. 15. ISBN 0-02-947810-3.
- ^ Палумбо, Гаэтано и Сальваторе Пенниси (2002). Усилители обратной связи: теория и конструкция. Бостон / Дордрехт / Лондон: Kluwer Academic. С. §3.3 с. 69–72. ISBN 0-7923-7643-9.
- ^ Пол Р. Грей, Херст П. Дж. Льюис С. Х. и Мейер Р. Г. (2001). Анализ и проектирование аналоговых интегральных схем (Четвертое изд.). Нью-Йорк: Вили. Рисунок 8.42 с. 604. ISBN 0-471-32168-0.
- ^ Хотя меняется рD // рО также может привести к ограничению коэффициента возврата, эти значения резистора влияют и на другие аспекты схемы. Это параметр управления зависимого источника, который необходимо варьировать, поскольку он влияет на Только зависимый источник.
- ^ Поскольку входное напряжение vGS приближается к нулю, когда коэффициент возврата увеличивается, входной импеданс усилителя также стремится к нулю, что, в свою очередь, означает (из-за текущее деление ), что усилитель работает лучше всего, если входным сигналом является ток. Если используется источник Norton, а не идеальный источник тока, формальные уравнения, полученные для Т будет таким же, как и для источника напряжения Thévenin. Обратите внимание, что в случае входного тока, грамм∞ это транс-сопротивление прирост.
- ^ Верхувен CJ, ван Ставерен A, Monna GL, Kouwenhoven MH, Yildiz E (2003). Структурированная электроника: усилители с отрицательной обратной связью. Бостон / Дордрехт / Лондон: Kluwer Academic. С. §2.3 - §2.5 с. 34–40. ISBN 1-4020-7590-1.
- ^ P R Серый; П. Дж. Херст; С. Х. Льюис и Р. Г. Мейер (2001). Анализ и проектирование аналоговых интегральных схем (Четвертое изд.). Нью-Йорк: Вили. С. 586–587. ISBN 0-471-32168-0.
- ^ А.С. Седра и К.С. Смит (2004). Микроэлектронные схемы (Пятое изд.). Нью-Йорк: Оксфорд. Пример 8.4, стр. 825–829 и моделирование PSpice, стр. 855–859. ISBN 0-19-514251-9.
Смотрите также
- Теорема Блэкмана
- Теорема о дополнительных элементах
- Формула усиления Мейсона
- Усилители обратной связи
- Коэффициент возврата
- График потока сигналов























![G_0 = frac { beta} {
( beta +1) left (1 + frac {R_f} {R_1} right) + (r_ { pi 2} + R_C) left [ frac {1} {R_1} + frac {1} {R_2} left (1 + frac {R_f} {R_1} right) right]
}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1f13047df4e6e46b0cb202e1f3fc3b18ea86dfc)




