Каталонский треугольник - Википедия - Catalans triangle

В комбинаторная математика, Каталонский треугольник это числовой треугольник чьи записи ${ Displaystyle С (п, к)}$ укажите количество строк, состоящих из п Х и k Y такое, что ни один начальный сегмент строки не имеет больше Y, чем X. Это обобщение Каталонские числа, и назван в честь Эжен Шарль Каталан. Бейли^[1] показывает, что ${ Displaystyle С (п, к)}$ удовлетворяют следующим свойствам:

${ Displaystyle С (п, 0) = 1 { текст {for}} п geq 0}$ .
${ Displaystyle С (п, 1) = п { текст {для}} п geq 1}$ .
${ Displaystyle С (п + 1, к) = С (п + 1, к-1) + С (п, к) { текст {для}} 1 <к <п + 1}$
${ Displaystyle С (п + 1, п + 1) = С (п + 1, п) { текст {для}} п geq 1}$ .

Формула 3 показывает, что вход в треугольник получается рекурсивно путем добавления чисел слева и сверху в треугольнике. Самое раннее появление каталонского треугольника вместе с формулой рекурсии находится на странице 214 трактата по исчислению, опубликованного в 1800 году.^[2] к Луи Франсуа Антуан Арбогаст.

Шапиро^[3] вводит еще один треугольник, который он называет каталонским треугольником, отличный от обсуждаемого здесь.

Общая формула

Общая формула для ${ Displaystyle С (п, к)}$ дан кем-то^[1]^[4]

{ Displaystyle С (п, к) = { гидроразрыва {(п + к)! (п-к + 1)} {к! (п + 1)!}},}

куда $п$ и $k$ неотрицательные целые числа и $п!$ обозначает факториал. Таким образом, для $k$ >0, ${ displaystyle C (n, k) = left ({ begin {array} {c} n + k k end {array}} right) - left ({ begin {array} {c} n + k k-1 end {array}} right)}$ .

Диагональ $C (п, п)$ это $п$ -го Каталонский номер. Сумма строки $п$ -я строка - это $(п + 1)$ -го Каталонский номер.

Некоторые значения даны^[5]

k п	0	1	2	3	4	5	6	7	8
0	1
1	1	1
2	1	2	2
3	1	3	5	5
4	1	4	9	14	14
5	1	5	14	28	42	42
6	1	6	20	48	90	132	132
7	1	7	27	75	165	297	429	429
8	1	8	35	110	275	572	1001	1430	1430

Обобщение

Каталонские трапеции представляют собой счетный набор числовых трапеций, образующих каталонский треугольник. Каталонская трапеция порядка $м = 1, 2, 3, ...$ числовая трапеция, элементы которой ${ Displaystyle C_ {m} (п, к)}$ укажите количество строк, состоящих из $п$ Икс и $k$ Y-s такие, что в каждом начальном сегменте строки количество Y-s не превышает количества X-ов на $м$ или больше.^[6] По определению, каталонская трапеция порядка $м = 1$ каталонский треугольник, т.е. ${ Displaystyle C_ {1} (п, к) = С (п, к)}$ .

Некоторые ценности каталонской трапеции порядка $м = 2$ даны

k п	0	1	2	3	4	5	6	7	8
0	1	1
1	1	2	2
2	1	3	5	5
3	1	4	9	14	14
4	1	5	14	28	42	42
5	1	6	20	48	90	132	132
6	1	7	27	75	165	297	429	429
7	1	8	35	110	275	572	1001	1430	1430

Некоторые ценности каталонской трапеции порядка $м = 3$ даны

k п	0	1	2	3	4	5	6	7	8	9
0	1	1	1
1	1	2	3	3
2	1	3	6	9	9
3	1	4	10	19	28	28
4	1	5	15	34	62	90	90
5	1	6	21	55	117	207	297	297
6	1	7	28	83	200	407	704	1001	1001
7	1	8	36	119	319	726	1430	2431	3432	3432

Опять же, каждый элемент - это сумма элемента выше и элемента слева.

Общая формула для ${ Displaystyle C_ {m} (п, к)}$ дан кем-то

{ displaystyle C_ {m} (n, k) = { begin {case} left ({ begin {array} {c} n + k k end {array}} right) & , , , 0 leq k n + m-1 end {case}}}

( $п = 0, 1, 2, ...$ , $k = 0, 1, 2, ...$ , $м = 1, 2, 3, ...$ ).

Доказательства общей формулы для ${ Displaystyle C_ {m} (п, к)}$

Доказательство 1

Это доказательство включает расширение метода отражений Андреса, который использовался во втором доказательстве для Каталонский номер. Ниже показано, как каждый путь снизу слева ${ displaystyle (0,0)}$ вверху справа ${ Displaystyle (к, п)}$ диаграммы, которая пересекает ограничение ${ Displaystyle п-к + м-1 = 0}$ также можно отразить до конечной точки ${ Displaystyle (п + м, к-м)}$ .

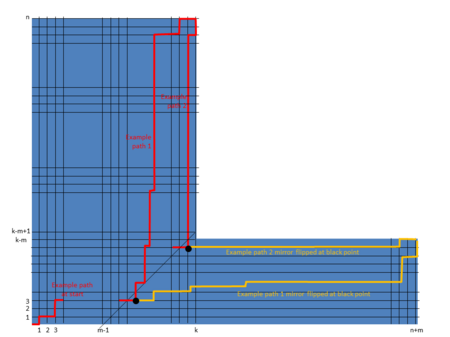
Рассмотрим три случая, чтобы определить количество путей из ${ displaystyle (0,0)}$ к ${ Displaystyle (к, п)}$ которые не выходят за рамки ограничения:

(1) когда ${ displaystyle m> k}$ ограничение не может быть пересечено, поэтому все пути от ${ displaystyle (0,0)}$ к ${ Displaystyle (к, п)}$ действительны, т.е. ${ displaystyle C_ {m} (n, k) = left ({ begin {array} {c} n + k k end {array}} right)}$ .

(2) когда ${ Displaystyle к-м + 1> п}$ невозможно сформировать путь, который не пересекает ограничение, т.е. ${ Displaystyle C_ {m} (п, к) = 0}$ .

(3) когда ${ Displaystyle м Leq К Leq п + м-1}$ , тогда ${ Displaystyle C_ {m} (п, к)}$ количество "красных" путей ${ displaystyle left ({ begin {array} {c} n + k k end {array}} right)}$ минус количество "желтых" путей, которые пересекают ограничение, т.е. ${ displaystyle left ({ begin {array} {c} (n + m) + (km) km end {array}} right) = left ({ begin {array} {c} n + k km end {array}} right)}$ .

Таким образом, количество путей от ${ displaystyle (0,0)}$ к ${ Displaystyle (к, п)}$ которые не выходят за рамки ограничений ${ Displaystyle п-к + м-1 = 0}$ как указано в формуле в предыдущем разделе "Обобщение".

Доказательство 2

Во-первых, мы подтверждаем справедливость рекуррентного соотношения ${ Displaystyle C_ {m} (n, k) = C_ {m} (n-1, k) + C_ {m} (n, k-1)}$ разрушая ${ Displaystyle C_ {m} (п, к)}$ на две части, первая для комбинаций XY, оканчивающихся на X, а вторая для тех, которые заканчиваются на Y. Таким образом, первая группа имеет ${ Displaystyle C_ {m} (п-1, к)}$ допустимые комбинации, а второй ${ Displaystyle C_ {m} (п, k-1)}$ . Доказательство 2 завершается проверкой того, что решение удовлетворяет рекуррентному соотношению и подчиняется начальным условиям для ${ Displaystyle C_ {m} (п, 0)}$ и ${ displaystyle C_ {m} (0, k)}$ .