Алгоритм Чанса - Википедия - Chans algorithm

Двухмерная демонстрация алгоритма Чана. Однако обратите внимание, что алгоритм делит точки произвольно, а не по x-координате.

В вычислительная геометрия, Алгоритм Чана,^[1] названный в честь Тимоти М. Чан, является оптимальным алгоритм, чувствительный к выходу вычислить выпуклый корпус набора ${ displaystyle P}$ из ${ displaystyle n}$ точек в 2- или 3-мерном пространстве. Алгоритм принимает ${ Displaystyle О (п лог ч)}$ время, где ${ displaystyle h}$ - количество вершин выхода (выпуклой оболочки). В плоском случае алгоритм объединяет ${ Displaystyle О (п журнал п)}$ алгоритм (Сканирование Грэма, например) с Марш Джарвиса (${ Displaystyle О (нх)}$), чтобы получить оптимальную ${ Displaystyle О (п лог ч)}$ время. Алгоритм Чана примечателен тем, что он намного проще, чем Алгоритм Киркпатрика – Зейделя, и естественно распространяется на трехмерное пространство. Эта парадигма^[2] был независимо разработан Фрэнком Нильсеном в его докторской диссертации. Тезис.^[3]

Алгоритм

Обзор

Для одного прохода алгоритма требуется параметр ${ displaystyle m}$ который находится между 0 и ${ displaystyle n}$ (количество точек нашего набора ${ displaystyle P}$). В идеале, ${ displaystyle m = h}$ но ${ displaystyle h}$число вершин в выходной выпуклой оболочке изначально неизвестно. Несколько проходов с увеличением значений ${ displaystyle m}$ выполняются, которые затем прекращаются, когда ${ displaystyle m geq h}$(см. ниже о выборе параметра ${ displaystyle m}$).

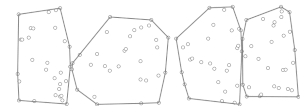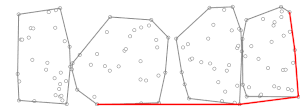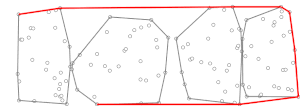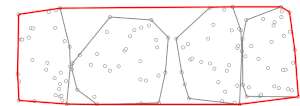
Алгоритм начинается с произвольного разбиения множества точек ${ displaystyle P}$ в ${ Displaystyle К = lceil п / м rceil}$ подмножества ${ displaystyle (Q_ {k}) _ {k = 1,2, ... K}}$ максимум с ${ displaystyle m}$ очки каждый; Заметь ${ Displaystyle К = О (п / м)}$.

Для каждого подмножества ${ displaystyle Q_ {k}}$, он вычисляет выпуклую оболочку, ${ displaystyle C_ {k}}$, используя ${ Displaystyle О (п журнал р)}$ алгоритм (например, Сканирование Грэма ), куда ${ displaystyle p}$ - количество точек в подмножестве. Поскольку есть ${ displaystyle K}$ подмножества ${ Displaystyle О (м)}$ очков каждый, эта фаза занимает ${ Displaystyle К CDOT О (м журнал м) = О (п журнал м)}$ время.

На втором этапе Марш Джарвиса выполняется с использованием предварительно вычисленных (мини) выпуклых оболочек, ${ displaystyle (C_ {k}) _ {k = 1,2, ... K}}$. На каждом шаге алгоритма марша Джарвиса у нас есть точка ${ displaystyle p_ {i}}$ в выпуклой оболочке (вначале ${ displaystyle p_ {i}}$ может быть дело в ${ displaystyle P}$ с наименьшей координатой y, которая гарантированно находится в выпуклой оболочке ${ displaystyle P}$), и нужно найти точку ${ Displaystyle р_ {я + 1} = е (р_ {я}, Р)}$ так что все остальные точки ${ displaystyle P}$ находятся справа от линии ${ Displaystyle р_ {я} р_ {я + 1}}$^{[требуется разъяснение ]}, где обозначение ${ Displaystyle р_ {я + 1} = е (р_ {я}, Р)}$ просто означает, что следующая точка, то есть ${ displaystyle p_ {я + 1}}$, определяется как функция ${ displaystyle p_ {i}}$ и ${ displaystyle P}$. Выпуклая оболочка множества ${ displaystyle Q_ {k}}$, ${ displaystyle C_ {k}}$, известен и содержит не более ${ displaystyle m}$ точек (перечисленных в порядке по часовой стрелке или против часовой стрелки), что позволяет вычислить ${ displaystyle f (p_ {i}, Q_ {k})}$ в ${ Displaystyle О ( журнал м)}$ время по бинарный поиск^{[как? ]}. Следовательно, вычисление ${ displaystyle f (p_ {i}, Q_ {k})}$ для всех ${ displaystyle K}$ подмножества могут быть выполнены в ${ Displaystyle О (К журнал м)}$ время. Тогда мы можем определить ${ displaystyle f (p_ {i}, P)}$ используя ту же технику, что обычно используется в марше Джарвиса, но только с учетом очков ${ Displaystyle (е (п_ {я}, Q_ {к})) _ {1 leq k leq K}}$ (т.е. точки в выпуклой мини-оболочке) вместо всего множества ${ displaystyle P}$. По этим пунктам одна итерация марша Джарвиса ${ Displaystyle О (К)}$ что незначительно по сравнению с вычислением для всех подмножеств. Марш Джарвиса завершается, когда процесс повторяется. ${ Displaystyle О (ч)}$ раз (потому что, как работает марш Джарвиса, самое большее после ${ displaystyle h}$ итераций его самого внешнего цикла, где ${ displaystyle h}$ - количество точек в выпуклой оболочке ${ displaystyle P}$, мы должны были найти выпуклую оболочку), поэтому вторая фаза принимает ${ Displaystyle О (кх log м)}$ время, эквивалентное ${ Displaystyle О (п лог ч)}$ время, если ${ displaystyle m}$ близко к ${ displaystyle h}$ (см. ниже описание стратегии выбора ${ displaystyle m}$ так что это так).

Выполняя две описанные выше фазы, выпуклая оболочка ${ displaystyle n}$ баллы рассчитываются в ${ Displaystyle О (п лог ч)}$ время.

Выбор параметра ${ displaystyle m}$

Если выбрано произвольное значение для ${ displaystyle m}$, может случиться так, что ${ displaystyle m$. В этом случае после ${ displaystyle m}$ шаги второй фазы, мы прерываем Марш Джарвиса поскольку доведение до конца заняло бы слишком много времени. ${ Displaystyle О (п журнал м)}$ время будет потрачено, а выпуклая оболочка не будет рассчитана.

Идея состоит в том, чтобы выполнить несколько проходов алгоритма с увеличением значений ${ displaystyle m}$; каждый проход завершается (успешно или безуспешно) в ${ Displaystyle О (п журнал м)}$ время. Если ${ displaystyle m}$ слишком медленно увеличивается между проходами, количество итераций может быть большим; с другой стороны, если он поднимается слишком быстро, первый ${ displaystyle m}$ для которых алгоритм завершается успешно, может быть намного больше, чем ${ displaystyle h}$, и создать сложность ${ Displaystyle О (п журнал м)> О (п журнал ч)}$.

Стратегия квадрата

Одна из возможных стратегий - квадрат значение ${ displaystyle m}$ на каждой итерации до максимального значения ${ displaystyle n}$ (соответствует разделу в синглетонах).^[4] Начиная со значения 2 на итерации ${ displaystyle t}$, ${ Displaystyle м = мин влево (п, 2 ^ {2 ^ {t}} вправо)}$ выбран. В таком случае, ${ Displaystyle О ( журнал журнал ч)}$ итерации выполняются, учитывая, что алгоритм завершается, как только мы

${ Displaystyle м = 2 ^ {2 ^ {t}} geq h iff log left (2 ^ {2 ^ {t}} right) geq log h iff 2 ^ {t} geq log h iff log {2 ^ {t}} geq log { log h} iff t geq log { log h},}$

с логарифмом по основанию ${ displaystyle 2}$, а общее время работы алгоритма равно

${ displaystyle sum _ {t = 0} ^ { lceil log log h rceil} O left (п log left (2 ^ {2 ^ {t}} right) right) = O (n) sum _ {t = 0} ^ { lceil log log h rceil} O (2 ^ {t}) = O left (n cdot 2 ^ {1+ lceil log log h rceil} right) = O (n log h).}$

В трех измерениях

Чтобы обобщить эту конструкцию на трехмерный случай, ${ Displaystyle О (п журнал п)}$ Алгоритм для вычисления трехмерной выпуклой оболочки по Препарате и Хонгу должен использоваться вместо сканирования Грэма, а также необходимо использовать трехмерную версию марша Джарвиса. Временная сложность остается ${ Displaystyle О (п лог ч)}$.^[1]

Псевдокод

В следующем псевдокоде текст между скобками и курсивом является комментарием. Чтобы полностью понять следующий псевдокод, рекомендуется, чтобы читатель уже был знаком с Сканирование Грэма и Марш Джарвиса алгоритмы вычисления выпуклой оболочки, ${ displaystyle C}$, множества точек,${ displaystyle P}$.

Вход: Набор ${ displaystyle P}$ с ${ displaystyle n}$ точки .

Выход: Набор ${ displaystyle C}$ с ${ displaystyle h}$ точек, выпуклая оболочка ${ displaystyle P}$.

(Выберите точку ${ displaystyle P}$ который гарантированно находится в ${ displaystyle C}$: например, точка с самой низкой координатой y.)

(Эта операция занимает ${ Displaystyle { mathcal {O}} (п)}$ время: например, мы можем просто перебрать ${ displaystyle P}$.)

${ displaystyle p_ {1}: = ВЫБРАТЬ _START (P)}$

(${ displaystyle p_ {0}}$ используется в марше Джарвиса этого алгоритма Чана,

чтобы вычислить вторую точку, ${ displaystyle p_ {2}}$, в выпуклой оболочке ${ displaystyle P}$.)

(Примечание: ${ displaystyle p_ {0}}$ является нет точка ${ displaystyle P}$.)

(Для получения дополнительной информации см. Комментарии рядом с соответствующей частью алгоритма Чана.)

${ displaystyle p_ {0}: = (- infty, 0)}$

(Примечание: ${ displaystyle h}$, количество точек в конечной выпуклой оболочке ${ displaystyle P}$, является нет известен.)

(Это итерации, необходимые для определения ценности ${ displaystyle m}$, что является оценкой ${ displaystyle h}$.)

(${ displaystyle h leq m}$ требуется, чтобы алгоритм Чана находил выпуклую оболочку ${ displaystyle P}$.)

(Более конкретно, мы хотим ${ Displaystyle ч Leq м Leq ч ^ {2}}$, чтобы не выполнять слишком много ненужных итераций

и так что временная сложность этого алгоритма Чана равна ${ Displaystyle { mathcal {O}} (п log ч)}$.)

(Как объяснялось выше в этой статье, мы используем стратегию, в которой не более ${ Displaystyle журнал журнал п}$ итерации необходимы, чтобы найти ${ displaystyle m}$.)

(Примечание: финальный ${ displaystyle m}$ не может быть равно ${ displaystyle h}$, но никогда не меньше чем ${ displaystyle h}$ и больше чем ${ displaystyle h ^ {2}}$.)

(Тем не менее, этот алгоритм Чана останавливается однажды ${ displaystyle h}$ выполняются итерации самого внешнего цикла,

то есть, даже если ${ displaystyle m neq h}$, это не работает ${ displaystyle m}$ итераций самого внешнего цикла.)

(Для получения дополнительной информации см. Часть марша Джарвиса этого алгоритма ниже, где ${ displaystyle C}$ возвращается, если ${ displaystyle p_ {я + 1} == p_ {1}}$.)

за ${ Displaystyle 1 Leq T Leq журнал журнал п}$ делать

(Установить параметр ${ displaystyle m}$ для текущей итерации. Мы используем «схему возведения в квадрат», как описано выше в этой статье.

Есть и другие схемы: например, «схема удвоения», где ${ displaystyle m = 2 ^ {t}}$, за ${ Displaystyle Т = 1, точки, влево lceil log ч вправо rceil}$.

Однако, если мы воспользуемся «схемой удвоения», итоговая временная сложность этого алгоритма Чана составит ${ Displaystyle { mathcal {O}} (п журнал ^ {2} ч)}$.)

${ displaystyle m: = 2 ^ {2 ^ {t}}}$

(Инициализируйте пустой список (или массив) для хранения точек выпуклой оболочки ${ displaystyle P}$, как они найдены.)

${ Displaystyle C: = ()}$

${ displaystyle ADD (C, p_ {1})}$

(Произвольно разделить набор точек ${ displaystyle P}$ в ${ displaystyle K = left lceil { frac {n} {m}} right rceil}$ подмножества примерно ${ displaystyle m}$ элементов каждый.)

${ displaystyle Q_ {1}, Q_ {2}, dots, Q_ {K}: = SPLIT (P, m)}$

(Вычислите выпуклую оболочку всех ${ displaystyle K}$ подмножества точек, ${ displaystyle Q_ {1}, Q_ {2}, dots, Q_ {K}}$.)

(Занимает ${ Displaystyle { mathcal {O}} (км log м) = { mathcal {O}} (п log м)}$ время.)

Если ${ displaystyle m leq h ^ {2}}$, то временная сложность равна ${ displaystyle { mathcal {O}} (п log h ^ {2}) = { mathcal {O}} (n log h)}$.)

за ${ Displaystyle 1 Leq K Leq K}$ делать

(Вычислить выпуклую оболочку подмножества ${ displaystyle k}$, ${ displaystyle Q_ {k}}$, используя сканирование Грэма, которое берет ${ Displaystyle { mathcal {O}} (м журнал м)}$ время.)

(${ displaystyle C_ {k}}$ - выпуклая оболочка множества точек ${ displaystyle Q_ {k}}$.)

${ displaystyle C_ {k}: = GRAHAM _SCAN (Q_ {k})}$

(Здесь выпуклые оболочки ${ displaystyle C_ {1}, C_ {2}, dots, C_ {K}}$ соответственно подмножеств точек ${ displaystyle Q_ {1}, Q_ {2}, dots, Q_ {K}}$ были вычислены.)

(Теперь используйте модифицированная версия из Марш Джарвиса алгоритм вычисления выпуклой оболочки ${ displaystyle P}$.)

(Марш Джарвиса выступает в ${ Displaystyle { mathcal {O}} (нч)}$ время, где ${ displaystyle n}$ количество входных точек и ${ displaystyle h}$ - количество точек в выпуклой оболочке.)

(Учитывая, что марш Джарвиса - это алгоритм, чувствительный к выходу время его работы зависит от размеров выпуклой оболочки, ${ displaystyle h}$.)

(На практике это означает, что марш Джарвиса выполняет ${ displaystyle h}$ итерации самого внешнего цикла.

На каждой из этих итераций он выполняет не более ${ displaystyle n}$ итераций его самого внутреннего цикла.)

(Мы хотим ${ Displaystyle ч Leq м Leq ч ^ {2}}$, поэтому мы не хотим выполнять больше, чем ${ displaystyle m}$ итераций в следующем внешнем цикле.)

(Если наш текущий ${ displaystyle m}$ меньше чем ${ displaystyle h}$, т.е. ${ displaystyle m$выпуклая оболочка ${ displaystyle P}$ Не может быть найдено.)

(В этой модифицированной версии марша Джарвиса мы выполняем операцию внутри самого внутреннего цикла, который принимает ${ Displaystyle { mathcal {O}} ( log м)}$ время.

Следовательно, общая временная сложность этой модифицированной версии составляет

${ displaystyle { mathcal {O}} (mK log m) = { mathcal {O}} (m left lceil { frac {n} {m}} right rceil log m) = { mathcal {O}} (n log m) = { mathcal {O}} (n log 2 ^ {2 ^ {t}}) = { mathcal {O}} (n2 ^ {t}). }$

Если ${ displaystyle m leq h ^ {2}}$, то временная сложность равна ${ displaystyle { mathcal {O}} (п log h ^ {2}) = { mathcal {O}} (n log h)}$.)

за ${ Displaystyle 1 Leq я Leq м}$ делать

(Примечание: здесь точка в выпуклой оболочке ${ displaystyle P}$ уже известно, то есть ${ displaystyle p_ {1}}$.)

(В этом внутреннем за петля, ${ displaystyle K}$ возможные следующие точки на выпуклой оболочке ${ displaystyle P}$, ${ Displaystyle q_ {я, 1}, q_ {я, 2}, точки, q_ {я, K}}$, вычисляются.)

(Каждый из них ${ displaystyle K}$ возможные следующие точки взяты из другого ${ displaystyle C_ {k}}$:

то есть, ${ displaystyle q_ {i, k}}$ возможная следующая точка на выпуклой оболочке ${ displaystyle P}$ который является частью выпуклой оболочки ${ displaystyle C_ {k}}$.)

(Примечание: ${ Displaystyle q_ {я, 1}, q_ {я, 2}, точки, q_ {я, K}}$ зависит от ${ displaystyle i}$: то есть для каждой итерации ${ displaystyle i}$, у нас есть ${ displaystyle K}$ возможные следующие точки на выпуклой оболочке ${ displaystyle P}$.)

(Примечание: на каждой итерации ${ displaystyle i}$, только одна из точек среди ${ Displaystyle q_ {я, 1}, q_ {я, 2}, точки, q_ {я, K}}$ добавляется к выпуклой оболочке ${ displaystyle P}$.)

за ${ Displaystyle 1 Leq K Leq K}$ делать

(${ displaystyle JARVIS _BINARY _SEARCH}$ находит точку ${ displaystyle d in C_ {k}}$ такой, что угол ${ Displaystyle измеренный угол p_ {i-1} p_ {i} d}$ максимально^{[Почему? ]},

куда ${ Displaystyle измеренный угол p_ {i-1} p_ {i} d}$ угол между векторами ${ displaystyle { overrightarrow {p_ {i} p_ {i-1}}}}$ и ${ displaystyle { overrightarrow {p_ {i} d}}}$. Такой ${ displaystyle d}$ хранится в ${ displaystyle q_ {i, k}}$.)

(Углы вычислять напрямую не требуется: ориентационный тест может быть использован^{[как? ]}.)

(${ displaystyle JARVIS _BINARY _SEARCH}$ может быть выполнено в ${ Displaystyle { mathcal {O}} ( log м)}$ время^{[как? ]}.)

(Примечание: на итерации ${ displaystyle i = 1}$, ${ Displaystyle р_ {я-1} = р_ {0} = (- infty, 0)}$ и ${ displaystyle p_ {1}}$ известна и является точкой в ​​выпуклой оболочке ${ displaystyle P}$:

в данном случае это точка ${ displaystyle P}$ с самой низкой координатой y.)

${ displaystyle q_ {i, k}: = JARVIS _BINARY _SEARCH (p_ {i-1}, p_ {i}, C_ {k})}$

(Выберите точку ${ Displaystyle г в {q_ {я, 1}, q_ {я, 2}, точки, q_ {я, К} }}$ который максимизирует угол ${ Displaystyle измеренный угол p_ {i-1} p_ {i} z}$^{[Почему? ]} быть следующей точкой на выпуклой оболочке ${ displaystyle P}$.)

${ displaystyle p_ {i + 1}: = JARVIS _NEXT _CH _POINT (p_ {i-1}, p_ {i}, (q_ {i, 1}, q_ {i, 2}, dots, q_ {i, K}))}$

(Марш Джарвиса заканчивается, когда следующая выбранная точка на выпуклой оболочке, ${ displaystyle p_ {я + 1}}$, - начальная точка, ${ displaystyle p_ {1}}$.)

если ${ displaystyle p_ {я + 1} == p_ {1}}$

(Верните выпуклую оболочку ${ displaystyle P}$ который содержит ${ displaystyle i = h}$ точки.)

(Примечание: конечно, возвращать не нужно ${ displaystyle p_ {я + 1}}$ что равно ${ displaystyle p_ {1}}$.)

возвращаться ${ Displaystyle C: = (p_ {1}, p_ {2}, dots, p_ {i})}$

еще

${ displaystyle ADD (C, p_ {я + 1})}$

(Если после ${ displaystyle m}$ итераций точка ${ displaystyle p_ {я + 1}}$ не был найден так что ${ displaystyle p_ {я + 1} == p_ {1}}$, тогда ${ displaystyle m$.)

(Нам нужно начать с более высокого значения для ${ displaystyle m}$.)

Выполнение

В статье Чана содержится несколько предложений, которые могут улучшить практическую производительность алгоритма, например:

• При вычислении выпуклой оболочки подмножества исключите точки, которые не находятся в выпуклой оболочке, из рассмотрения в последующих выполнениях.
• Выпуклые оболочки более крупных наборов точек могут быть получены путем объединения ранее вычисленных выпуклых оболочек вместо пересчета с нуля.
• В соответствии с вышеизложенной идеей основная стоимость алгоритма заключается в предварительной обработке, то есть вычислении выпуклой оболочки групп. Чтобы снизить эту стоимость, мы можем рассмотреть возможность повторного использования корпусов, вычисленных на предыдущей итерации, и их объединения по мере увеличения размера группы.

Расширения

Статья Чана содержит некоторые другие проблемы, известные алгоритмы которых можно сделать оптимально чувствительными к выходным данным, используя его технику, например:

• Вычисление нижнего конверта ${ Displaystyle L (S)}$ набора ${ displaystyle S}$ из ${ displaystyle n}$ отрезки прямой, который определяется как нижняя граница неограниченного трапеция из образованных перекрестками.
• Hershberger^[5] дал ${ Displaystyle О (п журнал п)}$ алгоритм, который можно ускорить до ${ Displaystyle О (п лог ч)}$, где h - количество ребер в конверте

• Построение алгоритмов, чувствительных к выходу, для выпуклых оболочек больших размеров. Используя точки группировки и эффективные структуры данных, ${ Displaystyle О (п лог ч)}$ сложность может быть достигнута при условии, что h имеет полиномиальный порядок от ${ displaystyle n}$.

Смотрите также

• Алгоритмы выпуклой оболочки

Рекомендации