Упаковка круга в квадрат - Circle packing in a square
Упаковка круга в квадрат это проблема упаковки в прикладной математика, где цель - упаковать п единичные круги в наименьшее возможное квадрат; или, что то же самое, организовать п точки в единичном квадрате, стремящиеся получить наибольшее минимальное разделение, dп, между точками.[1] Чтобы преобразовать эти две формулировки задачи, квадратная сторона единичных кругов будет .
Решения (не обязательно оптимальные) были вычислены для каждого N≤10,000.[2] Решения до N= 20 показаны ниже:[2]
| Количество кругов (n) | Размер квадрата (длина стороны (L)) | dп[1] | Числовая плотность (n / L ^ 2) | Фигура |
|---|---|---|---|---|
| 1 | 2 | ∞ | 0.25 | |
| 2 | ≈ 3.414... | ≈ 1.414... | 0.172... |  |
| 3 | ≈ 3.931... | ≈ 1.035... | 0.194... |  |
| 4 | 4 | 1 | 0.25 |  |
| 5 | ≈ 4.828... | ≈ 0.707... | 0.215... | 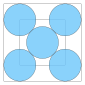 |
| 6 | ≈ 5.328... | ≈ 0.601... | 0.211... |  |
| 7 | ≈ 5.732... | ≈ 0.536... | 0.213... |  |
| 8 | ≈ 5.863... | ≈ 0.518... | 0.233... |  |
| 9 | 6 | 0.5 | 0.25 |  |
| 10 | 6.747... | 0.421... OEIS: A281065 | 0.220... |  |
| 11 | ≈ 7.022... | 0.398... | 0.223... |  |
| 12 | ≈ 7.144... | ≈ 0.389... | 0.235... |  |
| 13 | 7.463... | 0.366... | 0.233... |  |
| 14 | ≈ 7.732... | ≈ 0.349... | 0.226... |  |
| 15 | ≈ 7.863... | ≈ 0.341... | 0.243... |  |
| 16 | 8 | 0.333... | 0.25 |  |
| 17 | 8.532... | 0.306... | 0.234... |  |
| 18 | ≈ 8.656... | ≈ 0.300... | 0.240... |  |
| 19 | 8.907... | 0.290... | 0.240... |  |
| 20 | ≈ 8.978... | ≈ 0.287... | 0.248... |  |
Явная квадратная упаковка оптимальна для 1, 4, 9, 16, 25 и 36 кругов (шесть наименьших квадратные числа ), но перестает быть оптимальным для больших квадратов начиная с 49.[2]
Рекомендации
- ^ а б Croft, Hallard T .; Falconer, Kenneth J .; Гай, Ричард К. (1991). Нерешенные задачи геометрии. Нью-Йорк: Springer-Verlag. стр.108–110. ISBN 0-387-97506-3.
- ^ а б c Эккард Шпехт (20 мая 2010 г.). «Самые известные упаковки равных кругов в квадрате». Получено 25 мая 2010.
| Этот Связанные с элементарной геометрией статья - это заглушка. Вы можете помочь Википедии расширяя это. |
























