Упаковка сфер - Sphere packing

В геометрия, а упаковка сфер это расположение неперекрывающихся сферы внутри вмещающего пространства. Рассматриваемые сферы обычно имеют одинаковый размер, а пространство обычно трехкомпонентное.размерный Евклидово пространство. Однако сфера проблемы с упаковкой могут быть обобщены для рассмотрения неравных сфер, пространств других измерений (где проблема становится упаковка круга в двух измерениях, или гиперсфера упаковка в более высоких размерах) или неевклидов такие пространства, как гиперболическое пространство.
Типичная проблема упаковки сфер - найти такую компоновку, при которой сферы занимают как можно больше пространства. Пропорция пространства, заполненного сферами, называется плотностью расположения. Поскольку локальная плотность упаковки в бесконечном пространстве может варьироваться в зависимости от объема, в котором она измеряется, обычно проблема заключается в максимальном увеличении средний или же асимптотический плотность, измеренная в достаточно большом объеме.
Для равных сфер в трех измерениях самая плотная упаковка занимает примерно 74% объема. Случайная упаковка равных сфер обычно имеет плотность около 64%.
Классификация и терминология
А решетка аранжировка (обычно называемая обычный расположение) - это тот, в котором центры сфер образуют очень симметричный узор, который требует только п однозначно определяемые векторы (в п-размерный Евклидово пространство ). Расположение решеток периодическое. Компоновки, в которых сферы не образуют решетку (часто называемые нерегулярный) все еще может быть периодическим, но также апериодический (собственно говоря непериодический) или же случайный. Решетчатые конструкции легче обрабатывать, чем нестандартные - их высокая степень симметрия облегчает их классификацию и измерение их плотности.
Обычная упаковка

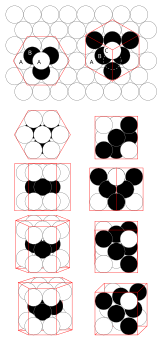

Плотная упаковка
В трехмерном евклидовом пространстве наиболее плотная упаковка равных сфер достигается семейством структур, называемых плотно упакованный конструкции. Один из способов создания такой структуры заключается в следующем. Рассмотрим плоскость с компактным расположением на ней сфер. Назовите это А. Для любых трех соседних сфер четвертую сферу можно поместить сверху в полость между тремя нижними сферами. Если мы сделаем это для половины отверстий во второй плоскости над первой, мы создадим новый компактный слой. Для этого есть два возможных варианта, назовите их B и C. Предположим, что мы выбрали B. Тогда одна половина полостей B лежит над центрами шаров в A, а половина - над полостями A, которые не были используется для B. Таким образом, шары третьего слоя могут быть размещены либо непосредственно над шарами первого слоя, образуя слой типа A, либо над отверстиями первого слоя, которые не были заняты вторым слоем, что дает слой типа C. Комбинирование слоев типов A, B и C дает различные плотноупакованные структуры.
Два простых расположения в пределах семейства плотно упакованных соответствуют правильным решеткам. Один называется кубической плотной упаковкой (или гранецентрированная кубическая, «FCC») - где слои чередуются в последовательности ABCABC ... Другой называется гексагональной плотной упаковкой («HCP»), где слои чередуются в последовательности ABAB ... Но возможно множество последовательностей наложения слоев (ABAC, ABCBA, ABCBAC и т. Д.), Которые по-прежнему создают плотноупакованную структуру. Во всех этих схемах каждая сфера касается 12 соседних сфер,[1] а средняя плотность
Карл Фридрих Гаусс в 1831 году доказал, что эти упаковки имеют самую высокую плотность среди всех возможных решетчатых упаковок.[2]
В 1611 г. Иоганн Кеплер предположили, что это максимально возможная плотность как среди регулярных, так и среди нерегулярных расположений - это стало известно как Гипотеза Кеплера. В 1998 г. Томас Каллистер Хейлз, следуя подходу, предложенному Ласло Фейес Тот в 1953 г. объявил о доказательстве гипотезы Кеплера. Доказательство Хейлза - это доказательство исчерпания включая проверку многих индивидуальных случаев с использованием сложных компьютерных расчетов. Судьи заявили, что они «на 99% уверены» в правильности доказательства Хейлза. 10 августа 2014 г. Хейлз объявил о завершении формального доказательства с использованием автоматическая проверка документов, устраняя любые сомнения.[3]
Другие распространенные решетчатые насадки
Некоторые другие решетчатые упаковки часто встречаются в физических системах. К ним относятся кубическая решетка с плотностью гексагональная решетка с плотностью и тетраэдрическая решетка с плотностью , и наиболее рыхлый при плотности 0,0555.[4]
Застрявшие упаковки с низкой плотностью
Упаковки, в которых все сферы вынуждены соседями оставаться в одном месте, называются жесткими или жесткими. заклинило. Строго заклинивающая упаковка сфер с наименьшей плотностью представляет собой разбавленный («туннелированный») кристалл ГЦК с плотностью всего 0,49365.[5]
Нерегулярная упаковка
Если мы попытаемся построить плотно упакованный набор сфер, у нас будет искушение всегда помещать следующую сферу в полость между тремя упакованными сферами. Если пять сфер собраны таким образом, они будут соответствовать одной из описанных выше схем регулярной упаковки. Однако шестая сфера, размещенная таким образом, сделает структуру несовместимой с обычным расположением. Это приводит к возможности случайная плотная упаковка сфер, устойчивых к сжатию.[6] Вибрация случайной рыхлой упаковки может привести к расположению сферических частиц в регулярные упаковки - процесс, известный как гранулированная кристаллизация. Такие процессы зависят от геометрии контейнера, в котором находятся сферические зерна.[1]
Когда сферы случайным образом добавляются в контейнер, а затем сжимаются, они обычно образуют так называемую «неправильную» или «застрявшую» конфигурацию упаковки, когда их больше нельзя сжимать. Эта неправильная насадка обычно имеет плотность около 64%. Недавние исследования аналитически предсказывают, что он не может превышать предел плотности в 63,4%.[7] Эта ситуация отличается от случая с одним или двумя измерениями, где сжатие набора одномерных или двухмерных сфер (то есть отрезков прямых или окружностей) приведет к регулярной упаковке.
Упаковка гиперсферы
Задача упаковки сфер - это трехмерная версия класса задач упаковки шариков произвольной размерности. В двух измерениях эквивалентная проблема упаковочные круги на плоскости. В одном измерении это упаковка отрезков линий в линейную вселенную.[8]
В размерах больше трех известны наиболее плотные регулярные упаковки гиперсфер до восьми измерений.[9] О нерегулярных гиперсферных упаковках известно очень мало; возможно, что в некоторых измерениях самая плотная упаковка может быть неправильной. Некоторая поддержка этой гипотезы исходит из того факта, что в определенных размерах (например, 10) самая плотная известная нерегулярная упаковка более плотная, чем самая плотная известная регулярная упаковка.[10]
В 2016 г. Марина Вязовская объявил доказательство того, что E8 решетка обеспечивает оптимальную упаковку (независимо от регулярности) в восьмимерном пространстве,[11] и вскоре после этого она и группа сотрудников объявили аналогичное доказательство того, что Решетка пиявки оптимален в 24 измерениях.[12] Этот результат основан на и улучшил предыдущие методы, которые показали, что эти две решетки очень близки к оптимальным.[13]Новые доказательства предполагают использование Преобразование Лапласа тщательно отобранных модульная функция построить радиально симметричный функция ж такой, что ж и это преобразование Фурье f̂ оба равны источник, и оба обращаются в нуль во всех остальных точках оптимальной решетки, причем ж негатив вне центральной сферы упаковки и f̂ положительный. Затем Формула суммирования Пуассона за ж используется для сравнения плотности оптимальной решетки с плотностью любой другой упаковки.[14] До того, как доказательство было формально рефери и опубликовал, математик Питер Сарнак назвал доказательство «потрясающе простым» и написал, что «вы просто начинаете читать статью и знаете, что это правильно».[15]
Другое направление исследований в больших измерениях - попытка найти асимптотический оценки плотности наиболее плотных упаковок. По состоянию на 2017 год известно, что для крупных п, наиболее плотная решетка в размерности п имеет плотность между сп · 2-п (для некоторого постоянного c) и 2-.599п.[16] Предположительные границы лежат посередине.[17]
Неравномерная упаковка сфер

Многие проблемы в химических и физических науках могут быть связаны с задачами упаковки, когда доступны сферы более одного размера. Здесь есть выбор между разделением сфер на области плотно упакованных равных сфер или объединением сфер нескольких размеров в соединение или межстраничный упаковка. Когда сферы многих размеров (или распределение ) доступны, проблема быстро становится трудноразрешимой, но некоторые исследования бинарных твердых сфер (двух размеров) доступны.
Когда вторая сфера намного меньше первой, можно расположить большие сферы плотно упакованными, а затем расположить маленькие сферы внутри октаэдрических и тетраэдрических зазоров. Плотность этой промежуточной упаковки сильно зависит от отношения радиусов, но в пределе крайних соотношений размеров меньшие сферы могут заполнять зазоры с такой же плотностью, как и большие сферы, заполняющие пространство.[19] Даже если большие сферы не расположены плотно упакованными, всегда можно вставить несколько меньших сфер с радиусом до 0,29099 радиуса большей сферы.[20]
Когда меньшая сфера имеет радиус, превышающий 0,41421 радиуса большей сферы, больше невозможно поместиться даже в октаэдрические отверстия плотноупакованной структуры. Таким образом, за пределами этой точки либо структура-хозяин должна расширяться, чтобы вместить межузельные слои (что снижает общую плотность), либо перестраиваться в более сложную структуру кристаллического соединения. Известны структуры, превышающие плотность плотной упаковки для отношений радиусов до 0,659786.[18][21]
Получены также верхние оценки плотности, которая может быть получена в таких бинарных упаковках.[22]
Во многих химических ситуациях, таких как ионные кристаллы, то стехиометрия сдерживается зарядами составляющих ионов. Это дополнительное ограничение на упаковку вместе с необходимостью минимизировать Кулоновская энергия взаимодействующих зарядов приводит к разнообразию оптимальных упаковок.
Гиперболическое пространство
Хотя понятие кругов и сфер можно распространить на гиперболическое пространство, найти наиболее плотную упаковку становится намного труднее. В гиперболическом пространстве нет ограничений на количество сфер, которые могут окружать другую сферу (например, Круги Форда можно рассматривать как набор идентичных гиперболических кругов, в которых каждый круг окружен бесконечный количество других кругов). Понятие средней плотности также становится все труднее точно определить. Самые плотные упаковки в любом гиперболическом пространстве почти всегда нерегулярны.[23]
Несмотря на эту трудность, К. Бёрёчки дает универсальную верхнюю оценку плотности сферических упаковок гиперболических п-пространство, где п ≥ 2.[24] В трех измерениях граница Бёрёчки составляет примерно 85,327613% и реализуется горосфера упаковка четырехгранные соты порядка 6 с Символ Шлефли {3,3,6}.[25] В дополнение к этой конфигурации как минимум три других горосфера Как известно, в трехмерном гиперболическом пространстве существуют упаковки, реализующие верхнюю границу плотности.[26]
Прикосновение к парам, тройкам и четверкам
В график контактов произвольной конечной упаковки единичных шаров - это граф, вершины которого соответствуют элементам упаковки, а две вершины соединены ребром, если соответствующие два элемента упаковки касаются друг друга. Мощность набора ребер графа контактов дает количество соприкасающихся пар, количество 3-циклов в графе контактов дает количество соприкасающихся троек, а количество тетраэдров в графе контактов дает количество соприкасающихся четверок ( в общем случае для контактного графа, связанного с упаковкой сферы в п размеры, что мощность множества п-симплексы в графе контактов дают количество касаний (п + 1) -наборы в упаковке сфер). В случае 3-мерного евклидова пространства нетривиальные оценки сверху количества соприкасающихся пар, троек и четверок[27] были доказаны Кароли Бездек и Сэмюэл Рид из Университета Калгари.
Проблема нахождения расположения п одинаковых сфер, которые максимизируют количество точек контакта между сферами, известна как «проблема липких сфер». Максимум известен п ≤ 11, и известны только предположительные значения для больших п.[28]
Другие пространства
Упаковка сфер по углам гиперкуба (со сферами, определяемыми Расстояние Хэмминга ) соответствует проектированию коды с исправлением ошибок: если сферы имеют радиус т, то их центры являются кодовыми словами a (2т + 1) -код исправления ошибок. Упаковки решеток соответствуют линейным кодам. Есть и другие, более тонкие отношения между упаковкой евклидовой сферы и кодами исправления ошибок. Например, двоичный код Голея тесно связана с 24-мерной решеткой Лича.
Подробнее об этих подключениях см. Книгу Сферические упаковки, решетки и группы к Конвей и Sloane.[29]
Смотрите также
- Плотная упаковка равных сфер
- Упаковка аполлонических сфер
- Постоянная Эрмита
- Проблема с поцелуями
- Связанная сфера-упаковка
- Случайная близкая упаковка
- Набивка цилиндрической сферы
Рекомендации
- ^ а б Кристаллизация гранул в вибрирующих насадках Гранулированное вещество (2019), 21 (2), 26 HAL Archives Ouvertes
- ^ Гаус, К.Ф. (1831 г.). "Besprechung des Buchs von L.A. Seeber": Untersuchungen über die Eigenschaften der positiven ternären quadratischen Formen usw »[Обсуждение книги Л. А. Сибера: Исследования характеристик положительных тернарных квадратичных форм так далее]. Göttingsche Gelehrte Anzeigen.
- ^ «Долгосрочное хранилище для хостинга проектов Google Code». Архив Google Code.
- ^ «Мир Wolfram Math, упаковка сфер».
- ^ Торквато, С.; Стиллинджер, Ф. Х. (2007). «К порогу заклинивания сферических упаковок: туннельные кристаллы». Журнал прикладной физики. 102 (9): 093511–093511–8. arXiv:0707.4263. Bibcode:2007JAP ... 102i3511T. Дои:10.1063/1.2802184. S2CID 5704550.
- ^ Чайкин, Пол (июнь 2007). "Случайные мысли". Физика сегодня. Американский институт физики. 60 (6): 8. Bibcode:2007ФТ .... 60ф ... 8С. Дои:10.1063/1.2754580. ISSN 0031-9228.
- ^ Песня, C .; Wang, P .; Максе, Х.А. (29 мая 2008 г.). «Фазовая диаграмма застрявшей материи». Природа. 453 (7195): 629–632. arXiv:0808.2196. Bibcode:2008Натура.453..629S. Дои:10.1038 / природа06981. PMID 18509438. S2CID 4420652.
- ^ Гриффит, Дж. (1962). «Упаковка ровных 0-сфер». Природа. 196 (4856): 764–765. Bibcode:1962Натура.196..764Г. Дои:10.1038 / 196764a0. S2CID 4262056.
- ^ Вайсштейн, Эрик В. «Гиперсферная упаковка». MathWorld.
- ^ Слоан, Н. Дж. А. (1998). «Проблема упаковки сфер». Documenta Mathematica. 3: 387–396. arXiv:математика / 0207256. Bibcode:2002математика ...... 7256S.
- ^ Вязовская, Марина (1 января 2017 г.). «Проблема упаковки сфер в размерности 8». Анналы математики. 185 (3): 991–1015. arXiv:1603.04246. Дои:10.4007 / анналы.2017.185.3.7. ISSN 0003-486X. S2CID 119286185.
- ^ Кон, Генри; Кумар, Абхинав; Миллер, Стивен; Радченко, Данило; Вязовская, Марина (1 января 2017 г.). «Проблема упаковки сфер в размерности 24». Анналы математики. 185 (3): 1017–1033. arXiv:1603.06518. Дои:10.4007 / анналы.2017.185.3.8. ISSN 0003-486X. S2CID 119281758.
- ^ Кон, Генри; Кумар, Абхинав (2009), "Оптимальность и единственность решетки Пиявки среди решеток", Анналы математики, 170 (3): 1003–1050, arXiv:math.MG/0403263, Дои:10.4007 / анналы.2009.170.1003, ISSN 1939-8980, МИСТЕР 2600869, S2CID 10696627, Zbl 1213.11144 Кон, Генри; Кумар, Абхинав (2004), "Самая плотная решетка в двадцати четырех измерениях", Объявления об электронных исследованиях Американского математического общества, 10 (7): 58–67, arXiv:math.MG/0408174, Дои:10.1090 / S1079-6762-04-00130-1, ISSN 1079-6762, МИСТЕР 2075897, S2CID 15874595
- ^ Миллер, Стивен Д. (4 апреля 2016 г.), Решение проблемы упаковки сфер в 24 измерениях с помощью модульных форм, Институт перспективных исследований. Видео часового выступления одного из соавторов Вязовской с объяснением новых доказательств.
- ^ Кларрайх, Эрика (30 марта 2016 г.), «Сферическая упаковка решена в более высоких измерениях», Журнал Quanta
- ^ Кон, Генри (2017), «Концептуальный прорыв в сфере упаковки» (PDF), Уведомления Американского математического общества, 64 (2): 102–115, arXiv:1611.01685, Дои:10.1090 / noti1474, ISSN 0002-9920, МИСТЕР 3587715, S2CID 16124591
- ^ Torquato, S .; Стиллинджер, Ф. Х. (2006), «Новые гипотетические нижние оценки оптимальной плотности упаковки сфер», Экспериментальная математика, 15 (3): 307–331, arXiv:математика / 0508381, Дои:10.1080/10586458.2006.10128964, МИСТЕР 2264469, S2CID 9921359
- ^ а б O'Toole, P. I .; Хадсон, Т. С. (2011). "Новые высокоплотные упаковки бинарных сфер аналогичного размера". Журнал физической химии C. 115 (39): 19037. Дои:10.1021 / jp206115p.
- ^ Хадсон, Д. Р. (1949). «Плотность и упаковка в совокупности смешанных сфер». Журнал прикладной физики. 20 (2): 154–162. Bibcode:1949JAP .... 20..154H. Дои:10.1063/1.1698327.
- ^ Цзун, К. (2002). «От глубоких ям до свободных плоскостей». Бюллетень Американского математического общества. 39 (4): 533–555. Дои:10.1090 / S0273-0979-02-00950-3.
- ^ Marshall, G.W .; Хадсон, Т. С. (2010). «Плотные бинарные упаковки сфер». Вклад в алгебру и геометрию. 51 (2): 337–344.
- ^ де Лаат, Давид; де Оливейра Филью, Фернандо Мариу; Валлентин, Франк (12 июня 2012 г.). «Верхние границы для упаковки сфер нескольких радиусов». Форум математики, Сигма. 2. arXiv:1206.2608. Дои:10.1017 / fms.2014.24. S2CID 11082628.
- ^ Bowen, L .; Радин, К. (2002). «Плотнейшая упаковка равных сфер в гиперболическом пространстве». Дискретная и вычислительная геометрия. 29: 23–39. Дои:10.1007 / s00454-002-2791-7.
- ^ Böröczky, К. (1978). «Упаковка сфер в пространства постоянной кривизны». Acta Mathematica Academiae Scientiarum Hungaricae. 32 (3–4): 243–261. Дои:10.1007 / BF01902361. S2CID 122561092.
- ^ Böröczky, K .; Флориан, А. (1964). "Über die dichteste Kugelpackung im hyperbolischen Raum". Acta Mathematica Academiae Scientiarum Hungaricae. 15 (1–2): 237–245. Дои:10.1007 / BF01897041. S2CID 122081239.
- ^ Козьма, Р. Т .; Сирмаи, Дж. (2012). «Оптимально плотные упаковки для полностью асимптотических разбиений Кокстера гороболами разных типов». Monatshefte für Mathematik. 168: 27–47. arXiv:1007.0722. Дои:10.1007 / s00605-012-0393-х. S2CID 119713174.
- ^ Бездек, Кароли; Рид, Самуэль (2013). "Обратимся к контактным графам сферических упаковок". Журнал геометрии. 104 (1): 57–83. arXiv:1210.5756. Дои:10.1007 / s00022-013-0156-4. S2CID 14428585.
- ^ «Наука липких сфер». Американский ученый. 6 февраля 2017 г.. Получено 14 июля 2020.
- ^ Конвей, Джон Х.; Слоан, Нил Дж. А. (1998). Сферические упаковки, решетки и группы (3-е изд.). Springer Science & Business Media. ISBN 0-387-98585-9.
Библиография
- Aste, T .; Уир, Д. (2000). В поисках идеальной упаковки. Лондон: Издательский институт физики. ISBN 0-7503-0648-3.
- Конвей, Дж. Х.; Слоан, Н. Дж. Х. (1998). Сферические упаковки, решетки и группы (3-е изд.). ISBN 0-387-98585-9.
- Слоан, Н. Дж. А. (1984). «Упаковка сфер». Scientific American. 250: 116–125. Bibcode:1984SciAm.250e.116G. Дои:10.1038 / scientificamerican0584-116.
внешняя ссылка
- Дана Маккензи (май 2002 г.) "Прекрасный беспорядок" (Новый ученый)
- Нетехнический обзор упаковки в гиперболическом пространстве.
- Вайсштейн, Эрик В. «Круглая упаковка». MathWorld.
- "Kugelpackungen (сферическая упаковка)" (Т.Е. Дорожинский)
- "Апплет упаковки 3D-сферы" Java-апплет Sphere Packing
- «Плотнейшая упаковка сфер в сферу» Java-апплет
- «База данных сферических упаковок» (Эрик Агрелл)




