Сфера - Sphere

Двумерный перспективная проекция сферы

А сфера (из Греческий σφαῖρα—Sphaira, "глобус, мяч"^[1]) это геометрический объект в трехмерное пространство это поверхность мяч (то есть аналогично круглым объектам в двух измерениях, где "круг "ограничивает "диск" ).

Как круг в двумерном пространстве, сфера математически определяется как набор точек все на одинаковом расстоянии р из заданной точки в трехмерном пространстве.^[2] Это расстояние р это радиус мяча, составленного из всех точек с расстоянием меньше (или, для закрытого мяча, меньше чем или равно) р из данной точки, которая является центр математического мяча. Их также называют радиусом и центром сферы соответственно. Самый длинный отрезок прямой через шар, соединяющий две точки сферы, проходит через центр, и его длина, таким образом, в два раза больше радиуса; это диаметр как сферы, так и ее шара.

Вне математики термины «сфера» и «шар» иногда используются как синонимы, в математика указанное выше различие проводится между сфера, который является двумерным закрытая поверхность встроенный в трехмерном Евклидово пространство, а мяч, который представляет собой трехмерную фигуру, которая включает в себя сферу и все внутри сфера (a закрытый мяч), а чаще просто точки внутри, но не на сфера (an открытый мяч). Различие между мяч и сфера не всегда поддерживается, и особенно старые математические ссылки говорят о сфере как о твердом теле. Это аналогично ситуации в самолет, где также можно путать термины «круг» и «диск».

Уравнения в трехмерном пространстве

Два ортогональных радиуса сферы

В аналитическая геометрия, сфера с центром (Икс₀, у₀, z₀) и радиус р это локус всех точек (Икс, у, z) такой, что

${displaystyle (x-x_ {0}) ^ {2} + (y-y_ {0}) ^ {2} + (z-z_ {0}) ^ {2} = r ^ {2}.}$

Позволять а, б, в, г, д быть реальными числами с а ≠ 0 и положи

${displaystyle x_ {0} = {frac {-b} {a}}, quad y_ {0} = {frac {-c} {a}}, quad z_ {0} = {frac {-d} {a}) }, quad ho = {frac {b ^ {2} + c ^ {2} + d ^ {2} -ae} {a ^ {2}}}.}.$

Тогда уравнение

${displaystyle f (x, y, z) = a (x ^ {2} + y ^ {2} + z ^ {2}) + 2 (bx + cy + dz) + e = 0}$

не имеет реальных точек в качестве решений, если ${displaystyle ho <0}$ и называется уравнением воображаемая сфера. Если ${displaystyle ho = 0}$, единственное решение ${displaystyle f (x, y, z) = 0}$ это суть ${displaystyle P_ {0} = (x_ {0}, y_ {0}, z_ {0})}$ и уравнение называется уравнением точечная сфера. Наконец, в случае ${displaystyle ho> 0}$, ${displaystyle f (x, y, z) = 0}$ уравнение сферы с центром в ${displaystyle P_ {0}}$ и радиус которого ${displaystyle {sqrt {ho}}}$.^[2]

Если а в приведенном выше уравнении равно нулю, тогда ж(Икс, у, z) = 0 - уравнение плоскости. Таким образом, плоскость можно представить себе как сферу бесконечного радиуса с центром в точка в бесконечности.^[3]

Точки на сфере радиуса ${displaystyle r> 0}$ и центр ${displaystyle (x_ {0}, y_ {0}, z_ {0})}$ можно параметризовать через

${displaystyle {egin {выравнивается} x & = x_ {0} + rsin heta; cos varphi y & = y_ {0} + rsin heta; sin varphi qquad (0leq heta leq pi,; 0leq varphi <2pi) z & = z_ { 0} + rcos heta, конец {выровнено}}}$^[4]

Параметр ${displaystyle heta}$ можно связать с углом, отсчитываемым положительно от направления положительного z-ось через центр к радиус-вектору, а параметр ${displaystyle varphi}$ можно связать с углом, отсчитываемым положительно от направления положительного Икс-ось через центр к проекции радиус-вектора на ху-самолет.

Сфера любого радиуса с центром в нуле является интегральной поверхностью следующих дифференциальная форма:

${displaystyle x, dx + y, dy + z, dz = 0.}$

Это уравнение отражает векторы положения и скорости точки, (Икс, у, z) и (dx, dy, дз), путешествующие по сфере всегда ортогональный друг другу.

Сфера также может быть построена как поверхность, образованная вращением круг о любом из его диаметры. Поскольку круг - это особый вид эллипс, сфера - это особый тип эллипсоид вращения. Заменив круг на эллипс, повернутый вокруг большая ось форма становится вытянутой сфероид; вращенный вокруг малой оси, сплюснутый сфероид.^[5]

Закрытый том

Сфера и описанный цилиндр

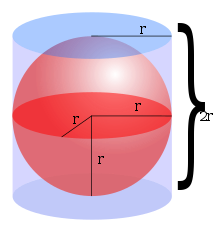
В трех измерениях объем внутри сферы (т. е. объем мяч, но классически называемый объемом сферы)

${displaystyle V = {frac {4} {3}} pi r ^ {3} = {frac {pi} {6}} d ^ {3} примерно 0,5236cdot d ^ {3}}$

куда р это радиус и d диаметр сферы. Архимед впервые вывел эту формулу, показав, что объем внутри сферы вдвое больше объема между сферой и ограниченный цилиндр этой сферы (имеющей высоту и диаметр, равные диаметру сферы).^[6] Это можно доказать, вписав конус в перевернутую полусферу, отметив, что площадь поперечного сечения конуса плюс площадь поперечного сечения сферы такая же, как и площадь поперечного сечения описывающего цилиндра. , и применяя Принцип Кавальери.^[7] Эта формула также может быть получена с использованием интегральное исчисление, т.е. интеграция с дисками суммировать объемы бесконечное число из круговой диски бесконечно малой толщины, расположенные рядом и центрированные вдоль Икс-ось от Икс = −р к Икс = р, считая сферу радиуса р с центром в начале координат.

В любом случае Икс, дополнительный объем (δV) равно произведению поперечного сечения площадь диска в Икс и его толщина (δx):

${displaystyle delta Vapprox pi y ^ {2} cdot delta x.}$

Общий объем - это сумма всех дополнительных объемов:

${displaystyle Vapprox sum pi y ^ {2} cdot delta x.}$

В пределе как δx приближается к нулю,^[8] это уравнение становится:

${displaystyle V = int _ {- r} ^ {r} pi y ^ {2} dx.}$

В любом случае Икс, прямоугольный треугольник соединяет Икс, у и р к происхождению; следовательно, применяя теорема Пифагора дает:

${displaystyle y ^ {2} = r ^ {2} -x ^ {2}.}$

Использование этой замены дает

${displaystyle V = int _ {- r} ^ {r} pi left (r ^ {2} -x ^ {2} ight) dx,}$

которые можно оценить, чтобы дать результат

${displaystyle V = pi left [r ^ {2} x- {frac {x ^ {3}} {3}} ight] _ {- r} ^ {r} = pi left (r ^ {3} - {frac {r ^ {3}} {3}} ight) -pi left (-r ^ {3} + {frac {r ^ {3}} {3}} ight) = {frac {4} {3}} pi г ^ {3}.}$

Альтернативная формула находится с использованием сферические координаты, с элемент объема

${displaystyle dV = r ^ {2} sin heta, dr, d heta, dvarphi}$

так

${displaystyle V = int _ {0} ^ {2pi} int _ {0} ^ {pi} int _ {0} ^ {r} r '^ {2} sin heta, dr', d heta, dvarphi = 2pi int _ {0} ^ {pi} int _ {0} ^ {r} r '^ {2} sin heta, dr', d heta = 4pi int _ {0} ^ {r} r '^ {2}, dr '= {frac {4} {3}} pi r ^ {3}.}$

Для большинства практических целей объем внутри сферы вписанный в кубе может быть приблизительно равно 52,4% от объема куба, поскольку V = π/6 d³, куда d диаметр сферы, а также длина стороны куба и π/6 ≈ 0,5236. Например, сфера диаметром 1 м имеет 52,4% объема куба с длиной ребра 1 м, или около 0,524 м³.

Площадь поверхности

В площадь поверхности сферы радиуса р является:

${displaystyle A = 4pi r ^ {2}.}$

Архимед впервые вывел эту формулу^[9] от того, что проекция на боковую поверхность ограниченный цилиндр сохраняет площадь.^[10] Другой подход к получению формулы исходит из того факта, что она равна производная формулы для объема относительно р потому что общий объем внутри сферы радиуса р можно представить себе как сумму площади поверхности бесконечного числа сферических оболочек бесконечно малой толщины, концентрически уложенных друг в друга от радиуса 0 до радиуса р. При бесконечно малой толщине несоответствие между площадью внутренней и внешней поверхности любой заданной оболочки бесконечно мало, и элементарный объем на радиусе р просто произведение площади поверхности на радиус р и бесконечно малую толщину.

В любом заданном радиусе р,^{[примечание 1]} дополнительный объем (δV) равняется произведению площади поверхности на радиус р (А(р)) и толщину оболочки (δr):

${displaystyle delta Vapprox A (r) cdot delta r.}$

Общий объем - это сумма всех объемов оболочки:

${displaystyle Vapprox sum A (r) cdot delta r.}$

В пределе как δr приближается к нулю^[8] это уравнение становится:

${displaystyle V = int _ {0} ^ {r} A (r), dr.}$

Заменять V:

${displaystyle {frac {4} {3}} pi r ^ {3} = int _ {0} ^ {r} A (r), dr.}$

Дифференцируя обе части этого уравнения по р дает А как функция р:

${displaystyle 4pi r ^ {2} = A (r).}$

Обычно это сокращается как:

${displaystyle A = 4pi r ^ {2},}$

куда р теперь считается фиксированным радиусом сферы.

В качестве альтернативы элемент площади на сфере дано в сферические координаты к dA = р² грех θ dθ dφ. В Декартовы координаты, элемент площади^{[нужна цитата ]}

${displaystyle dS = {frac {r} {sqrt {r ^ {2} - {displaystyle sum _ {ieq k} x_ {i} ^ {2}}}}} prod _ {ieq k} dx_ {i} ,; forall k.}$

Таким образом, общая площадь может быть получена интеграция:

${displaystyle A = int _ {0} ^ {2pi} int _ {0} ^ {pi} r ^ {2} sin heta, d heta, dvarphi = 4pi r ^ {2}.}$

Сфера имеет наименьшую площадь поверхности из всех поверхностей, которые охватывают данный объем, и включает в себя наибольший объем среди всех закрытых поверхностей с данной площадью поверхности.^[11] Таким образом, сфера появляется в природе: например, пузырьки и маленькие капли воды имеют примерно сферическую форму, потому что поверхностное натяжение локально минимизирует площадь поверхности.

Площадь поверхности относительно массы шара называется удельная поверхность и может быть выражено из приведенных выше уравнений как

${displaystyle mathrm {SSA} = {frac {A} {Vho}} = {frac {3} {rho}},}$

куда ρ это плотность (отношение массы к объему).

Кривые на сфере

Плоское сечение сферы: 1 круг

Коаксиальное пересечение сферы и цилиндра: 2 круга

Круги

• Пересечение сферы и плоскости - это круг, точка или пустота.

В случае круга его можно описать параметрическое уравнение ${displaystyle; {vec {x}} = ({vec {e}} _ {0} + {vec {e}} _ {1} cos t + {vec {e}} _ {2} sin t) ^ {T };}$: см. плоский разрез эллипсоид.

Но более сложные поверхности могут также пересекать сферу по кругу:

• Непустое пересечение сферы с поверхность вращения, ось которого проходит через центр сферы (являются коаксиальный) состоит из кружков и / или точек.

На схеме показан случай, когда точка пересечения цилиндра и сферы состоит из двух окружностей. Если бы радиус цилиндра был равен радиусу сферы, пересечение было бы одним кругом, где обе поверхности касаются друг друга.

В случае сфероида с тем же центром и большой осью, что и сфера, пересечение будет состоять из двух точек (вершин), где поверхности касаются друг друга.

Клелия кривые

сферическая спираль с ${displaystyle c = 8}$

Если сфера описывается параметрическим представлением

${displaystyle {vec {x}} = (rcos heta cos varphi, rcos heta sin varphi, rsin heta) ^ {T}}$

один получает Клелия кривые, если углы связаны уравнением

• ${displaystyle varphi = c; heta;, c> 0 ;.}$

Особые случаи: Кривая Вивиани (${displaystyle c = 1}$) и сферические спирали (${displaystyle c> 2}$).

Локсодромия

Локсодромия

В навигация, а линия румба или же локсодромия дуга пересекает все меридианы из долгота под таким же углом. Линия румба - это не сферическая спираль. Между углами нет простой связи ${displaystyle varphi}$ и ${displaystyle heta}$.

Пересечение сферы с более общей поверхностью

Общее пересечение сфера-цилиндр

Если сфера пересекается другой поверхностью, могут быть более сложные сферические кривые.

Пример: сфера - цилиндр

Пересечение сферы с уравнением ${displaystyle; x ^ {2} + y ^ {2} + z ^ {2} = r ^ {2};}$ и цилиндр с уравнением ${displaystyle; (y-y_ {0}) ^ {2} + z ^ {2} = a ^ {2} ,; y_ {0} eq 0;}$ это не просто один или два круга. Это решение нелинейной системы уравнений

${displaystyle x ^ {2} + y ^ {2} + z ^ {2} -r ^ {2} = 0}$

${displaystyle (y-y_ {0}) ^ {2} + z ^ {2} -a ^ {2} = 0.}$

(видеть неявная кривая и диаграмма)

Геометрические свойства

Сфера однозначно определяется четырьмя точками, которые не являются копланарный. В более общем плане сфера однозначно определяется четырьмя условиями, такими как прохождение через точку, касание к плоскости и т. Д.^[12] Это свойство аналогично тому, что три неколлинеарный точки определяют уникальный круг на плоскости.

Следовательно, сфера однозначно определяется окружностью (то есть проходит через нее) и точкой, не лежащей в плоскости этой окружности.

Изучив общие решения уравнений двух сфер, можно видеть, что две сферы пересекаются по кругу, и плоскость, содержащая этот круг, называется радикальный самолет пересекающихся сфер.^[13] Хотя радикальная плоскость является реальной плоскостью, круг может быть воображаемым (у сфер нет общей реальной точки) или состоять из одной точки (сферы касаются в этой точке).^[14]

Угол между двумя сферами в реальной точке пересечения равен двугранный угол определяется касательными плоскостями к сферам в этой точке. Две сферы пересекаются под одним и тем же углом во всех точках их круга пересечения.^[15] Они пересекаются под прямым углом (являются ортогональный ) тогда и только тогда, когда квадрат расстояния между их центрами равен сумме квадратов их радиусов.^[3]

Карандаш из сфер

Если ж(Икс, у, z) = 0 и грамм(Икс, у, z) = 0 являются уравнениями двух различных сфер, то

${displaystyle sf (x, y, z) + tg (x, y, z) = 0}$

также является уравнением шара для произвольных значений параметров s и т. Множество всех сфер, удовлетворяющих этому уравнению, называется карандаш сфер определяется двумя исходными сферами. В этом определении сфера может быть плоскостью (бесконечный радиус, центр в бесконечности), и если обе исходные сферы являются плоскостями, тогда все сферы пучка являются плоскостями, в противном случае в плоскости есть только одна плоскость (радикальная плоскость). карандаш.^[3]

Терминология

Плоские секции

А большой круг на сфере имеет тот же центр и радиус, что и сфера, следовательно, делит ее на две равные части. В плоские сечения сферы называются сферические разрезы -которые представляют собой либо большие круги для плоскостей, проходящих через центр сферы, либо маленькие круги для всех остальных.^[16]

Любая плоскость, которая включает центр сферы, делит ее на две равные части. полушария. Любые две пересекающиеся плоскости, которые включают центр сферы, делят сферу на четыре части. люны или двуугольников, вершины которых совпадают с противоположные точки лежащий на линии пересечения плоскостей.

Отрасли геометрии

Неевклидово расстояние

Любая пара точек на сфере, лежащих на прямой, проходящей через центр сферы (т.е. диаметр), называется противоположные точки - на сфере расстояние между ними ровно половину длины окружности.^{[заметка 2]} Любая другая (т. Е. Не антиподальная) пара различных точек на сфере

• лежать на уникальном большом круге,
• сегментируйте его на один второстепенный (т.е. более короткий) и один большой (т.е. более длинный) дуга, и
• длина вспомогательной дуги должна быть кратчайшее расстояние между ними на сфере.^{[заметка 3]}

Сферическая геометрия^{[примечание 4]} имеет много аналогичных свойств Евклидово однажды оснащенный этим "расстояние по дуге ".

Дифференциальная геометрия

И многое другое абстрактное обобщение геометрии также использует ту же концепцию расстояния в Риманов круг.

Полушарие предполагаемый быть оптимальным (с наименьшей площадью) изометрическим заполнением Риманов круг.

Проективная геометрия

Антиподальное частное сферы - это поверхность, называемая реальная проективная плоскость, который также можно рассматривать как Северное полушарие с выделенными точками, противоположными экватору.

География

Термины, заимствованные непосредственно из географии земной шар, несмотря на сфероидальный форма, имеющая большее или меньшее отклонение от идеальной сферы (см. геоид ), широко понятны. В геометрии, не связанной с астрономическими телами, геоцентрическая терминология должна использоваться только для иллюстрации и отметил как таковой, если нет возможности недопонимания.

Поляки, долгота и широта

Если определенная точка на сфере (произвольно) обозначена как ее Северный полюс, его антиподальная точка называется Южный полюс. Большой круг, равноотстоящий друг от друга, будет экватор. Большие круги, проходящие через полюса, называются линиями долгота (или же меридианы ). Линия не на сфере но через его центр, соединяющий два полюса май называться ось вращения. Окружности на сфере, параллельные экватору (т. Е. Не большие круги), являются линиями широта.

Обобщения

Размерность

Сферы можно обобщить на пространства любого числа размеры. Для любого натуральное число п, "п-сфера », часто пишется как S^п, - множество точек в (п + 1) -мерное евклидово пространство, находящиеся на фиксированном расстоянии р из центральной точки этого пространства, где р по-прежнему является положительным действительным числом. Особенно:

• S⁰: 0-сфера - это пара концов интервала [−р, р] реальной линии
• S¹: 1-сфера - это круг радиуса р
• S²: 2-сфера - это обычная сфера
• S³: а 3-сфера является сферой в 4-мерном евклидовом пространстве.

Сферы для п > 2 иногда называют гиперсферы.

В п-сфера единичного радиуса с центром в начале координат обозначается S^п и часто упоминается как " п-сфера. Обратите внимание, что обычная сфера - это 2-сфера, потому что это 2-мерная поверхность (которая вложена в 3-мерное пространство).

Площадь агрегата (п-1) -сфера есть

${displaystyle {frac {2pi ^ {frac {n} {2}}} {Гамма слева ({frac {n} {2}} ight)}}}$

куда Γ (z) Эйлера гамма-функция.

Другое выражение для площади поверхности:

${displaystyle {egin {cases} displaystyle {frac {(2pi) ^ {n / 2}, r ^ {n-1}} {2cdot 4cdots (n-2)}}, & {ext {if}} n {ext {четно}}; displaystyle {frac {2 (2pi) ^ {(n-1) / 2}, r ^ {n-1}} {1cdot 3cdots (n-2)}}, & {ext { if}} n {ext {нечетное}}. end {case}}}$

а объем - это площадь поверхности, умноженная на р/п или же

${displaystyle {egin {case} displaystyle {frac {(2pi) ^ {n / 2}, r ^ {n}} {2cdot 4cdots n}}, & {ext {if}} n {ext {даже}}; displaystyle {frac {2 (2pi) ^ {(n-1) / 2}, r ^ {n}} {1cdot 3cdots n}}, & {ext {if}} n {ext {is odd}}. конец {case}}}$

Общие рекурсивные формулы существуют также для объем п-мяч.

Метрические пространства

В общем, в метрическое пространство (E,d), сфера центра Икс и радиус р > 0 это набор точек у такой, что d(Икс,у) = р.

Если центр - это выделенная точка, которая считается источником E, как в нормированный пробел, в определении и обозначениях он не упоминается. То же самое относится и к радиусу, если он принимается равным единице, как в случае с единичная сфера.

В отличие от мяч, даже большая сфера может быть пустым множеством. Например, в Z^п с Евклидова метрика, сфера радиуса р непусто, только если р² можно записать как сумму п квадраты целые числа.

Топология

В топология, п-сфера определяется как пространство гомеоморфный к границе (п + 1)-мяч; таким образом, это гомеоморфный к евклидову п-сфера, но, возможно, не хватает ее метрика.

• 0-сфера - это пара точек с дискретная топология.
• 1-сфера - это круг (вплоть до гомеоморфизм ); так, например, (изображение) любой морской узел является 1-сферой.
• 2-сфера - это обычная сфера (вплоть до гомеоморфизм ); так, например, любой сфероид является 2-сферой.

В п-сфера обозначается S^п. Это пример компактный топологическое многообразие без граница. Сфера не обязательно гладкий; если гладко, то не обязательно диффеоморфный к евклидовой сфере ( экзотическая сфера ).

В Теорема Гейне – Бореля следует, что евклидова п-сфера компактная. Сфера - это прообраз одноточечного множества при непрерывной функции ||Икс||. Следовательно, сфера замкнута. S^п также ограничен; поэтому он компактный.

Примечательно, что обычный шар можно вывернуть наизнанку. трехмерное пространство с возможными самопересечениями, но без образования складок, в процессе, называемом выворот сферы.

Сферическая геометрия

Большой круг на сфере

Основные элементы Евклидова плоская геометрия находятся точки и линии. На сфере точки определяются в обычном смысле. Аналогом «линии» является геодезический, который является большой круг; Определяющей характеристикой большого круга является то, что плоскость, содержащая все его точки, также проходит через центр сферы. Измерение длина дуги показывает, что кратчайший путь между двумя точками, лежащими на сфере, - это более короткий отрезок большой круг это включает в себя точки.

Многие теоремы из классическая геометрия верно и для сферической геометрии, но не для всех, потому что сфера не удовлетворяет некоторым требованиям классической геометрии. постулаты, в том числе параллельный постулат. В сферическая тригонометрия, углы определены между большими кругами. Сферическая тригонометрия отличается от обычной тригонометрия во многих отношениях. Например, сумма внутренних углов сферический треугольник всегда превышает 180 градусов. Также любые два похожий сферические треугольники конгруэнтны.

Одиннадцать свойств сферы

Вектор нормали к сфере, нормальной плоскости и ее нормальному сечению. Кривизна кривой пересечения - это кривизна секции. Для сферы каждое нормальное сечение через данную точку будет кругом того же радиуса: радиуса сферы. Это означает, что каждая точка на сфере будет точкой пуповины.

В их книге Геометрия и воображение^[17] Дэвид Гильберт и Стефан Кон-Фоссен опишите одиннадцать свойств сферы и обсудите, определяют ли эти свойства однозначно сферу. Для самолет, который можно представить как сферу бесконечного радиуса. Эти свойства:

1. Все точки на сфере находятся на одинаковом расстоянии от фиксированной точки. Также постоянным является отношение расстояния его точек от двух фиксированных точек.

   Первая часть представляет собой обычное определение сферы и однозначно определяет ее. Вторая часть легко выводится и следует аналогичному результат из Аполлоний Пергский для круг. Эта вторая часть также верна для самолет.

2. Контуры и плоские сечения сферы представляют собой окружности.

   Это свойство однозначно определяет сферу.

3. Сфера имеет постоянную ширину и постоянный обхват.

   Ширина поверхности - это расстояние между парами параллельных касательных плоскостей. Многие другие замкнутые выпуклые поверхности имеют постоянную ширину, например Тело Мейснера. Обхват поверхности - это длина окружности границы его ортогональной проекции на плоскость. Каждое из этих свойств подразумевает другое.

4. Все точки сферы пуповина.

   В любой точке поверхности нормальное направление находится под прямым углом к ​​поверхности, потому что сфера - это линии, исходящие из центра сферы. Пересечение плоскости, содержащей нормаль, с поверхностью образует кривую, которая называется нормальный раздел, а кривизна этой кривой равна нормальная кривизна. Для большинства точек на большинстве поверхностей разные секции будут иметь разную кривизну; их максимальное и минимальное значения называются основные кривизны. На любой замкнутой поверхности будет не менее четырех точек, называемых пупочные точки. В шлангокабеле все кривизны в разрезе равны; в частности основные кривизны равны. Пупочные точки можно рассматривать как точки, где поверхность близко аппроксимируется сферой.

   Для сферы кривизны всех нормальных сечений равны, поэтому каждая точка является омбиликой. Сфера и плоскость - единственные поверхности с этим свойством.

5. У сферы нет поверхности центров.

   Для данного нормального сечения существует окружность кривизны, равная кривизне сечения, касательная к поверхности, а центральные линии которой лежат на нормальной линии. Например, два центра, соответствующие максимальной и минимальной кривизне сечения, называются точки фокуса, а совокупность всех таких центров образует фокальная поверхность.

   Для большинства поверхностей фокальная поверхность образует два листа, каждый из которых является поверхностью и соединяется в точках шлангокабеля. Некоторые случаи особенные:

   * За поверхности каналов один лист образует кривую, а другой лист - поверхность

   * За шишки, цилиндры, тори и циклиды оба листа образуют кривые.

   * Для сферы центр каждого соприкасающегося круга находится в центре сферы, а фокальная поверхность образует единую точку. Это свойство уникально для сферы.

6. Все геодезические сферы - замкнутые кривые.

   Геодезические - это кривые на поверхности, которые дают кратчайшее расстояние между двумя точками. Они являются обобщением концепции прямой линии на плоскости. Для сферы геодезические - большие круги. Многие другие поверхности обладают этим свойством.

7. Из всех твердых тел, имеющих данный объем, сфера имеет наименьшую площадь поверхности; из всех твердых тел, имеющих заданную площадь поверхности, сфера имеет наибольший объем.

   Это следует из изопериметрическое неравенство. Эти свойства однозначно определяют сферу, и их можно увидеть в мыльные пузыри: мыльный пузырь будет заключать фиксированный объем, а поверхностное натяжение минимизирует площадь его поверхности для этого объема. Таким образом, свободно плавающий мыльный пузырь приближается к сфере (хотя такие внешние силы, как гравитация, немного искажают форму пузыря). Это также можно увидеть на планетах и ​​звездах, где гравитация минимизирует площадь поверхности больших небесных тел.

8. Сфера имеет наименьшую общую среднюю кривизну среди всех выпуклых тел с данной площадью поверхности.

   В средняя кривизна - это среднее значение двух главных кривизны, которое является постоянным, поскольку две основные кривизны постоянны во всех точках сферы.

9. Сфера имеет постоянную среднюю кривизну.

   Сфера - единственная встроенный поверхность без границ или особенностей с постоянной положительной средней кривизной. Другие такие погружаемые поверхности, как минимальные поверхности имеют постоянную среднюю кривизну.

10. Сфера имеет постоянную положительную гауссову кривизну.

    Гауссова кривизна является произведением двух главных кривизны. Это внутреннее свойство, которое может быть определено путем измерения длины и углов и не зависит от того, как выглядит поверхность. встроенный в космосе. Следовательно, изгиб поверхности не изменит гауссовой кривизны, а другие поверхности с постоянной положительной гауссовой кривизной могут быть получены путем вырезания небольшой щели в сфере и ее изгиба. Все эти другие поверхности будут иметь границы, и сфера - единственная поверхность, у которой отсутствует граница с постоянной положительной гауссовой кривизной. В псевдосфера является примером поверхности с постоянной отрицательной гауссовой кривизной.

11. Сфера превращается в себя с помощью трехпараметрического семейства жестких движений.

    При вращении вокруг любой оси единичная сфера в начале координат отобразит сферу на себя. Любой поворот вокруг линии, проходящей через начало координат, может быть выражен как комбинация поворотов вокруг трехкоординатной оси (см. Углы Эйлера ). Следовательно, существует трехпараметрическое семейство вращений, при котором каждое вращение преобразует сферу в себя; эта семья группа вращения SO (3). Плоскость - единственная другая поверхность с трехпараметрическим семейством преобразований (переносов по Икс- и у-оси и вращения вокруг начала координат). Круглые цилиндры - единственные поверхности с двухпараметрическими семействами жестких движений и поверхности вращения и геликоиды являются единственными поверхностями с однопараметрическим семейством.

Галерея

• 

  Изображение одной из самых точных сфер, созданных руками человека, поскольку оно преломляет образ Эйнштейн на заднем фоне. Эта сфера была плавленый кварц гироскоп для Гравитационный зонд B эксперимента, и отличается по форме от идеальной сферы не более чем на 40 атомов (менее 10 нм) толщины. 1 июля 2008 г. было объявлено, что Австралийский ученые создали еще более почти идеальные сферы с точностью до 0,3 нм, в рамках международной охоты за новым мировым стандартом килограмм.^[18]

• 

  Колода игральных карт с изображением инженерных инструментов, Англия, 1702 год. Король пик: Сферы

Регионы

• Сферическая крышка
• Сферический многоугольник
• Сферический сектор
• Сферический сегмент
• Сферический клин
• Сферическая зона

Смотрите также

Примечания и ссылки

Примечания

Рекомендации

дальнейшее чтение

• Альберт, Авраам Адриан (2016) [1949], Твердая аналитическая геометрия, Дувр, ISBN  978-0-486-81026-3.
• Данэм, Уильям (1997). Математическая вселенная: путешествие по алфавиту через великие доказательства, проблемы и личности. Wiley. Нью-Йорк. стр.28, 226. Bibcode:1994muaa.book ..... D. ISBN  978-0-471-17661-9.
• Крейсциг, Эрвин (1972), Высшая инженерная математика (3-е изд.), Нью-Йорк: Wiley, ISBN  978-0-471-50728-4.
• Штейнхаус, Х. (1969), Математические снимки (Третье американское изд.), Oxford University Press.
• Вудс, Фредерик С. (1961) [1922], Высшая геометрия / Введение в передовые методы аналитической геометрии, Дувр.

внешняя ссылка

• Mathematica / Равномерное сферическое распределение
• Площадь поверхности доказательства сферы