Килограмм - Kilogram

"kg" перенаправляется сюда. Для использования в других целях см. KG (значения).

килограмм
Поидс фонте 1 кг 01.jpg
Общая информация
Система единицБазовая единица СИ
Единицамасса
Символкг
Конверсии
1 кг в ...... равно ...
   Avoirdupois   ≈ 2.204622 фунты[Примечание 1] 
   Британский гравитационный   ≈ 0.0685 слизни  

В килограмм (также килограмм) это базовый блок из масса в Международная система единиц (SI) текущая метрическая система, имеющий символ единицы кг. Это широко используемый показатель в науке, технике и торговле во всем мире, и его часто просто называют килограмм в повседневной речи.

Килограмм был первоначально определен в 1795 году как масса одного человека. литр из воды. Это было простое определение, но его трудно было использовать на практике. Однако, согласно последним определениям единицы, точность этого отношения все еще составляет 30 ppm. В 1799 году платина Килограмм архива заменил его как эталон массы. В 1889 году цилиндр из платино-иридиевый, то Международный прототип килограмма (IPK) стал эталоном единицы массы в метрической системе и оставался им до 2019 года.[1] Килограмм был последней единицей СИ, определяемой физическим артефактом.

Килограмм теперь определяется с помощью секунды и метра на основе фиксированных фундаментальных констант природы.[2] Это позволяет правильно оборудовать метрология лаборатории для калибровки прибора для измерения массы, такого как Кормовой баланс в качестве первичного эталона для определения точной массы в килограммах, хотя IPK и другие точные килограммовые массы продолжают использоваться в качестве вторичных эталонов для всех обычных целей.

Определение

Килограмм определяется тремя фундаментальными физическими константами: скорость света c, конкретная частота атомного перехода ΔνCS, а Постоянная Планка час. В формальное определение является:

Килограмм (символ кг) - это единица массы в системе СИ. Он определяется как фиксированное числовое значение постоянной Планка. час быть 6.62607015×10−34 при выражении в единицах Дж⋅с, что равно кг⋅м2⋅s−1, где метр и второй определены в терминах c и ΔνCS.[3][4]

Это определение делает килограмм совместимым со старыми определениями: масса остается в пределах 30 промилле массы одного литра воды.[5]

Хронология предыдущих определений

Реплика Международный прототип килограмма на выставке в Cité des Sciences et de l'Industrie с двойным защитным стеклянным колпаком. До 2019 года ИПК служил основным эталоном килограмма.
  • 1793: могила (предшественник килограмма) определяется как масса 1 литр (дм3) воды, которая составила 18841 гран.[6]
  • 1795: грамм (1/1000 килограмма) была условно определена как масса одного кубического сантиметр воды при температуре плавления льда.[7]
  • 1799: Килограмм архива изготовлен как прототип
  • 1875–1889: Метр Соглашение подписан в 1875 году, что привело к созданию Международного прототипа килограмма (IPK) в 1879 году и его принятию на вооружение в 1889 году. Он имел массу, равную массе 1 дм3 воды при атмосферном давлении и температуре ее максимальной плотности, которая составляет примерно 4° C.
  • 2019: Килограмм на данный момент переопределенный с точки зрения Постоянная Планка как утверждено Генеральная конференция по мерам и весам (CGPM) 16 ноября 2018 г.

Название и терминология

Килограмм - единственная базовая единица СИ с Префикс SI (килограмм) как часть его названия. Слово килограмм или же килограмм происходит из Французский килограмм,[8] который сам по себе был ученой монетой, с префиксом Греческий основа χίλιοι хилиой "тысяча" до грамма, позднелатинский термин для обозначения «небольшого веса», происходящий от греческого γράμμα.[9] Слово килограмм было записано во французское право в 1795 г. Указ 18 Жерминаль,[10]который пересмотрел временную систему единиц, введенную французским Национальное собрание двумя годами ранее, когда могила был определен как вес (поиды) кубического сантиметра воды, равного 1/1000 могила.[11] В указе 1795 г. срок грамм таким образом заменил могила, и килограмм заменены могила.

Французское написание было принято в Великобритании, когда это слово впервые было использовано в английском языке в 1795 году.[12][8] с написанием килограмм принимается в Соединенных Штатах. В Соединенном Королевстве используются оба варианта написания, причем слово «килограмм» стало гораздо более распространенным.[13] Закон Великобритании, регулирующий единицы, которые будут использоваться при торговля по весу или мерке не препятствует использованию любого написания.[14]

В 19 веке французское слово килограмм, а сокращение из килограмм, был импортирован на английский язык, где он использовался для обозначения как килограмм[15] и километр.[16] Пока килограмм в качестве альтернативы приемлемо, чтобы Экономист Например,[17] канадское правительство Termium Plus В системе указано, что «использование СИ (Международной системы единиц) в научных и технических письмах» не позволяет его использовать, и это описано как «общепринятое неофициальное название» в Словаре единиц измерения Расса Роулетта.[18][19] Когда Конгресс США придал метрической системе правовой статус в 1866 году, это позволило использовать слово килограмм как альтернатива слову килограмм,[20] но в 1990 году отменил статус слова килограмм.[21]

Система SI была введена в 1960 г., а в 1970 г. BIPM начал публикацию Брошюра SI, который содержит все соответствующие решения и рекомендации CGPM по поводу агрегатов. В Брошюра SI заявляет, что «Недопустимо использовать сокращения для обозначений единиц измерения или названий единиц ...».[22][Заметка 2]

Килограмм становится базовой единицей: роль единиц для электромагнетизма

Как это часто бывает, в основном из-за единиц для электромагнетизма килограмм, а не грамм, в конечном итоге был принят в качестве базовой единицы массы в СИ. Соответствующая серия обсуждений и решений началась примерно в 1850-х годах и фактически завершилась в 1946 году. Вкратце, к концу 19 века «практические единицы» для электрических и магнитных величин, такие как ампер и вольт хорошо зарекомендовали себя в практическом использовании (например, для телеграфии). К сожалению, они не были последовательный с преобладающими в то время основными единицами измерения длины и массы, сантиметра и грамма. Однако «практические единицы» также включали некоторые чисто механические единицы; в частности, произведение ампера на вольт дает чисто механическую единицу измерения мощность, то ватт. Было замечено, что чисто механические практические единицы, такие как ватт, будут согласованы в системе, в которой базовой единицей длины является метр, а базовой единицей массы - килограмм. Фактически, учитывая, что никто не хотел заменять секунду как базовую единицу времени, метр и килограмм являются Только пара базовых единиц длины и массы, такая, что 1. ватт - это когерентная единица мощности, 2. базовые единицы длины и времени - это отношения целого числа в степени десяти к метру и грамму (так что система остается «метрической»), и 3. размеры базовых единиц длины и массы удобны для практического использования.[Заметка 3] При этом по-прежнему не учитываются чисто электрические и магнитные единицы: в то время как чисто механические практические единицы, такие как ватт, согласованы в системе метр-килограмм-секунда, явно электрические и магнитные единицы, такие как вольт, ампер и т. нет.[Примечание 5] Единственный способ также сделать те единиц, согласованных с системой метр-килограмм-секунда, должна модифицировать эту систему другим способом: нужно увеличить количество основных измерений с трех (длина, масса и время) до четырех (предыдущие три, плюс один чисто электрический один).[Примечание 6]

Состояние устройств электромагнетизма в конце XIX века.

Во второй половине XIX века система единиц сантиметр – грамм – секунда получил широкое признание для научной работы, лечения грамм как основная единица массы и килограмм как десятичное число, кратное базовой единице, образованной с помощью префикса метрики. Однако по мере того, как столетие подходило к концу, было повсеместное недовольство состоянием единиц электричества и магнетизма в системе CGS. Для начала было два очевидных варианта абсолютных единиц.[Примечание 7] электромагнетизма: «Электростатический» (CGS-ESU) и «Электромагнитный» (CGS-EMU) система. Но главная проблема заключалась в том, что размеры последовательный электрические и магнитные блоки были неудобны в либо этих систем; например, подразделение ESU электрическое сопротивление, который позже был назван статом, соответствует примерно 9×1011 ом, а блок ЭВС, впоследствии названный abohm, соответствует 10−9 ом.[Примечание 8]

Чтобы обойти эту трудность, в третьих введен комплект агрегатов: так называемый практические единицы. Практические единицы были получены как десятичные числа, кратные когерентным единицам CGS-EMU, выбранным таким образом, чтобы полученные величины были удобны для практического использования и чтобы практические единицы были, насколько это возможно, согласованы друг с другом.[25] Практические блоки включали такие блоки, как вольт, то ампер, то ом, так далее.,[26][27] которые позже были включены в систему СИ и которые мы используем по сей день.[Примечание 9] Действительно, основная причина, по которой метр и килограмм позже были выбраны в качестве базовых единиц длины и массы, заключалась в том, что они являются единственной комбинацией десятичных кратных или частичных кратных от метра и грамма разумного размера, которая может быть получена любым способом. согласованы с вольтом, ампером и т. д.

Причина в том, что электрические величины нельзя отделить от механических и тепловых: они связаны такими отношениями, как ток × разность электрических потенциалов = мощность. По этой причине практическая система также включала когерентные единицы для определенных механических величин. Например, предыдущее уравнение подразумевает, что ампер × вольт - это когерентная производная практическая единица мощности;[Примечание 10] это подразделение было названо ватт. Тогда когерентной единицей энергии является ватт, умноженный на секунду, который был назван джоуль. Джоуль и ватт также имеют удобные величины и являются десятичными числами, кратными когерентным единицам CGS для энергии ( эрг ) и мощности (эрг в секунду). Ватт не связан с системой сантиметр-грамм-секунда, но он является согласованы в системе метр-килограмм-секунда - и ни в какой другой системе, чьи основные единицы длины и массы являются десятичными кратными или частичными от метра и грамма разумного размера.

Однако, в отличие от ватта и джоуля, явно электрические и магнитные единицы (вольт, ампер ...) не согласованы даже в (абсолютной трехмерной) системе метр-килограмм-секунда. Действительно, можно понять, какими должны быть базовые единицы длины и массы, чтобы все практические единицы измерения должны быть согласованными (ватт и джоуль, а также вольт, ампер и т. д.). Ценности 107 метры (половина меридиана Земли, называемая квадрант) и 10−11 граммы (называется одиннадцатый грамм[Примечание 11]).[Примечание 13]

Следовательно, полная абсолютная система единиц, в которой практические электрические единицы согласованы, является квадрант – одиннадцатый грамм – секунда (QES) система. Однако крайне неудобные размеры базовых единиц по длине и массе сделали так, что никто всерьез не рассматривал возможность принятия системы QES. Таким образом, люди, работающие над практическим применением электричества, должны были использовать единицы для электрических величин, а также для энергии и мощности, которые не были согласованы с единицами, которые они использовали, например длина, масса и сила.

Между тем, ученые разработали еще одну полностью согласованную абсолютную систему, которую назвали Гауссова система, в котором единицы для чисто электрических величин взяты из CGE-ESU, а единицы для магнитных величин взяты из CGS-EMU. Эта система оказалась очень удобной для научной работы и до сих пор широко используется. Однако размеры его подразделений оставались либо слишком большими, либо слишком маленькими - многие порядки величины - для практических приложений.

Наконец, помимо всего этого, как в CGS-ESU, так и в CGS-EMU, а также в гауссовой системе, Уравнения Максвелла находятся "Нерационализированный", что означает, что они содержат различные факторы 4π что многим работникам было неудобно. Поэтому была разработана еще одна система, чтобы исправить это: «рационализированная» гауссова система, обычно называемая Система Лоренца – Хевисайда. Эта система до сих пор используется в некоторых областях физики. Однако единицы в этой системе связаны с гауссовыми единицами с коэффициентом √4π ≈ 3.5, что означает, что их величины оставались, как и величины гауссовых единиц, слишком большими или слишком маленькими для практических приложений.

Предложение Георгия

В 1901 г. Джованни Джорджи предложил новую систему единиц, которая исправила бы такое положение дел.[28] Он отметил, что механические практические единицы, такие как джоуль и ватт, согласованы не только в системе QES, но и в системе метр-килограмм-секунда (MKS).[29][Примечание 14] Конечно, было известно, что простое принятие метра и килограмма в качестве основных единиц - получение трехмерной системы MKS - не решит проблему: в то время как ватт и джоуль будут согласованы, это не будет так для вольта, ампер, ом и остальные практические единицы для электрических и магнитных величин (единственная трехмерная абсолютная система, в которой все практические единицы согласованы - это система QES).

Но Георгий указал, что вольт и остальное может быть сделали когерентным, если отказаться от идеи, что все физические величины должны быть выражены в терминах длины, массы и времени, и допустить четвертое базовое измерение для электрических величин. В качестве новой основной единицы можно выбрать любую практическую электрическую единицу, независимую от счетчика, килограмма и секунды. Вероятные кандидаты в четвертую независимую единицу включали кулон, ампер, вольт и ом, но в конечном итоге ампер оказался наиболее удобным с точки зрения метрологии. Более того, свобода, полученная благодаря тому, что электрическая единица независима от механической, может быть использована для рационализации уравнений Максвелла.

Идея о том, что следует отказаться от чисто «абсолютной» системы (т.е. системы, в которой основными измерениями являются только длина, масса и время), была отходом от точки зрения, которая, казалось, лежала в основе ранних прорывов Гаусс и Вебер (особенно их знаменитые «абсолютные измерения» магнитного поля Земли[30]:54–56), и научному сообществу потребовалось некоторое время, чтобы принять его - не в последнюю очередь потому, что многие ученые придерживались представления о том, что измерения величины в терминах длины, массы и времени так или иначе определяют ее «фундаментальную физическую природу».[31]:24, 26[29]

Принятие системы Георгия, ведущее к системе MKSA и SI

К 1920-м годам размерный анализ стал намного лучше понят[29] и становилось общепризнанным, что выбор как количества, так и идентичности основных измерений должен быть продиктован только удобством и что нет ничего действительно фундаментального в размерностях величины.[31] В 1935 году предложение Георгия было принято IEC как Система Георгия. Именно эту систему с тех пор называют Система МКС,[32]хотя «MKSA» используется осторожно. В 1946 г. CIPM одобрил предложение о принятии ампер в качестве электромагнитного блока системы «МКСА».[33]:109,110 В 1948 г. CGPM поручил CIPM «дать рекомендации по единой практической системе единиц измерения, пригодной для принятия всеми странами, присоединившимися к Метрической конвенции».[34] Это привело к запуску SI в 1960 году.

Подводя итог, можно сказать, что основной причиной, по которой килограмм был выбран в качестве базовой единицы массы вместо грамма, была, одним словом, вольт-ампер. А именно, комбинация метра и килограмма была единственным выбором основных единиц длины и массы, так что 1. вольт-ампер, который также называется ваттом и который является единицей мощности в практической системе электрических единиц. —Согласован, 2. основные единицы длины и массы являются десятичными кратными или долями метра и грамма, и 3. основные единицы длины и массы имеют удобные размеры.

Системы CGS и MKS сосуществовали на протяжении большей части периода с начала до середины 20-го века, но в результате решения принять «систему Георгия» в качестве международной системы единиц в 1960 году, килограмм теперь является Базовая единица СИ для массы, а определение грамма происходит от килограмма.

Переопределение на основе фундаментальных констант

В Система СИ после переопределения 2019 года: килограмм теперь фиксируется с точки зрения второй, то скорость света и Постоянная Планка; кроме того ампер больше не зависит от килограмма
А Кормовой баланс, который изначально использовался для измерения Постоянная Планка Что касается IPK, теперь его можно использовать для калибровки вторичных стандартных гирь для практического использования.
Основные статьи: 2019 новое определение базовых единиц СИ и CODATA 2018

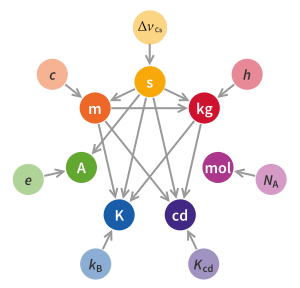
Замена Международного прототипа килограмма в качестве основного стандарта была мотивирована свидетельствами, накопленными в течение длительного периода времени, что масса IPK и его реплик менялась; IPK отличался от своих реплик примерно на 50 микрограммов с момента их производства в конце XIX века. Это привело к несколько конкурирующих усилий разработать технологию измерения, достаточно точную, чтобы гарантировать замену артефакта в килограммах определением, основанным непосредственно на физических фундаментальных константах.[1] Физические стандартные массы, такие как IPK и его копии, по-прежнему служат вторичными стандартами.

Международный комитет мер и весов (CIPM) утвердил переопределение основных единиц СИ в ноябре 2018 года, который определяет килограмм, определяя Постоянная Планка быть точно 6.62607015×10−34 кг⋅м2⋅s−1, эффективно определяя килограмм через секунды и метр. Новое определение вступило в силу 20 мая 2019 года.[1][3][35]

До переопределения килограмм и несколько других единиц СИ, основанных на килограмме, определялись искусственным металлическим артефактом: Килограмм архива с 1799 по 1889 год, а Международный прототип килограмма с 1889 г.[1]

В 1960 г. метр, ранее аналогичным образом определявшийся со ссылкой на один платино-иридиевый слиток с двумя отметками на нем, был переопределен в терминах инвариантной физической константы (длина волны конкретного излучения света, излучаемого криптон,[36] а позже скорость света ), чтобы стандарт можно было независимо воспроизвести в разных лабораториях, следуя письменной спецификации.

На 94-м заседании Международный комитет мер и весов (CIPM) в 2005 г. рекомендовалось сделать то же самое с килограммом.[37]

В октябре 2010 г. CIPM проголосовал за внесение резолюции на рассмотрение в Генеральная конференция по мерам и весам (CGPM), чтобы «принять к сведению намерение» определить килограмм в терминах Постоянная Планка, час (который имеет размерность энергии, умноженной на время, таким образом, масса × длина2 / время) вместе с другими физическими константами.[38][39] Эта резолюция была принята 24-й конференцией CGPM.[40] в октябре 2011 г. и далее обсуждались на 25-й конференции в 2014 г.[41][42] Хотя Комитет признал, что был достигнут значительный прогресс, он пришел к выводу, что данные еще не представляются достаточно надежными для принятия пересмотренного определения и что работа должна продолжаться, чтобы обеспечить принятие на 26-м заседании, запланированном на 2018 год.[41] Такое определение теоретически позволило бы использовать любой прибор, способный определять килограмм в терминах постоянной Планка, при условии, что он обладает достаточной точностью, точностью и стабильностью. В Кормовой баланс - один из способов сделать это.

В рамках этого проекта множество очень разные технологии и подходы рассматривались и исследовались на протяжении многих лет. Некоторые из этих подходов были основаны на оборудовании и процедурах, которые позволили бы воспроизводимое производство новых прототипов килограммовой массы по запросу (хотя и с чрезвычайными усилиями) с использованием методов измерения и свойств материалов, которые в конечном итоге основаны на физических константах или прослеживаются к ним. Другие были основаны на устройствах, которые измеряли либо ускорение, либо вес настроенных вручную килограммовых контрольных масс и выражали их величины в электрических терминах с помощью специальных компонентов, которые позволяют прослеживать физические константы. Все подходы зависят от преобразования измерения веса в массу и, следовательно, требуют точного измерения силы тяжести в лабораториях. Все подходы точно фиксировали бы одну или несколько констант природы на определенном значении.

Кратные SI

Основная статья: Порядки величины (масса)

Потому что Префиксы SI не могут быть объединены (последовательно связаны) в имени или символе единицы измерения, с единицей измерения используются префиксы СИ грамм, нет килограмм, в названии которого уже есть префикс.[43] Например, одна миллионная килограмма равна 1 мг (один миллиграмм), а не 1 мкг (один микрокилограмм).

SI, кратные грамму (г)
ПодмножественныеКратные
ЦенитьСимвол SIИмяЦенитьСимвол SIИмя
10−1 граммdgдециграмм101 граммдагдекаграмма
10−2 граммcgсантиграмма102 граммhgгектограмм
10−3 грамммгмиллиграмм103 граммкгкилограмм
10−6 грамммкгмикрограмм106 граммMgмегаграмма (тонна)
10−9 граммнгнанограмм109 граммGgгигаграмма
10−12 граммpgпикограмма1012 граммTgтераграмма
10−15 граммфгфемтограмма1015 граммСтр.петаграмма
10−18 граммагаттограмма1018 граммНапримерэкзаграмма
10−21 граммzgзептограмма1021 граммZgзеттаграмма
10−24 граммygйоктограмма1024 граммYgйоттаграмма
Обычные единицы с префиксом выделены жирным шрифтом.[Примечание 15]
  • Микрограмм обычно обозначается аббревиатурой «мкг» на этикетках фармацевтических препаратов и пищевых добавок, чтобы избежать путаницы, поскольку префикс «μ» не всегда хорошо распознается за пределами технических дисциплин.[Примечание 16] (Выражение «mcg» также является символом устаревшего CGS единица измерения, известная как «миллицентиграмма», равная 10 мкг.)
  • В Соединенном Королевстве, поскольку из-за путаницы между миллиграммами и микрограммами при сокращении микрограммов были сделаны серьезные ошибки в лечении, в Шотландских рекомендациях по паллиативной помощи дана рекомендация: дозы менее одного миллиграмма должны быть выражены в микрограммах и слово микрограмм должно быть написано полностью, и что недопустимо использовать «мкг» или «мкг».[44]
  • Гектограмм (100 г) - это очень часто используемая единица измерения в розничной торговле продуктами питания в Италии, обычно называемая единицей измерения. этто, Короче для эттограммаИтальянский гектограмм.[45][46][47]
  • Прежнее стандартное написание и аббревиатуры «дека-» и «дк» привели к появлению таких сокращений, как «дкм» (декаметр) и «дкг» (декаграмма).[48] По состоянию на 2020 год аббревиатура «dkg» (10 г) до сих пор используется в некоторых частях Центральной Европы в розничной торговле для некоторых пищевых продуктов, таких как сыр и мясо, например здесь:.[49][50][51][52][53]
  • Название объекта мегаграмма используется редко, и даже тогда обычно только в технических областях в контекстах, где требуется особенно строгое соответствие стандарту SI. В большинстве случаев имя тонна вместо этого используется. Тонна и ее символ «t» были приняты CIPM в 1879 году. Это внесистемная единица, принятая BIPM для использования с SI. Согласно BIPM, «эту единицу иногда называют« метрической тонной »в некоторых англоязычных странах».[54] Название объекта мегатонна или же мегатонна (Mt) часто используется в специальной литературе по парниковый газ выбросов, в то время как эквивалентная единица измерения в научных статьях по этому вопросу часто - тераграмма (Тг).

Смотрите также

Примечания

  1. ^ Фунт энирдупуа является частью обоих Обычная система единиц США и Имперская система единиц. это определяется как точно 0.45359237 килограммы.
  2. ^ Французский текст (который является авторитетным текстом) гласит: "Не было авторизованных средств использования аббревиатур для символов и названий единиц ..."
  3. ^ Покажем, что если известно, что метр и килограмм удовлетворяют всем трем условиям, то другого выбора нет. Когерентная единица мощности, записанная в базовых единицах длины, массы и времени, равна (базовая единица массы) × (базовая единица длины).2/ (базовая единица времени)3. Утверждается, что ватт соответствует системе метр-килограмм-секунда; таким образом, 1 ватт = (1 кг) × (1 мес.)2/(1 с)3. Второй остается как есть, и отмечается, что если базовая единица длины изменяется на L м а базовая единица массы - M кг, то когерентная единица мощности (M кг) × (L м)2/(1 с)3 = ML2 × (1 кг) × (1 мес.)2/(1 с)3 = ML2 ватт. Поскольку основные единицы длины и массы таковы, что когерентной единицей мощности является ватт, мы требуем, чтобы ML2 = 1. Отсюда следует, что если мы изменим базовую единицу длины в раз L, то мы должны изменить базовую единицу массы в раз 1/L2 если ватт должен оставаться согласованной единицей. Было бы непрактично делать базовую единицу длины десятичной. несколько метра (10 м, 100 м, или больше). Поэтому наш единственный вариант - сделать базовую единицу длины десятичной. частичный метра. Это означало бы уменьшение метр с коэффициентом 10 чтобы получить дециметр (0,1 м), или в раз 100 чтобы получить сантиметр, или с коэффициентом 1000 чтобы получить миллиметр. Уменьшение базовой единицы длины было бы непрактичным (например, следующий десятичный множитель, 10000, даст базовую единицу длины в одну десятую миллиметра), поэтому эти три фактора (10, 100, и 1000) являются единственно допустимыми вариантами в пределах базовой единицы длины. Но тогда базовая единица массы должна быть больше чем килограмм, по следующим факторам: 102 = 100, 1002 = 10000, и 10002 = 106. Другими словами, ватт - это связная единица для следующих пар основных единиц длины и массы: 0,1 м и 100 кг, 1 см и 10000 кг, и 1 мм и 1000000 кг. Даже в первой паре базовая единица массы непрактично велика, 100 кг, а по мере уменьшения базовой единицы длины базовая единица массы становится еще больше. Таким образом, если предположить, что секунда остается базовой единицей времени, комбинация метр-килограмм является единственной такой, что базовые единицы для длины и массы не являются ни слишком большими, ни слишком маленькими, и так, чтобы они были десятичными кратными или делениями метра и грамма, и так что ватт является когерентной единицей.
  4. ^ Система, в которой основными величинами являются длина, масса и время, и Только эти трое.
  5. ^ Мы увидим, что существует только одна трехмерная «абсолютная» система.[Примечание 4] в котором все практические единицы согласованы, включая вольт, ампер и т. д .: единица, в которой базовая единица длины 107 м а базовая единица массы - 10−11 грамм. Ясно, что такие величины непрактичны.
  6. ^ Между тем, параллельно происходили разработки, которые, по независимым причинам, в конечном итоге привели к трем дополнительным фундаментальным измерениям, всего семь: измерения температуры, интенсивность света, а количество вещества.
  7. ^ То есть единицы, которые имеют длину, массу и время в качестве основных измерений и которые последовательный в системе CGS.
  8. ^ Довольно долгое время подразделения ESU и EMU не имели особых названий; можно было бы просто сказать, например блок сопротивления ESU. По-видимому, только в 1903 г. А. Э. Кеннелли предложил, чтобы названия единиц EMU были получены путем добавления к названию соответствующей «практической единицы» префикса «ab-» (сокращение от «absolute», дающее «abohm», «упасть ","буйствовать »И т. Д.), И чтобы названия единиц ESU были получены аналогичным образом с использованием префикса« abstat- », который позже был сокращен до« stat- »(что дает« statohm »,«статвольт ’, ‘статампер ', так далее.).[23]:534–5 Эта система именования широко использовалась в США, но, по-видимому, не в Европе.[24]
  9. ^ Использование электрических единиц СИ является по существу универсальным во всем мире (помимо явно электрических единиц, таких как ом, вольт и ампер, также почти универсально использовать ватт при конкретной количественной оценке. электрические мощность). Так обстоит дело даже в Соединенных Штатах и ​​Соединенном Королевстве, двух известных странах, которые входят в небольшую группу стран, которые в той или иной степени продолжают сопротивляться широкое внутреннее внедрение системы СИ. Но сопротивление принятию единиц СИ в основном касается механических единиц (длина, масса, сила, крутящий момент, давление), тепловых единиц (температура, тепло) и единиц для описания. ионизирующего излучения (активность радионуклида, поглощенная доза, эквивалент дозы); это не касается электрических блоков.
  10. ^ В переменный ток (AC) схемы можно ввести три вида власти: активный, реактивный и кажущийся. Хотя все три имеют одинаковые размеры и, следовательно, одни и те же единицы измерения, когда они выражаются в базовых единицах (например, кг⋅м2⋅s-3), для каждого принято использовать разные названия: соответственно ватт, вольт-амперный реактивный, а вольт-ампер.
  11. ^ В то время было популярно обозначать десятичные и дробные части величин с помощью системы, предложенной Дж. Дж. Стони. Систему проще всего объяснить на примерах. Для десятичных кратных: 109 граммы будет обозначаться как грамм девять, 1013 м будет метр-тринадцатьи т. д. Для подмножителей: 10−9 граммы будет обозначаться как девятый грамм, 10−13 м будет тринадцатый метри т. д. Система также работала с единицами измерения, в которых использовались метрические префиксы, например, 1015 сантиметр было бы сантиметр пятнадцать. Правило, когда оно прописано, таково: мы обозначаем показатель степени 10, который служит множителем, добавленным кардинальным числом, если показатель положительный, и порядковым числом с префиксом, если показатель степени отрицательным. . '[26]
  12. ^ Это также очевидно из того факта, что как в абсолютных, так и в практических единицах ток - это заряд за единицу времени, так что единица времени - это единица заряда, деленная на единицу тока. В практической системе мы знаем, что базовой единицей времени является секунда, поэтому кулон на ампер дает секунду. Базовая единица времени в CGS-EMU - это абкулон на один ампер, но это отношение такое же, как кулон на ампер, поскольку единицы тока и заряда используют один и тот же коэффициент преобразования, 0.1, для перехода между EMU и практическими единицами (кулон / ампер = (0,1 абкулон)/(0,1 ампера) = абкулон / абампер). Таким образом, базовой единицей времени в EMU также является секунда.
  13. ^ Это можно показать из определений, скажем, вольта, ампера и кулона в единицах EMU. Вольт был выбран как 108 ЕВС (абвольты ), ампер как 0.1 ЕВС (шумит ), а кулон - как 0.1 ЕВС (abcoulombs ). Теперь мы используем тот факт, что при выражении в базовых единицах CGS abvolt равен грамм1/2·см3/2/ с2, абампер грамм1/2·см1/2/ с, а абкулон грамм1/2·см1/2. Предположим, мы выбрали новые базовые единицы длины, массы и времени, равные L сантиметры, M граммы и Т секунд. Тогда вместо абвольта единицей электрического потенциала будет (M × г)1/2·(L × см)3/2/(Т × с)2 = M1/2L3/2/Т2 × г1/2·см3/2/ с2 = M1/2L3/2/Т2 абвольты. Мы хотим, чтобы это новое устройство было вольт, поэтому мы должны иметь M1/2L3/2/Т2 = 108. Аналогично, если мы хотим, чтобы новой единицей измерения тока был ампер, мы получаем, что M1/2L1/2/Т = 0.1, и если мы хотим, чтобы новой единицей заряда был кулон, мы получаем, что M1/2L1/2 = 0.1. Это система трех уравнений с тремя неизвестными. Разделив среднее уравнение на последнее, мы получим Т = 1, поэтому секунда должна оставаться базовой единицей времени.[Примечание 12] Если затем разделить первое уравнение на среднее (и использовать тот факт, что Т = 1), получаем, что L = 108/0.1 = 109, поэтому базовая единица длины должна быть 109 см = 107 м. Наконец, возводим окончательное уравнение в квадрат и получаем, что M = 0.12/L = 10−11, поэтому базовая единица массы должна быть 10−11 граммы.
  14. ^ Чтобы убедиться в этом, сначала отметим, что размеры энергии равны ML2/Т2 и власти, ML2/Т3. Одно из значений этих размерных формул состоит в том, что если единица массы изменяется в раз M, единица длины в раз L, а единицу времени - в раз Т, то единица энергии изменится в раз ML2/Т2 и единицы мощности в раз ML2/Т3. Это означает, что если уменьшить единицу длины и в то же время увеличить единицу массы таким образом, чтобы продукт ML2 остается постоянным, единицы энергии и мощности не изменяются. Ясно, что это произойдет, если M = 1/L2. Теперь мы знаем, что ватт и джоуль согласованы в системе, в которой базовая единица длины равна 107 м в то время как базовая единица массы 10−11 граммы. Мы только что узнали, что тогда они также будут согласованы в любой системе, в которой базовой единицей длины является L × 107 м а базовая единица массы - 1/L2 × 10−11 грамм, куда L - любое положительное действительное число. Если мы установим L = 10−7, мы получаем метр как базовую единицу длины. Тогда соответствующая базовая единица массы оказывается 1/(10−7)2 × 10−11 грамм=1014 × 10−11 грамм = 103 грамм = 1 кг.
  15. ^ Критерий: в сумме не менее пяти вхождений на Британский национальный корпус и Корпус современного американского английского, включая как единственное, так и множественное число для -грамм и -грамм написание.
  16. ^ Практика использования аббревиатуры «мкг», а не символа СИ «мкг» была официально разрешена в США для практикующих врачей в 2004 г. Совместная комиссия по аккредитации организаций здравоохранения (JCAHO) в своих Список «Не использовать»: сокращения, акронимы и символы потому что «мкг» и «мг», написанные от руки, можно перепутать друг с другом, что приведет к тысячекратной передозировке (или недостаточной дозировке). Мандат был также принят Институт безопасных методов лечения.

Рекомендации

  1. ^ а б c d Резник, Брайан (20 мая 2019 г.). «Новый килограмм только что дебютировал. Это огромное достижение». vox.com. Получено 23 мая, 2019.
  2. ^ «Последнее: изменение отметки в килограммах одобрено». AP Новости. Ассошиэйтед Пресс. 16 ноября 2018 г.. Получено 4 марта, 2020.
  3. ^ а б Проект Резолюции А «О пересмотре Международной системы единиц (СИ)» для представления ГКБМ на его 26-м заседании (2018 г.) (PDF)
  4. ^ Решение CIPM / 105-13 (октябрь 2016 г.). Сегодня 144-я годовщина Метр Соглашение.
  5. ^ Плотность воды 0,999972 г / см3 при 3,984 ° C. Видеть Франк, Феликс (2012). Физика и физическая химия воды. Springer. ISBN  978-1-4684-8334-5.
  6. ^ Guyton; Лавуазье; Monge; Бертолле; и другие. (1792). Annales de chimie ou Recueil de mémoires, касающихся химии и искусства, qui en dependent. 15-16. Париж: Chez Joseph de Boffe. п. 277.
  7. ^ Gramme, le poids absolu d'un volume d'eau pure égal au cube de la centième partie du mètre, et à la température de la glace fondante
  8. ^ а б "Килограмм". Оксфордский словарь английского языка. Oxford University Press. Получено 3 ноября, 2011.
  9. ^ Fowlers, HW; Фаулер, Ф.Г. (1964). Краткий оксфордский словарь. Оксфорд: Кларендон Пресс.Греческий γράμμα (как это было γράφ -μα, Дорический γράθμα) означает «что-то написанное, буква», но оно стало использоваться как единица веса, очевидно равная 1/24 из унция (1/288 из Весы, что соответствует примерно 1,14 грамму в современных единицах), когда-то в эпоху поздней античности. Французский грамм был заимствован из латыни грамма, сам по себе довольно неясный, но найденный в Carmen de ponderibus et mensuris (8.25) приписывается Реммиус Палаемон (эт. 1 век), где это вес двух Оболи (Чарльтон Т. Льюис, Чарльз Шорт, Латинский словарь s.v. "грамма", 1879) Генри Джордж Лидделл. Роберт Скотт. Греко-английский лексикон (переработанное и дополненное издание, Оксфорд, 1940 г.) s.v. γράμμα, ссылаясь на работы 10 века Геопоника и папирус 4-го века, изданный Л. Миттеисом, Griechische Urkunden der Papyrussammlung zu Leipzig, т. я (1906), 62 II 27.
  10. ^ "Décret relatif aux poids et aux mesures du 18 germinal an 3 (7 апреля 1795 г.)" [Указ 18 Жерминала III года (7 апреля 1795 г.) о мерах и весах]. Grandes Lois de la République (На французском). Digithèque de matériaux juridiques et politiques, Университет Перпиньяна. Получено 3 ноября, 2011.
  11. ^ Национальный конгресс, décret du 1э août 1793, изд. Дюверже, Полная коллекция законов, декретов, постановлений, официальных правил Лувра, publiée sur les éditions officielles du Louvre, т. 6 (2-е изд. 1834 г.), п. 70. метр (mètre), от которого зависит это определение, само определялось как десятимиллионная часть четверти земного меридиан, приведены в традиционные единицы как 3 пестрые, 11.44 Lignes (а Ligne будучи 12-й частью мешок (дюйм), или 144 часть пестрый.
  12. ^ Пельтье, Жан-Габриэль (1795). "Париж в 1795 году". Ежемесячный обзор. 17: 556. Получено 2 августа, 2018. Современный английский перевод французского указа 1795 г.
  13. ^ "Килограмм". Оксфордские словари. Архивировано из оригинал 31 января 2013 г.. Получено 3 ноября, 2011.
  14. ^ "Правописание слова" грамм "и т. Д.". Закон о мерах и весах 1985 года. Канцелярия Ее Величества. 30 октября 1985 г.. Получено 6 ноября, 2011.
  15. ^ "килограмм (n1)". Оксфордский словарь английского языка (2-е изд.). Оксфорд: Издательство Оксфордского университета. 1989 г.. Получено 8 ноября, 2011.
  16. ^ "килограмм (n2)". Оксфордский словарь английского языка (2-е изд.). Оксфорд: Издательство Оксфордского университета. 1989 г.. Получено 8 ноября, 2011.
  17. ^ "Гид по стилю" (PDF). Экономист. 7 января 2002 г. Архивировано с оригинал (PDF) 1 июля 2017 г.. Получено 8 ноября, 2011.
  18. ^ «килограмм, кг, килограмм». Termium Plus. Правительство Канады. 8 октября 2009 г.. Получено 29 мая, 2019.
  19. ^ "килограмм". Как много?. Архивировано из оригинал 16 ноября 2011 г.. Получено 6 ноября, 2011.
  20. ^ 29-й Конгресс США, сессия 1 (13 мая 1866 г.). "HR 596, Закон, разрешающий использование метрической системы мер и весов". Архивировано из оригинал 5 июля 2015 г.
  21. ^ «Метрическая система измерения: интерпретация международной системы единиц для Соединенных Штатов Америки; уведомление» (PDF). Федеральный регистр. 63 (144): 40340. 28 июля 1998 г. Архивировано с оригинал (PDF) 15 октября 2011 г.. Получено 10 ноября, 2011. Устаревшие единицы Как указано в уведомлении Федерального реестра 1990 г., ...
  22. ^ Международное бюро мер и весов (2006), Международная система единиц (СИ) (PDF) (8-е изд.), С. 130, ISBN  92-822-2213-6, в архиве (PDF) с оригинала 14 августа 2017 г.
  23. ^ Кеннелли, А.Э. (Июль 1903 г.). «Магнитные устройства и другие предметы, которые могут привлечь внимание на следующем международном электрическом конгрессе». Труды Американского института инженеров-электриков. XXII: 529–536. Дои:10.1109 / T-AIEE.1903.4764390. S2CID  51634810. [п. 534] Напрашивается способ прикрепления приставки ab или же пресс в практическую единицу или Q.E.S. единицу, чтобы выразить абсолютную или соответствующую магнитную единицу C.G.S. … [п. 535] Во всеобъемлющей системе электромагнитной терминологии электрические блоки C.G.S. также должны быть названы. Иногда они упоминаются в электротехнических документах, но всегда в извиняющейся, символической манере из-за отсутствия имен, прикрывающих их наготу. Их можно обозначать префиксом воздерживаться.
  24. ^ Силсби, Фрэнсис (апрель – июнь 1962 г.). «Системы электроустановок». Журнал исследований Национального бюро стандартов Раздел C. 66C (2): 137–183. Дои:10.6028 / jres.066C.014.
  25. ^ «Единицы, физические». Британская энциклопедия. 27 (11-е изд.). Нью-Йорк: Британская энциклопедия. 1911. с. 740.
  26. ^ а б Томсон, сэр У .; Foster, C.G .; Maxwell, J.C .; Stoney, G.J .; Дженкин, Флиминг; Сименс; Bramwell, F.J .; Эверетт (1873 г.). Отчет о 43-м заседании Британской ассоциации содействия развитию науки. Брэдфорд. п. 223.
  27. ^ "Электрический Конгресс". Электрик. 7: 297. 24 сентября 1881 г.. Получено 3 июня, 2020.
  28. ^ Джованни Джорджи (1901), «Разумные единицы электромагнитного поля», Atti della Associazione Elettrotecnica Italiana (на итальянском языке), Турин, ПР  18571144MДжованни Джорджи (1902), Рациональные единицы электромагнетизма Оригинальная рукопись с рукописными пометками Оливера Хевисайда
  29. ^ а б c Джорджи, Джованни (2018) [Первоначально опубликовано в июне 1934 г. центральным офисом Международная электротехническая комиссия (IEC), Лондон, для Консультативного комитета IEC № 1 по номенклатуре, Раздел B: Электрические и магнитные величины и единицы.]. «Меморандум о системе практических единиц M.K.S.». Письма IEEE Magnetics. 9: 1–6. Дои:10.1109 / LMAG.2018.2859658.
  30. ^ Каррон, Нил (2015). "Вавилон единиц. Эволюция систем единиц в классическом электромагнетизме". arXiv:1506.01951 [Physics.hist-ph ].
  31. ^ а б Бриджмен, П.В. (1922). Размерный анализ. Издательство Йельского университета.
  32. ^ Артур Э. Кеннелли (1935), «Принятие Абсолютной системы практических единиц метр – килограмм – масса – секунда (M.K.S.) Международной электротехнической комиссией (I.E.C.), Брюссель, июнь 1935 г.», Труды Национальной академии наук Соединенных Штатов Америки, 21 (10): 579–583, Bibcode:1935ПНАС ... 21..579К, Дои:10.1073 / pnas.21.10.579, ЧВК  1076662, PMID  16577693
  33. ^ Международное бюро мер и весов (2006), Международная система единиц (СИ) (PDF) (8-е изд.), ISBN  92-822-2213-6, в архиве (PDF) с оригинала 14 августа 2017 г.
  34. ^ Резолюция 6 - Предложение по созданию практической системы единиц измерения. Девятая Генеральная конференция поид и мер (CGPM). 12–21 октября 1948 г.. Получено 8 мая, 2011.
  35. ^ Паллаб Гош (16 ноября 2018 г.). «Килограмм получает новое определение». Новости BBC. Получено 16 ноября, 2018.
  36. ^ Международное бюро мер и весов (2006), Международная система единиц (СИ) (PDF) (8-е изд.), С. 112, ISBN  92-822-2213-6, в архиве (PDF) с оригинала 14 августа 2017 г.
  37. ^ Рекомендация 1: Подготовительные шаги к новым определениям килограмма, ампера, кельвина и моля с точки зрения фундаментальных констант. (PDF). 94-е заседание Международного комитета мер и весов. Октябрь 2005. с. 233. В архиве (PDF) с оригинала 30 июня 2007 г.. Получено 7 февраля, 2018.
  38. ^ «NIST поддерживает предложение по обновленной системе единиц измерения». Nist.gov. 26 октября 2010 г.. Получено 3 апреля, 2011.
  39. ^ Ян Миллс (29 сентября 2010 г.). «Проект главы 2 брошюры СИ после переопределения базовых единиц» (PDF). CCU. Получено 1 января, 2011.
  40. ^ Резолюция 1 - О возможном будущем пересмотре Международной системы единиц СИ (PDF). 24-е заседание Генеральной конференции по мерам и весам. Севр, Франция. 17–21 октября 2011 г.. Получено 25 октября, 2011.
  41. ^ а б «МБМВ - Резолюция 1 25-го ГКБМ». www.bipm.org. Получено 27 марта, 2017.
  42. ^ «Генеральная конференция мер и весов одобряет возможные изменения в Международной системе единиц, в том числе новое определение килограмма» (PDF) (Пресс-релиз). Севр, Франция: Генеральная конференция по мерам и весам. 23 октября 2011 г.. Получено 25 октября, 2011.
  43. ^ BIPM: SI Brochure: Section 3.2, Килограмм
  44. ^ «Информация о назначении жидких лекарственных средств». Руководство Шотландии по паллиативной помощи. Архивировано из оригинал 10 июля 2018 г.. Получено 15 июня, 2015.
  45. ^ Том Стобарт, Энциклопедия Кука, 1981, с. 525
  46. ^ J.J. Киндер, В. Савини, Использование итальянского: руководство по современному использованию, 2004, ISBN  0521485568, п. 231
  47. ^ Джакомо Девото, Джан Карло Оли, Новый словарь, иллюстрирующий делла лингва итальянская, 1987, s.v. 'ètto': "partialissima nell'uso comune: un e. di caffè, un e. ди мортаделла; formaggio a 2000 lire l'etto"
  48. ^ Национальное бюро стандартов США, Международная метрическая система мер и весов, "Официальные сокращения международных метрических единиц", 1932 г., п. 13
  49. ^ "Jestřebická hovězí šunka 10 dkg | Rancherské speciality". eshop.rancherskespeciality.cz (на чешском языке). Архивировано из оригинал 16 июня 2020 г.. Получено 16 июня, 2020.
  50. ^ "Sedliacka šunka 1 dkg | Gazdovský dvor - Farma Busov Gaboltov". Седляцкая шунка 1 дкг (на словацком). Архивировано из оригинал 16 июня 2020 г.. Получено 16 июня, 2020.
  51. ^ "sýr bazalkový - Farmářské Trhy". www.e-farmarsketrhy.cz (на чешском языке). Архивировано из оригинал 16 июня 2020 г.. Получено 16 июня, 2020.
  52. ^ «Английское Меню - Кафе Mediterran». Архивировано из оригинал 16 июня 2020 г.. Получено 16 июня, 2020. Стейк из говядины 20 дкг; Стейк из говядины 40 дкг; Толстое тесто 35 дкг
  53. ^ "Termékek - Csíz Sajtműhely" (на венгерском). Архивировано из оригинал 16 июня 2020 г.. Получено 16 июня, 2020.
  54. ^ Единицы, не относящиеся к системе СИ, которые принимаются для использования с системой СИ, Брошюра SI: Раздел 4 (Таблица 8), МБМВ

внешняя ссылка

Внешние изображения
значок изображения BIPM: ИПК в трех вложенных колпаках
значок изображения NIST: K20, килограмм национального прототипа США опираясь на люминесцентную панель для яиц
значок изображения BIPM: Очистка паром прототипа весом 1 кг перед массовым сравнением
значок изображения BIPM: IPK и шесть его сестринских копий в их хранилище
значок изображения Возраст: Кремниевая сфера для проекта Авогадро
значок изображения НПЛ: Проект Watt Balance NPL
значок изображения NIST: этот конкретный Баланс Рюпрехта, точные весы австрийского производства, использовались NIST с 1945 по 1960 год.
значок изображения BIPM: Весы FB ‑ 2 изгиб-полоса, современные прецизионные весы BIPM со стандартным отклонением в одну десятимиллиардную килограмма (0,1 мкг)
значок изображения BIPM: Весы Mettler HK1000 с 1 разрешение мкг и 4 кг максимальная масса. Также используется лабораторией первичных стандартов NIST и Sandia National Laboratories.
значок изображения Micro-g LaCoste: Абсолютный гравиметр ФГ ‑ 5, (диаграмма ), используемый в национальных лабораториях для измерения силы тяжести до 2 мкГал точность

Ролики