Электропитание переменного тока - Википедия - AC power

Мгновенная мощность в электрической цепи - это скорость потока энергии через заданную точку цепи. В переменный ток схемы, элементы хранения энергии, такие как индукторы и конденсаторы может привести к периодическому изменению направления потока энергии.
Доля мощности, усредненная за полный цикл Форма волны переменного тока, приводит к чистой передаче энергии в одном направлении, известной как активная мощность (чаще называют Реальная власть во избежание двусмысленности, особенно при обсуждении нагрузок с несинусоидальными токами). Часть энергии за счет накопленной энергии, которая возвращается к источнику в каждом цикле, известна как мгновенная реактивная мощность, а его амплитуда - абсолютное значение реактивной мощности.
Активная, реактивная и полная мощность
В простой цепи переменного тока, состоящей из источника и линейной нагрузки, как ток, так и напряжение равны синусоидальный. Если нагрузка чисто резистивный, две величины меняют полярность одновременно. В любой момент произведение напряжения и тока положительно или равно нулю, в результате чего направление потока энергии не меняется. В этом случае передается только активная мощность.
Если нагрузка чисто реактивный, то напряжение и ток сдвинуты по фазе на 90 градусов. Для двух четвертей каждого цикла произведение напряжения и тока положительное, но для двух других кварталов произведение отрицательное, что указывает на то, что в среднем в нагрузку поступает ровно столько энергии, сколько возвращается обратно. В каждом полупериоде нет чистого потока энергии. В этом случае идет только реактивная мощность: нет чистой передачи энергии нагрузке; однако электрическая энергия течет по проводам и возвращается в обратном направлении по тем же самым проводам. Ток, необходимый для этого потока реактивной мощности, рассеивает энергию в сопротивлении линии, даже если идеальное нагрузочное устройство само не потребляет энергии. Практические нагрузки имеют сопротивление, а также индуктивность или емкость, поэтому как активная, так и реактивная мощность передаются на нормальные нагрузки.
Кажущаяся мощность - это продукт среднеквадратичное значение значения напряжения и тока. Полная мощность принимается во внимание при проектировании и эксплуатации энергосистем, поскольку, хотя ток, связанный с реактивной мощностью, не действует на нагрузку, он все равно должен подаваться от источника питания. Проводники, трансформаторы и генераторы должны иметь такой размер, чтобы выдерживать полный ток, а не только ток, который выполняет полезную работу. Отсутствие обеспечения достаточной реактивной мощности в электрических сетях может привести к снижению уровней напряжения и, при определенных условиях эксплуатации, к полному разрушению сети или затемнение. Другое следствие заключается в том, что сложение полной мощности для двух нагрузок не даст точной общей мощности, если у них нет одинаковой разности фаз между током и напряжением (одинаковой фактор силы ).
Обычно конденсаторы рассматриваются как генерирующие реактивную мощность, а катушки индуктивности - как если бы они ее потребляли. Если конденсатор и катушка индуктивности размещены параллельно, то токи, протекающие через конденсатор и катушку индуктивности, имеют тенденцию отменяться, а не складываться. Это основной механизм управления коэффициентом мощности при передаче электроэнергии; конденсаторы (или катушки индуктивности) вставляются в цепь для частичной компенсации реактивной мощности, «потребляемой» («генерируемой») нагрузкой. Чисто емкостные цепи обеспечивают реактивную мощность, при этом форма волны тока опережает форму волны напряжения на 90 градусов, в то время как чисто индуктивные цепи поглощают реактивную мощность, форма волны тока отстает от формы волны напряжения на 90 градусов. Результатом этого является то, что емкостные и индуктивные элементы схемы имеют тенденцию компенсировать друг друга.[1]
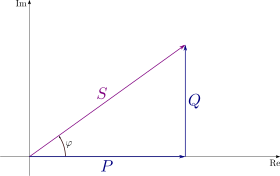
Комплексная мощность - это векторная сумма активной и реактивной мощности. Полная мощность - это величина комплексной мощности.
Активная мощность, п
Реактивная сила, Q
Комплексная мощность, S
Полная мощность, | S |
Фаза напряжения относительно тока,
Инженеры используют следующие термины для описания потока энергии в системе (и назначают каждому из них разные единицы, чтобы различать их):
- Активная мощность,[2] п, или же Реальная власть:[3] ватт (W);
- Реактивная сила, Q: вольт-амперный реактивный (var);
- Комплексная мощность, S: вольт-ампер (VA);
- Полная мощность, |S|: величина сложной мощности S: вольт-ампер (ВА);
- Фаза напряжения относительно тока, φ: угол разницы (в градусах) между током и напряжением; . Текущее запаздывающее напряжение (квадрант I вектор), текущее опережающее напряжение (вектор IV квадранта).
Все они обозначены на соседней диаграмме (называемой степенным треугольником).
На диаграмме п активная мощность, Q - реактивная мощность (в данном случае положительная), S комплексная мощность и длина S кажущаяся мощность. Реактивная мощность не работает, поэтому она представлена как мнимая ось векторной диаграммы. Активная мощность действительно работает, так что это настоящая ось.
Единицей измерения мощности является ватт (символ: W). Кажущаяся мощность часто выражается в вольт-амперы (VA), так как это продукт среднеквадратичное значение Напряжение и среднеквадратичное значение Текущий. Единицей измерения реактивной мощности является вар, что означает вольт-амперный реактивный. Поскольку реактивная мощность не передает полезную энергию нагрузке, ее иногда называют мощностью без мощности. Однако он выполняет важную функцию в электрические сети и его отсутствие было названо важным фактором Северо-восточное затемнение 2003 года.[4] Понимание взаимосвязи между этими тремя величинами лежит в основе понимания энергетики. Математические отношения между ними могут быть представлены векторами или выражены с помощью комплексных чисел, S = п + j Q (куда j это мнимая единица ).
Расчеты и уравнения
Формула для комплексной мощности (единицы: ВА) в фазор форма:
- ,
куда V обозначает напряжение в векторной форме, с амплитудой как среднеквадратичное значение, и я обозначает ток в векторной форме со среднеквадратичной амплитудой. Также по соглашению комплексно сопряженный из я используется, что обозначается (или же ), скорее, чем я сам. Это сделано потому, что в противном случае использование продукта VI для определения S приведет к количеству, которое зависит от исходного угла, выбранного для V или I, но определение S как VI * приводит к количеству, которое не зависит от исходного угла и позволяет связать S с P и Q.[5]
Другие формы комплексной мощности (единицы в вольт-амперах, ВА) получены из Z, Загрузка сопротивление (единицы в Ом, Ом).
- .
Следовательно, со ссылкой на треугольник мощности, реальная мощность (единицы измерения в ваттах, Вт) определяется как:
- .
Для чисто резистивной нагрузки реальную мощность можно упростить до:
- .
р обозначает сопротивление (единицы в Ом, Ом) нагрузки.
Реактивная мощность (единицы в вольт-амперах, реактивная мощность) рассчитывается как:
- .
Для чисто реактивной нагрузки реактивная мощность может быть упрощена до:
- ,
куда Икс обозначает реактивное сопротивление (единицы в Ом, Ом) нагрузки.
Комбинирование, комплексная мощность (единицы в вольт-амперах, ВА) вычисляется обратно как
- ,
и полная мощность (единицы в вольт-амперах, ВА) как
- .
Они схематично упрощены треугольником мощности.
Фактор силы
Отношение активной мощности к полной мощности в цепи называется фактор силы. Для двух систем, передающих одинаковое количество активной мощности, система с более низким коэффициентом мощности будет иметь более высокие циркулирующие токи из-за энергии, которая возвращается к источнику из накопителя энергии в нагрузке. Эти более высокие токи вызывают более высокие потери и снижают общую эффективность передачи. Схема с более низким коэффициентом мощности будет иметь более высокую полную мощность и более высокие потери при том же количестве активной мощности. Коэффициент мощности равен 1,0, когда напряжение и ток находятся в фаза. Он равен нулю, когда ток опережает или отстает от напряжения на 90 градусов. Когда напряжение и ток сдвинуты по фазе на 180 градусов, коэффициент мощности отрицательный, и нагрузка подает энергию в источник (примером может быть дом с солнечными батареями на крыше, которые подают энергию в электросеть, когда солнце светит). Коэффициенты мощности обычно указываются как «опережающие» или «запаздывающие», чтобы показать знак сдвига фаз тока по отношению к напряжению. Напряжение обозначается как база, с которой сравнивается угол тока, что означает, что ток рассматривается как «опережающее» или «запаздывающее» напряжение. Если форма волны чисто синусоидальная, коэффициент мощности - это косинус фазового угла () между синусоидальными сигналами тока и напряжения. В технических паспортах оборудования и паспортных табличках коэффициент мощности часто сокращается как "" по этой причине.
Пример: активная мощность 700 Вт а фазовый угол между напряжением и током составляет 45,6 °. Коэффициент мощности равен cos (45,6 °) = 0,700. Тогда кажущаяся мощность равна: 700 Вт / cos (45,6 °) = 1000 ВА. Концепция рассеивания мощности в цепи переменного тока поясняется и проиллюстрирована на примере.
Например, коэффициент мощности 0,68 означает, что только 68 процентов от общего подаваемого тока (по величине) фактически выполняет работу; остальные 32% не работают. Обычно коммунальные предприятия не взимают с потребителей плату за потери реактивной мощности, поскольку они не выполняют реальной работы для потребителя. Однако, если на источнике нагрузки потребителя наблюдается неэффективность, из-за которой коэффициент мощности падает ниже определенного уровня, коммунальные предприятия могут взимать с потребителей плату, чтобы покрыть увеличение использования топлива электростанцией и снижение мощности линии и станции.
Реактивная сила
В цепи постоянного тока мощность, протекающая к нагрузке, пропорциональна произведению тока через нагрузку и падения потенциала на нагрузке. Энергия течет в одном направлении от источника к нагрузке. В сети переменного тока напряжение и ток изменяются примерно синусоидально. Когда в цепи присутствует индуктивность или емкость, формы сигналов напряжения и тока не совпадают идеально. Поток мощности состоит из двух компонентов: один компонент течет от источника к нагрузке и может выполнять работу с нагрузкой; другая часть, известная как «реактивная мощность», возникает из-за задержки между напряжением и током, известной как фазовый угол, и не может выполнять полезную работу с нагрузкой. Его можно рассматривать как ток, который приходит не в то время (слишком поздно или слишком рано). Чтобы отличить реактивную мощность от активной, она измеряется в единицах "вольт-амперы реактивные "или var. Эти единицы можно упростить до ватт, но они оставлены как var, чтобы обозначить, что они не представляют фактической выходной мощности.
Энергия, накопленная в емкостных или индуктивных элементах сети, вызывает поток реактивной мощности. Поток реактивной мощности сильно влияет на уровни напряжения в сети. Уровни напряжения и поток реактивной мощности необходимо тщательно контролировать, чтобы энергосистема могла работать в допустимых пределах. Техника известна как реактивная компенсация используется для уменьшения кажущегося потока мощности к нагрузке за счет уменьшения реактивной мощности, подаваемой от линий электропередачи, и обеспечения ее локально. Например, чтобы компенсировать индуктивную нагрузку, рядом с самой нагрузкой устанавливают шунтирующий конденсатор. Это позволяет передавать всю реактивную мощность, необходимую нагрузке, через конденсатор и не передавать ее по линиям передачи. Такая практика позволяет экономить энергию, так как снижает количество энергии, которое необходимо произвести коммунальному предприятию для выполнения того же объема работы. Кроме того, это позволяет создавать более эффективные конструкции линий передачи с использованием проводов меньшего диаметра или меньшего количества пучков проводов и оптимизации конструкции опор передачи.
Емкостные и индуктивные нагрузки
Накопленная энергия в магнитном или электрическом поле нагрузочного устройства, такого как двигатель или конденсатор, вызывает смещение между формами колебаний тока и напряжения. Конденсатор - это устройство переменного тока, которое хранит энергию в виде электрического поля. По мере прохождения тока через конденсатор накопление заряда вызывает появление на конденсаторе противоположного напряжения. Это напряжение увеличивается до некоторого максимума, определяемого конструкцией конденсатора. В сети переменного тока напряжение на конденсаторе постоянно меняется. Конденсатор препятствует этому изменению, заставляя ток опережать напряжение по фазе. Говорят, что конденсаторы являются «источником» реактивной мощности и, таким образом, определяют ведущий коэффициент мощности.
Индукционные машины сегодня являются одними из наиболее распространенных типов нагрузки в электроэнергетической системе. Эти машины используют индукторы, или большие катушки проволоки для хранения энергии в виде магнитного поля. Когда напряжение изначально подается на катушку, индуктор сильно сопротивляется этому изменению тока и магнитного поля, что вызывает задержку по времени для достижения максимального значения тока. Это приводит к отставанию тока от напряжения по фазе. Считается, что индукторы «поглощают» реактивную мощность и, таким образом, вызывают запаздывающий коэффициент мощности. Генераторы индукционные может генерировать или поглощать реактивную мощность и обеспечивать операторам системы меры контроля над потоком реактивной мощности и, следовательно, напряжением.[6] Поскольку эти устройства оказывают противоположное влияние на фазовый угол между напряжением и током, их можно использовать для «компенсации» эффектов друг друга. Обычно это принимает форму конденсаторных батарей, используемых для противодействия отставанию коэффициента мощности, вызванному асинхронными двигателями.
Контроль реактивной мощности
Генераторы, подключенные к передаче, обычно требуются для поддержки потока реактивной мощности. Например, в системе передачи Соединенного Королевства от генераторов в соответствии с требованиями сетевого кодекса требуется обеспечивать номинальную мощность в пределах от отставания коэффициента мощности 0,85 до опережающего коэффициента мощности 0,90 на назначенных терминалах. Системный оператор будет выполнять коммутационные действия для поддержания безопасного и экономичного профиля напряжения, сохраняя при этом уравнение баланса реактивной мощности:
‘усиление системы ’Является важным источником реактивной мощности в приведенном выше уравнении баланса мощности, которая создается емкостной природой самой сети передачи. Выполнив решительные действия по переключению рано утром, до того, как спрос возрастет, выигрыш в системе может быть максимизирован на раннем этапе, помогая защитить систему в течение всего дня. Чтобы сбалансировать это уравнение, потребуется использование предаварийного реактивного генератора. Другие источники реактивной мощности, которые также будут использоваться, включают шунтирующие конденсаторы, шунтирующие реакторы, статические компенсаторы VAR и цепи управления напряжением.
Несбалансированные многофазные системы
В то время как активная мощность и реактивная мощность четко определены в любой системе, определение полной мощности для несбалансированных многофазных систем считается одной из самых спорных тем в энергетике. Первоначально кажущаяся мощность возникла просто как показатель качества. Основные очертания концепции приписываются Стэнли с Явления торможения в индукционной катушке. (1888) и Steinmetz с Теоретические основы инженерии (1915). Однако с развитием трехфазный распределения мощности, стало ясно, что определение полной мощности и коэффициента мощности нельзя применять к несимметричным многофазные системы. В 1920 году «специальный объединенный комитет AIEE и Национальной ассоциации электрического освещения» собрался, чтобы решить эту проблему. Они рассмотрели два определения.
- ,
то есть арифметическая сумма полных фазных мощностей; и
- ,
то есть величина общей трехфазной комплексной мощности.
Комитет 1920 года не нашел консенсуса, и эта тема продолжала доминировать в дискуссиях. В 1930 году сформировался другой комитет, который снова не смог решить вопрос. Стенограммы их обсуждений - самые длинные и противоречивые из всех, когда-либо опубликованных AIEE.[7] Дальнейшего разрешения этой дискуссии не было до конца 1990-х годов.
Новое определение, основанное на симметричные компоненты Теория была предложена в 1993 году Александром Эмануэлем для несимметричной линейной нагрузки, питаемой несимметричными синусоидальными напряжениями:
- ,
то есть корень из квадратов сумм линейных напряжений, умноженный на корень из квадратов сумм линейных токов. обозначает мощность прямой последовательности:
обозначает вектор напряжения прямой последовательности, а обозначает вектор тока прямой последовательности.[7]
Формулы действительных чисел
Идеальный резистор не накапливает энергии; поэтому ток и напряжение совпадают по фазе. Следовательно, нет реактивной мощности и (с использованием соглашение о пассивных знаках ). Поэтому для идеального резистора
- .
Для идеального конденсатора или катушки индуктивности нет передачи полезной мощности; так что вся мощность реактивная. Следовательно, для идеального конденсатора или индуктора:
- .
куда это реактивное сопротивление конденсатора или катушки индуктивности.
Если определяется как положительный для катушки индуктивности и отрицательный для конденсатора, тогда модуль знаки можно удалить с S и X и получить
- .
Мгновенная мощность определяется как:
- ,
куда и - изменяющиеся во времени формы сигналов напряжения и тока.
Это определение полезно, потому что оно применимо ко всем сигналам, независимо от того, являются они синусоидальными или нет. Это особенно полезно в силовой электронике, где распространены несинусоидальные сигналы.
В общем, инженеров интересует активная мощность, усредненная за период времени, будь то цикл низкочастотной линии или период переключения высокочастотного преобразователя мощности. Самый простой способ получить этот результат - взять интеграл мгновенного расчета за желаемый период:
- .
Этот метод расчета средней мощности дает активную мощность независимо от гармоническое содержание формы волны. В практических приложениях это будет выполняться в цифровой области, где расчет становится тривиальным по сравнению с использованием среднеквадратичных значений и фазы для определения активной мощности:
- .
Многочастотные системы
Поскольку среднеквадратичное значение можно рассчитать для любой формы сигнала, на его основе можно рассчитать полную мощность. Для активной мощности сначала может показаться, что необходимо рассчитать многие параметры продукта и усреднить их все. Однако более подробное рассмотрение одного из этих продуктовых терминов дает очень интересный результат.
Однако среднее по времени функции вида cos (ωt + k) равен нулю при условии, что ω не равно нулю. Следовательно, единственные термины продукта, которые имеют ненулевое среднее значение, - это те, в которых частота напряжения и тока совпадает. Другими словами, можно рассчитать активную (среднюю) мощность, просто рассматривая каждую частоту отдельно и складывая ответы. Кроме того, если предполагается, что напряжение источника питания является одночастотным (что обычно так и есть), это показывает, что гармонические токи это плохо. Они увеличивают среднеквадратичный ток (поскольку будут добавлены ненулевые члены) и, следовательно, полную мощность, но они не будут влиять на передаваемую активную мощность. Следовательно, гармонические токи уменьшают коэффициент мощности. Гармонические токи можно уменьшить с помощью фильтра, установленного на входе устройства. Обычно это будет либо просто конденсатор (в зависимости от паразитного сопротивления и индуктивности в источнике питания), либо цепь конденсатор-индуктор. Активный коррекция коэффициента мощности Схема на входе, как правило, дополнительно снижает гармонические токи и поддерживает коэффициент мощности, близкий к единице.
Смотрите также
Рекомендации
- ^ «Важность реактивной мощности для системы». 21 марта 2011 г. В архиве из оригинала на 2015-05-12. Получено 2015-04-29.
- ^ Определение активной мощности в международном электротехническом словаре В архиве 23 апреля 2015 г. Wayback Machine
- ^ IEEE 100: авторитетный словарь терминов стандартов IEEE.-7-е изд. ISBN 0-7381-2601-2, стр. 23
- ^ «Отключение 14 августа 2003 г. - последовательность событий» (PDF). FERC. 2003-09-12. Архивировано из оригинал (PDF) на 2007-10-20. Получено 2008-02-18.
- ^ Близко, Чарльз М. Анализ линейных цепей. С. 398 (раздел 8.3).
- ^ «Архивная копия». Архивировано из оригинал на 2015-10-25. Получено 2015-04-29.CS1 maint: заархивированная копия как заголовок (связь)
- ^ а б Эмануэль, Александр (июль 1993 г.). «Об определении коэффициента мощности и полной мощности в несимметричных многофазных цепях с синусоидальными напряжением и токами». Транзакции IEEE по доставке энергии. 8 (3): 841–852. Дои:10.1109/61.252612.


































![P_ text {avg} = frac {1} {n} sum_ {k = 1} ^ n V [k] I [k]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea58eff331b5263dbf27b58073ba0a5f0a0e68bf)
![begin {align}
& A cos ( omega_1t + k_1) cos ( omega_2t + k_2)
= {} & frac {A} {2} cos left [ left ( omega_1t + k_1 right) + left ( omega_2t + k_2 right) right] + frac {A} {2} cos left [ left ( omega_1t + k_1 right) - left ( omega_2t + k_2 right) right]
= {} & frac {A} {2} cos left [ left ( omega_1 + omega_2 right) t + k_1 + k_2 right] + frac {A} {2} cos left [ left ( omega_1 - omega_2 right) t + k_1 - k_2 right]
end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c773be852c41c009df2d70fc4d2e5d7ef7a36ac)