Кривая Вивианиса - Википедия - Vivianis curve

Кривая Вивиани: пересечение сферы с касательным цилиндром

Голубую часть полусферы можно возвести в квадрат.

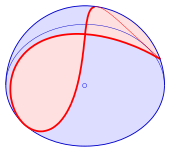
В математика, Кривая Вивиани, также известный как Окно Вивиани, это восьмерка в форме Космос изгиб назван в честь итальянского математика Винченцо Вивиани. Это пересечение сфера с цилиндр то есть касательная к сфере и проходит через центр сферы (см. диаграмму). До Вивиани эту кривую изучал Симон де ла Лубер и Жиль де Роберваль.^[1][2]

Проекция кривой Вивиани на плоскость, перпендикулярную линии, проходящей через точку пересечения, и центр сферы - это лемниската Героно.^[3]

В 1692 году Вивиани взялась за задание: вырезать из полусферы (радиус ${ displaystyle r}$) два окна, так что оставшаяся поверхность (полусферы) может быть в квадрате, т.е. квадрат с той же площадью можно построить, используя только циркуль и линейку. Его решение имеет площадь ${ displaystyle 4r ^ {2}}$ (Смотри ниже).

Уравнения

цилиндр в вертикальном положении.

Чтобы не усложнять доказательство возведения в квадрат,

то сфера имеет уравнение ${ Displaystyle ; х ^ {2} + y ^ {2} + z ^ {2} = г ^ {2} ;}$

и

то цилиндр в вертикальном положении с уравнением ${ Displaystyle ; х ^ {2} + y ^ {2} -rx = 0 ;}$.

Цилиндр имеет радиус ${ displaystyle r / 2}$ и касается сферы в точке ${ Displaystyle (г, 0,0) .}$

Свойства кривой

План этажа, фасад и боковой план

План этажа, фасад и боковой план

Устранение ${ displaystyle x}$ , ${ displaystyle y}$ , ${ displaystyle z}$ соответственно дает:

В ортогональная проекция кривой пересечения на

${ displaystyle x}$-${ displaystyle y}$-самолет круг с уравнением ${ displaystyle ; (x - { tfrac {r} {2}}) ^ {2} + y ^ {2} = ({ tfrac {r} {2}}) ^ {2} .}$

${ displaystyle x}$-${ displaystyle z}$-самолет парабола с уравнением ${ displaystyle ; x = - { tfrac {1} {r}} z ^ {2} + r ;.}$

${ displaystyle y}$-${ displaystyle z}$-самолет алгебраическая кривая с уравнением ${ displaystyle ; z ^ {4} + r ^ {2} (y ^ {2} -z ^ {2}) = 0 ;.}$

Параметрическое представление

Для параметрического представления и определения площади

Представляя сферу

${ displaystyle { begin {array} {cll} x & = & r cdot cos theta cdot cos varphi y & = & r cdot cos theta cdot sin varphi z & = & r cdot sin theta qquad qquad - { tfrac { pi} {2}} leq theta leq { tfrac { pi} {2}} , - pi leq varphi leq pi ;, end {массив}}}$

и установка ${ Displaystyle ; varphi = theta, ;}$ дает кривую

• ${ displaystyle { begin {array} {cll} x & = & r cdot cos theta cdot cos theta y & = & r cdot cos theta cdot sin theta z & = & r cdot sin theta qquad qquad - { tfrac { pi} {2}} leq theta leq { tfrac { pi} {2}} . end {array}}}$

Несложно проверить, что сферическая кривая удовлетворяет уравнению цилиндра. Но границы допускают только красную часть (см. Диаграмму) кривой Вивиани. Недостающая вторая половина (зеленая) имеет свойство ${ displaystyle ; color {зеленый} varphi = - theta ;.}$

С помощью этого параметрического представления легко доказать утверждение: площадь полусферы (содержащей кривую Вивиани) минус площадь двух окон равна ${ displaystyle 4r ^ {2}}$:

Рациональное представление Безье

Четверть кривой Вивиани, лежащая в положительном квадранте трехмерного пространства, не может быть точно представлена ​​регулярной кривой Безье любой степени.

Однако он может быть представлен точно трехмерным рациональным сегментом Безье степени 4, и существует бесконечное семейство рациональных контрольных точек Безье, порождающих этот сегмент.

Одно из возможных решений дают следующие пять контрольных точек:

${ displaystyle { boldsymbol {p0}} = { begin {bmatrix} 0 0 1 1 end {bmatrix}} { boldsymbol {p1}} = { begin {bmatrix} 0 { frac {1} {2 { sqrt {2}}}} { frac {1} { sqrt {2}}} { frac {1} { sqrt {2}}} end {bmatrix}} { boldsymbol {p2}} = { begin {bmatrix} { frac {1} {3}} { frac {1} {2}} { frac {1} { 2}} { frac {2} {3}} end {bmatrix}} { boldsymbol {p3}} = { begin {bmatrix} { frac {1} { sqrt {2}}} { frac {1} {2 { sqrt {2}}}} { frac {1} {2 { sqrt {2}}}} { frac {1} { sqrt {2 }}} end {bmatrix}} { boldsymbol {p4}} = { begin {bmatrix} 1 0 0 1 end {bmatrix}}}$

Соответствующая рациональная параметризация:

${ displaystyle left ({ begin {array} {c} { frac {2 mu ^ {2} left ( mu ^ {2} -2 left (2 + { sqrt {2}}) вправо) mu +4 { sqrt {2}} + 6 right)} { left (2 ( mu -1) mu + { sqrt {2}} + 2 right) ^ {2}} } { frac {2 ( mu -1) mu left (( mu -1) mu -3 { sqrt {2}} - 4 right)} { left (2 ( mu -1) mu + { sqrt {2}} + 2 right) ^ {2}}} - { frac {( mu -1) left ({ sqrt {2}} mu + { sqrt {2}} + 2 right)} {2 ( mu -1) mu + { sqrt {2}} + 2}} end {array}} right) ; mu in left [0,1 right]}$

Квадрат

Площадь правой верхней части окна Viviani (см. Диаграмму) можно вычислить с помощью интеграция:

${ displaystyle iint _ {S_ {сфера}} r ^ {2} cos theta , mathrm {d} theta mathrm {d} varphi = r ^ {2} int _ {0} ^ { pi / 2} int _ {0} ^ { theta} cos theta , mathrm {d} varphi mathrm {d} theta = r ^ {2} ({ frac { pi } {2}} - 1) .}$

Следовательно, общая площадь сферической поверхности, включенная в кривую Вивиани, равна ${ displaystyle 2 pi r ^ {2} -4r ^ {2}}$ и

• площадь полусферы (${ displaystyle 2 pi r ^ {2}}$) минус площадь окна Вивиани составляет ${ Displaystyle ; 4r ^ {2} ;}$, площадь квадрата с диаметром сферы, равной длине ребра.

Отношение к другим кривым

• 8-образное возвышение (см. Выше) представляет собой Лемниската Джероно.
• Кривая Вивиани - особая Кривая Клелии. Для кривой Клелии соотношение между углами равно ${ Displaystyle ; varphi = с ; theta ;.}$

Кривая Вивиани (красная) как пересечение сферы и конуса (розовая)

Вычитая 2 × уравнение цилиндра из уравнения сферы и применяя завершение квадрата приводит к уравнению

${ Displaystyle (х-г) ^ {2} + y ^ {2} = z ^ {2} ;,}$

который описывает правый круговой конус с его вершиной в${ Displaystyle ; (г, 0,0) ;}$, двойная точка кривой Вивиани. Следовательно

• Кривую Вивиани можно рассматривать не только как кривую пересечения сферы и цилиндра, но и как

а) пересечение сферы и конуса и при

б) пересечение цилиндра и конуса.

Смотрите также

• Сфера-цилиндр пересечения

Рекомендации

внешняя ссылка

• Бергер, Марсель: Геометрия. II. Перевод с французского М. Коула и С. Леви. Universitext. Springer-Verlag, Берлин, 1987.
• Бергер, Марсель: Геометрия. I. Перевод с французского М. Коула и С. Леви. Universitext. Springer-Verlag, Берлин, 1987. xiv + 428 с. ISBN  3-540-11658-3
• «Кривая Вивиани», Энциклопедия математики, EMS Press, 2001 [1994]
• Вайсштейн, Эрик В. "Кривая Вивиани". MathWorld.