Алгебраическая кривая - Algebraic curve

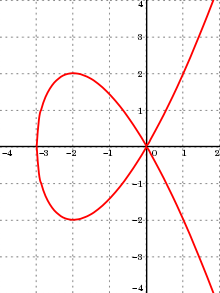
В Чирнхаузена кубическая - алгебраическая кривая степени три.

В математика, аффинная алгебраическая плоская кривая это нулевой набор из многочлен в двух переменных. А проективная алгебраическая плоская кривая нулевой набор в проективная плоскость из однородный многочлен в трех переменных. Аффинная алгебраическая плоская кривая может быть дополнена проективной алгебраической плоской кривой формулой гомогенизация его определяющий полином. Наоборот, проективная алгебраическая плоская кривая однородного уравнения $час (Икс, у, т) = 0$ можно ограничить аффинной алгебраической плоской кривой уравнения $час (Икс, у, 1) = 0$ . Каждая из этих двух операций обратный к другому; поэтому фраза алгебраическая плоская кривая часто используется без явного указания того, является ли рассматриваемый случай аффинным или проективным.

В более общем плане алгебраическая кривая является алгебраическое многообразие из измерение один. Эквивалентно, алгебраическая кривая - это алгебраическое многообразие, которое бирационально эквивалентный к алгебраической плоской кривой. Если кривая содержится в аффинное пространство или проективное пространство, можно взять проекция для такой бирациональной эквивалентности.

Эти бирациональные эквивалентности сводят большую часть изучения алгебраических кривых к изучению алгебраических плоских кривых. Однако некоторые свойства не соблюдаются при бирациональной эквивалентности и должны изучаться на неплоских кривых. Это, в частности, случай степень и гладкость. Например, существуют гладкие кривые род 0 и степени больше двух, но любая плоская проекция таких кривых имеет особые точки (см. Формула род – степень ).

Неплоскую кривую часто называют пространственная кривая или наклонная кривая.

В евклидовой геометрии

Алгебраическая кривая в Евклидова плоскость - множество точек, координаты являются решениями двумерной полиномиальное уравнение п(Икс, у) = 0. Это уравнение часто называют неявное уравнение кривой, в отличие от кривых, которые являются графиком функции, определяющей явно у как функция Икс.

Для кривой, заданной таким неявным уравнением, первая задача состоит в том, чтобы определить форму кривой и нарисовать ее. Эти проблемы не так просто решить, как в случае с графиком функции, для которого у легко вычисляется для различных значений Икс. Тот факт, что определяющее уравнение является полиномом, означает, что кривая обладает некоторыми структурными свойствами, которые могут помочь в решении этих проблем.

Каждую алгебраическую кривую можно однозначно разложить на конечное число гладких монотонных дуги (также называемый ветви) иногда соединены некоторыми точками, иногда называемыми «замечательными точками», и, возможно, конечным числом изолированных точек, называемых узлы. А гладкая монотонная дуга график гладкая функция который определяется и монотонный на открытый интервал из Икс-ось. В каждом направлении дуга либо неограничена (обычно называется бесконечная дуга) или имеет конечную точку, которая является либо особой точкой (это будет определено ниже), либо точкой с касательной, параллельной одной из координатных осей.

Например, для Чирнхаузена кубическая, есть две бесконечные дуги, имеющие начало (0,0) от конечной точки. Эта точка - единственная особая точка кривой. Есть также две дуги, имеющие эту особую точку в качестве одной конечной точки и имеющие вторую конечную точку с горизонтальной касательной. Наконец, есть две другие дуги, каждая из которых имеет одну из этих точек с горизонтальной касательной в качестве первой конечной точки и уникальную точку с вертикальной касательной в качестве второй конечной точки. Напротив, синусоида конечно, не алгебраическая кривая, имеющая бесконечное число монотонных дуг.

Чтобы нарисовать алгебраическую кривую, важно знать замечательные точки и их касательные, бесконечные ветви и их асимптоты (если есть) и способ их соединения. Также полезно учитывать точки перегиба как примечательные моменты. Когда вся эта информация нанесена на лист бумаги, форма кривой обычно видна довольно четко. Если нет, достаточно добавить несколько других точек и их касательные, чтобы получить хорошее описание кривой.

Методы вычисления примечательных точек и их касательных описаны ниже, после раздела Проективные кривые.

Плоские проективные кривые

Часто желательно рассматривать кривые в проективное пространство. Алгебраическая кривая в проективная плоскость или же плоская проективная кривая - это множество точек в проективная плоскость чей проективные координаты нули однородный многочлен в трех переменных п(Икс, у, z).

Каждая аффинная алгебраическая кривая уравнения п(Икс, у) = 0 может быть завершено в проективную кривую уравнения ${ Displaystyle ^ {ч} п (х, у, г) = 0,}$ куда

{ Displaystyle ^ {ч} п (х, у, г) = г ^ { градус (р)} р ({ tfrac {х} {z}}, { tfrac {y} {z}})}

это результат гомогенизация из п. Наоборот, если п(Икс, у, z) = 0 - однородное уравнение проективной кривой, то п(Икс, у, 1) = 0 - уравнение аффинной кривой, состоящее из точек проективной кривой, третья проективная координата которых не равна нулю. Эти две операции взаимны друг с другом, так как ${ Displaystyle ^ {ч} п (х, у, 1) = р (х, у)}$ и если п определяется ${ Displaystyle р (х, у) = п (х, у, 1)}$ , тогда ${ Displaystyle ^ {ч} п (х, у, г) = п (х, у, г),}$ , как только однородный многочлен п не делится на z.

Например, проективная кривая уравнения Икс² + у² − z² является проективным завершением единичный круг уравнения Икс² + у² − 1 = 0.

Это означает, что аффинная кривая и ее проективное пополнение являются одними и теми же кривыми, или, точнее, что аффинная кривая является частью проективной кривой, которая достаточно велика, чтобы хорошо определять «полную» кривую. Эта точка зрения обычно выражается, называя «бесконечно удаленными точками» аффинной кривой точки (в конечном числе) проективного пополнения, не принадлежащие аффинной части.

Проективные кривые часто исследуют сами по себе. Они также полезны для изучения аффинных кривых. Например, если п(Икс, у) - многочлен, определяющий аффинную кривую, помимо частных производных ${ displaystyle p '_ {x}}$ и ${ displaystyle p '_ {y}}$ , полезно учесть производная на бесконечности

{ displaystyle p '_ { infty} (x, y) = {^ {h} p' _ {z} (x, y, 1)}.}.

Например, уравнение касательной аффинной кривой уравнения п(Икс, у) = 0 в точке (а, б) является

{ displaystyle xp '_ {x} (a, b) + yp' _ {y} (a, b) + p '_ { infty} (a, b) = 0.}

Замечательные точки плоской кривой

В этом разделе мы рассмотрим плоскую алгебраическую кривую, заданную двумерным полиномом п(Икс, у) и его проективное пополнение, определяемое усреднением ${ Displaystyle P (x, y, z) = {} ^ {h} p (x, y, z)}$ из п.

Пересечение с линией

Часто бывает полезно знать точки пересечения кривой с данной линией. Пересечение с осями координат и асимптоты полезны для рисования кривой. Пересечение линией, параллельной осям, позволяет найти хотя бы точку на каждой ветви кривой. Если эффективный алгоритм поиска корней доступен, это позволяет рисовать кривую, нанося точку пересечения со всеми линиями, параллельными у-оси и проходящие через каждую пиксель на Икс-ось.

Если полином, определяющий кривую, имеет степень d, любая линия разрезает кривую не более чем на d точки. Теорема Безу утверждает, что это число точно d, если искать точки в проективной плоскости над алгебраически замкнутое поле (например, сложные числа ), и считали их множественность. Следующий метод вычислений еще раз доказывает эту теорему в этом простом случае.

Чтобы вычислить пересечение кривой, заданной полиномом п с линией уравнения топор+к+c = 0 решается уравнение прямой для Икс (или для у если а = 0). Подставляя результат в п, получаем одномерное уравнение q(у) = 0 (или q(Икс) = 0, если уравнение прямой решалось в у), каждый из корней которой является одной координатой точки пересечения. Другая координата выводится из уравнения линии. Кратность точки пересечения - это кратность соответствующего корня. Точка пересечения находится на бесконечности, если степень q ниже степени п; кратность такой бесконечно удаленной точки пересечения равна разности степеней п и q.

Касательная в точке

Касательная в точке (а, б) кривой - это линия уравнения ${ displaystyle (x-a) p '_ {x} (a, b) + (y-b) p' _ {y} (a, b) = 0}$ , как и для каждого дифференцируемая кривая определяется неявным уравнением. В случае полиномов другая формула касательной имеет более простой постоянный член и более симметрична:

{ displaystyle xp '_ {x} (a, b) + yp' _ {y} (a, b) + p '_ { infty} (a, b) = 0,}

куда ${ displaystyle p '_ { infty} (x, y) = P' _ {z} (x, y, 1)}$ - производная на бесконечности. Эквивалентность двух уравнений следует из Теорема Эйлера об однородных функциях применительно к п.

Если ${ displaystyle p '_ {x} (a, b) = p' _ {y} (a, b) = 0,}$ касательная не определена, и точка является особая точка.

Это немедленно распространяется на проективный случай: уравнение касательной к в точке проективные координаты (а:б:c) проективной кривой уравнения п(Икс, у, z) = 0 является

{ displaystyle xP '_ {x} (a, b, c) + yP' _ {y} (a, b, c) + zP '_ {z} (a, b, c) = 0,}

а особые точки кривых - это такие точки, что

{ displaystyle P '_ {x} (a, b, c) = P' _ {y} (a, b, c) = P '_ {z} (a, b, c) = 0.}

(Условие п(а, б, c) = 0 следует из этих условий по теореме Эйлера об однородных функциях.)

Асимптоты

Каждой бесконечной ветви алгебраической кривой соответствует бесконечно удаленная точка на кривой, то есть точка проективного пополнения кривой, не принадлежащая ее аффинной части. Соответствующие асимптота - касательная к кривой в этой точке. Может применяться общая формула касательной к проективной кривой, но в этом случае стоит сделать ее явной.

Позволять ${ displaystyle p = p_ {d} + cdots + p_ {0}}$ - разложение многочлена, определяющего кривую, на ее однородные части, где п_я является суммой одночленов от п степени я. Следует, что

{ displaystyle P = {^ {h} p} = p_ {d} + zp_ {d-1} + cdots + z ^ {d} p_ {0}}

и

{ displaystyle P '_ {z} (a, b, 0) = p_ {d-1} (a, b).}

Бесконечная точка кривой - это нуль п формы (а, б, 0). Эквивалентно (а, б) является нулем п_d. В основная теорема алгебры следует, что над алгебраически замкнутым полем (обычно полем комплексных чисел) п_d факторов в продукт линейных факторов. Каждый фактор определяет бесконечно удаленную точку на кривой: если bx − ай является таким фактором, то он определяет бесконечно удаленную точку (а, б, 0). По реалам, п_d делится на линейные и квадратичные множители. В несводимый квадратичные множители определяют нереальные точки на бесконечности, а действительные точки задаются линейными множителями.а, б, 0) - бесконечно удаленная точка кривой, говорят, что (а, б) является асимптотическое направление. Параметр q = п_d уравнение соответствующей асимптоты имеет вид

{ displaystyle xq '_ {x} (a, b) + yq' _ {y} (a, b) + p_ {d-1} (a, b) = 0.}

Если ${ displaystyle q '_ {x} (a, b) = q' _ {y} (a, b) = 0}$ и ${ displaystyle p_ {d-1} (a, b) neq 0,}$ асимптота - это линия на бесконечности, и в реальном случае кривая имеет ветвь, которая выглядит как парабола. В этом случае говорят, что кривая имеет параболическая ветвь. Если

{ displaystyle q '_ {x} (a, b) = q' _ {y} (a, b) = p_ {d-1} (a, b) = 0,}

кривая имеет особую точку на бесконечности и может иметь несколько асимптот. Их можно вычислить методом вычисления касательного конуса особой точки.

Особые точки

В особые точки кривой степени d определяется полиномом п(Икс,у) степени d являются решениями системы уравнений:

{ displaystyle p '_ {x} (x, y) = p' _ {y} (x, y) = p (x, y) = 0.}

В характеристика ноль, эта система эквивалентна

{ displaystyle p '_ {x} (x, y) = p' _ {y} (x, y) = p '_ { infty} (x, y) = 0,}

где, в обозначениях предыдущего раздела, ${ displaystyle p '_ { infty} (x, y) = P' _ {z} (x, y, 1).}$ Системы эквивалентны из-за Теорема Эйлера об однородных функциях. Последняя система имеет то преимущество, что ее третий многочлен степени d-1 вместо d.

Аналогично, для проективной кривой, задаваемой однородным многочленом п(Икс,у,z) степени dособые точки имеют решения системы

{ Displaystyle P '_ {x} (x, y, z) = P' _ {y} (x, y, z) = P '_ {z} (x, y, z) = 0}

в качестве однородные координаты. (В положительной характеристике уравнение ${ Displaystyle Р (х, у, г)}$ должен быть добавлен в систему.)

Отсюда следует, что число особых точек конечно, пока п(Икс,у) или же п(Икс,у,z) является без квадратов. Теорема Безу означает, что количество особых точек не превосходит (d−1)², но эта оценка не является точной, поскольку система уравнений имеет вид сверхопределенный. Если приводимые полиномы допустимы, точная оценка d(d−1) / 2, это значение достигается, когда полиномиальные множители в линейных множителях, то есть если кривая является объединением d линий. Для неприводимых кривых и многочленов количество особых точек не превосходит (d−1)(d−2) / 2 из-за формулы, выражающей род через особенности (см. Ниже). Максимума достигают кривые рода нуль, все особенности которых имеют кратность два и различные касательные (см. Ниже).

Уравнение касательных в особой точке задается ненулевой однородной частью низшей степени в Серия Тейлор полинома в особой точке. Когда вы меняете координаты, чтобы поместить особую точку в начало координат, уравнение касательных в особой точке, таким образом, является ненулевой однородной частью низшей степени полинома, а кратность особой точки является степенью этого однородного часть.

Аналитическая структура

Изучение аналитическая структура алгебраической кривой в район особой точки дает точную информацию о топологии особенностей. Фактически, вблизи особой точки действительная алгебраическая кривая представляет собой объединение конечного числа ветвей, которые пересекаются только в особой точке и выглядят либо как куспид или в виде плавной кривой.

Вблизи регулярной точки одна из координат кривой может быть выражена как аналитическая функция другой координаты. Это следствие аналитического теорема о неявной функции, откуда следует, что кривая гладкий рядом с точкой. Вблизи особой точки ситуация более сложная и включает Серия Puiseux, которые обеспечивают аналитические параметрические уравнения филиалов.

Для описания особенности стоит переведите кривая наличия особенности в начале координат. Это состоит из изменения переменной вида ${ Displaystyle X = х-а, Y = у-б,}$ куда ${ displaystyle a, b}$ - координаты особой точки. В дальнейшем предполагается, что рассматриваемая особая точка всегда находится в начале координат.

Уравнение алгебраической кривой имеет вид ${ displaystyle f (x, y) = 0,}$ куда $ж$ является многочленом от $Икс$ и $у$ . Этот многочлен можно рассматривать как многочлен от $у$ , с коэффициентами в алгебраически замкнутом поле Серия Puiseux в $Икс$ . Таким образом $ж$ могут быть учтены в факторах вида ${ Displaystyle у-Р (х),}$ куда $п$ это серия Puiseux. Все эти факторы разные, если $ж$ является неприводимый многочлен, потому что это означает, что $ж$ является без квадратов, свойство, не зависящее от поля коэффициентов.

Встречающиеся здесь серии Пюизе имеют вид

{ displaystyle P (x) = sum _ {n = n_ {0}} ^ { infty} a_ {n} x ^ {n / d},}

куда $d$ положительное целое число, и ${ displaystyle n_ {0}}$ является целым числом, которое также можно считать положительным, поскольку мы рассматриваем только те ветви кривой, которые проходят через начало координат. Без ограничения общности можно предположить, что $d$ является совмещать с наибольшим общим делителем числа $п$ такой, что ${ displaystyle a_ {n} neq 0}$ (в противном случае можно было бы выбрать меньший общий знаменатель для показателей степени).

Позволять ${ displaystyle omega _ {d}}$ быть примитивный $d$ корень единства. Если вышеуказанный ряд Пюизо встречается при факторизации ${ displaystyle f (x, y) = 0}$ , то $d$ серии

{ displaystyle P_ {i} (x) = sum _ {n = n_ {0}} ^ { infty} a_ {n} omega _ {d} ^ {i} x ^ {n / d}}

встречаются также при факторизации (следствие Теория Галуа ). Эти $d$ серии говорят сопрягать, и рассматриваются как отдельная ветвь кривой разветвление индекс $d$ .

В случае действительной кривой, то есть кривой, определяемой полиномом с действительными коэффициентами, могут иметь место три случая. Если нет ${ Displaystyle P_ {я} (х)}$ имеет действительные коэффициенты, то есть ненастоящая ветвь. Если некоторые ${ Displaystyle P_ {я} (х)}$ имеет действительные коэффициенты, то его можно выбрать как ${ Displaystyle P_ {0} (х)}$ . Если $d$ нечетно, то каждое действительное значение $Икс$ обеспечивает реальную ценность ${ Displaystyle P_ {0} (х)}$ , и у одного есть настоящая ветвь, которая выглядит правильной, хотя она является единственной, если $d > 1$ . Если $d$ четно, тогда ${ Displaystyle P_ {0} (х)}$ и ${ Displaystyle P_ {d / 2} (х)}$ имеют реальные ценности, но только для $Икс \geq 0$ . В этом случае настоящая ветка выглядит как куспид (или является куспидом, в зависимости от используемого определения куспида).

Например, у обычного куспида всего одна ветвь. Если он определяется уравнением ${ displaystyle y ^ {2} -x ^ {3} = 0,}$ то факторизация ${ Displaystyle (у-х ^ {3/2}) (у + х ^ {3/2});}$ индекс ветвления равен 2, и эти два фактора действительны и определяют каждую половину ветви. Если куспид поворачивается, уравнение становится ${ displaystyle y ^ {3} -x ^ {2} = 0,}$ и факторизация ${ displaystyle (y-x ^ {2/3}) (y-j ^ {2} x ^ {2/3}) (y- (j ^ {2}) ^ {2} x ^ {2/3}),}$ с ${ displaystyle j = (1 + { sqrt {-3}}) / 2}$ (коэффициент ${ Displaystyle (д ^ {2}) ^ {2}}$ не был упрощен до $j$ для демонстрации того, как приведенное выше определение ${ Displaystyle P_ {я} (х)}$ специализированный). Здесь индекс ветвления равен 3, и реален только один фактор; это показывает, что в первом случае эти два фактора должны рассматриваться как определяющие одну и ту же ветвь.

Неплоские алгебраические кривые

Алгебраическая кривая - это алгебраическое многообразие из измерение один. Это означает, что аффинная кривая в аффинное пространство измерения п определяется, по крайней мере, п−1 многочлен от п переменные. Чтобы определить кривую, эти многочлены должны генерировать главный идеал из Измерение Крулля 1. Это условие нелегко проверить на практике. Следовательно, может быть предпочтительным следующий способ представления неплоских кривых.

Позволять ${ displaystyle f, g_ {0}, g_ {3}, ldots, g_ {n}}$ быть п многочлены от двух переменных Икс₁ и Икс₂ такой, что ж неприводимо. Точки в аффинном пространстве размерности п такие, координаты которых удовлетворяют уравнениям и неравенствам

{ displaystyle { begin {align} & f (x_ {1}, x_ {2}) = 0 & g_ {0} (x_ {1}, x_ {2}) neq 0 x_ {3} & = { frac {g_ {3} (x_ {1}, x_ {2})} {g_ {0} (x_ {1}, x_ {2})}} & {} vdots x_ {n} & = { frac {g_ {n} (x_ {1}, x_ {2})} {g_ {0} (x_ {1}, x_ {2})}} end {align}}}

- все точки алгебраической кривой, из которых удалено конечное число точек. Эта кривая определяется системой образующих идеала многочленов час такое, что существует целое число k такой ${ displaystyle g_ {0} ^ {k} h}$ принадлежит идеалу, порожденному ${ displaystyle f, x_ {3} g_ {0} -g_ {3}, ldots, x_ {n} g_ {0} -g_ {n}}$ .Это представление бирациональная эквивалентность между кривой и плоской кривой, определяемой ж. Таким образом можно представить любую алгебраическую кривую. Однако может потребоваться линейная замена переменных, чтобы почти всегда вводить проекция от двух первых переменных. Когда необходима замена переменных, почти каждое изменение удобно, если оно определяется над бесконечным полем.

Это представление позволяет нам легко вывести любое свойство неплоской алгебраической кривой, включая ее графическое представление, из соответствующего свойства ее плоской проекции.

Для кривой, определенной ее неявными уравнениями, приведенное выше представление кривой может быть легко выведено из Основа Грёбнера для блокировать заказ такой, что блок меньших переменных равен (Икс₁, Икс₂). Полином ж - единственный полином в базе, зависящий только от Икс₁ и Икс₂. Фракции грамм_я/грамм₀ получаются выбором, для я = 3, ..., п, многочлен от базиса, линейный по Икс_я и зависит только от Икс₁, Икс₂ и Икс_я. Если этот выбор невозможен, это означает, что уравнения определяют алгебраический набор это не разнообразие, или что разнообразие не имеет размерности один, или что необходимо изменить координаты. Последний случай имеет место, когда ж существует и единственна, а при я = 3, ..., п, существуют многочлены, старший моном которых зависит только от Икс₁, Икс₂ и Икс_я.

Поля алгебраических функций

Изучение алгебраических кривых сводится к изучению несводимый алгебраические кривые: те кривые, которые нельзя записать как объединение двух меньших кривых. Вплоть до бирациональный эквивалентности неприводимые кривые над полем F находятся категорически эквивалентный к поля алгебраических функций по одной переменной более F. Такое поле алгебраических функций является расширение поля K из F который содержит элемент Икс который трансцендентный над F, и такой, что K является конечным алгебраическим расширением F(Икс) - поле рациональных функций от неопределенного Икс надF.

Например, рассмотрим поле C комплексных чисел, над которыми мы можем определить поле C(Икс) рациональных функций вC. Еслиу² = Икс³ − Икс - 1, то поле C(Икс, у) является эллиптическое функциональное поле. Элемент Икс не определяется однозначно; поле также можно рассматривать, например, как расширение C(у). Алгебраическая кривая, соответствующая полю функции, - это просто набор точек (Икс, у) в C² удовлетворение у² = Икс³ − Икс − 1.

Если поле F не является алгебраически замкнутым, точка зрения на функциональные поля немного шире, чем рассмотрение геометрического места точек, поскольку мы включаем, например, «кривые» без точек на них. Например, если базовое поле F это поле р действительных чисел, то Икс² + у² = −1 определяет поле алгебраического расширения р(Икс), но соответствующая кривая рассматривается как подмножество р² не имеет очков. Уравнение Икс² + у² = −1 действительно определяет неприводимую алгебраическую кривую над р в схема смысл ( интеграл, отделенный одномерный схемы из конечный тип над р). В этом смысле взаимно однозначное соответствие между неприводимыми алгебраическими кривыми над F (с точностью до бирациональной эквивалентности) и поля алгебраических функций от одной переменной над F держится в целом.

Две кривые могут быть бирационально эквивалентными (т. Е. Иметь изоморфный функциональные поля), не будучи изоморфными как кривые. Ситуация становится проще при работе с неособый кривые, т.е. без особенностей. Две неособые проективные кривые над полем изоморфны тогда и только тогда, когда их функциональные поля изоморфны.

Теорема Цена о функциональном поле алгебраической кривой над алгебраически замкнутым полем.

Сложные кривые и реальные поверхности

Комплексная проективная алгебраическая кривая находится в п-мерное комплексное проективное пространство CP^п. Это имеет сложное измерение п, но топологическое измерение, как реальное многообразие, 2п, и является компактный, связаны, и ориентируемый. Алгебраическая кривая над C аналогично имеет топологическую размерность два; другими словами, это поверхность.

В топологический род этой поверхности, то есть количество ручек или отверстий для бублика, равно геометрический род алгебраической кривой, которая может быть вычислена алгебраическими средствами. Короче говоря, если рассматривать плоскую проекцию неособой кривой, которая имеет степень d и только обычные особенности (особенности кратности два с различными касательными), то род равен (d − 1)(d − 2)/2 − k, куда k - количество этих особенностей.

Компактные римановы поверхности

А Риманова поверхность является связным комплексным аналитическим многообразием одного комплексного измерения, что делает его связным вещественным многообразием двух измерений. это компактный если оно компактно как топологическое пространство.

Есть тройной эквивалентность категорий между категорией гладких неприводимых проективных алгебраических кривых над C (с непостоянной обычные карты как морфизмы), категория компактных римановых поверхностей (с непостоянными голоморфные отображения как морфизмы), а противоположный категории поля алгебраических функций по одной переменной более C (с гомоморфизмами полей, фиксирующими C как морфизмы). Это означает, что, изучая эти три предмета, мы в некотором смысле изучаем одно и то же. Это позволяет использовать сложные аналитические методы в алгебраической геометрии, а алгебро-геометрические методы в комплексном анализе и теоретико-полевые методы - в обоих. Это характерно для гораздо более широкого класса задач алгебраической геометрии.

Смотрите также алгебраическая геометрия и аналитическая геометрия для более общей теории.

Особенности

Используя внутреннюю концепцию касательное пространство, точки п на алгебраической кривой C классифицируются как гладкий (синоним: неособый), иначе единственное число. Данный п−1 однородных многочленов от п+1 переменных, мы можем найти Матрица якобиана как (п−1)×(п+1) матрица частных производных. Если классифицировать этой матрицы п−1, то многочлены определяют алгебраическую кривую (в противном случае они определяют алгебраическое многообразие более высокой размерности). Если звание останется п−1, когда матрица Якоби вычисляется в точке п на кривой, то точка является гладкой или правильной точкой; в противном случае это особая точка. В частности, если кривая представляет собой плоскую проективную алгебраическую кривую, заданную одним однородным полиномиальным уравнением ж(Икс,у,z) = 0, то особые точки - это в точности точки п где ранг 1 × (п+1) матрица нулевая, то есть где

{ displaystyle { frac { partial f} { partial x}} (P) = { frac { partial f} { partial y}} (P) = { frac { partial f} { partial z}} (P) = 0.}

С ж является полиномом, это определение является чисто алгебраическим и не делает никаких предположений о природе поля F, которые, в частности, не обязательно должны быть действительными или комплексными числами. Конечно, следует помнить, что (0,0,0) не является точкой кривой и, следовательно, не является особой точкой.

Точно так же для аффинной алгебраической кривой, определенной одним полиномиальным уравнением ж(Икс,у) = 0, то особые точки - это в точности точки п кривой где ранг 1 ×п Матрица Якоби равна нулю, то есть где

{ displaystyle f (P) = { frac { partial f} { partial x}} (P) = { frac { partial f} { partial y}} (P) = 0.}

Особенности кривой не являются бирациональными инвариантами. Однако определение местоположения и классификация особенностей кривой - это один из способов вычисления род, который является бирациональным инвариантом. Чтобы это работало, мы должны рассматривать кривую проективно и требовать F быть алгебраически замкнутым, так что учитываются все особенности, принадлежащие кривой.

Классификация особенностей

Икс³ = у²

Особые точки включают несколько точек, в которых кривая пересекает себя, а также различные типы куспид, например, что показано кривой с уравнением Икс³ = у² в точке (0,0).

Кривая C имеет не более конечного числа особых точек. Если его нет, его можно назвать гладкий или же неособый. Обычно это определение понимается над алгебраически замкнутым полем и кривой C в проективное пространство (т.е. полный в смысле алгебраической геометрии). Например, плоская кривая уравнения ${ Displaystyle у-х ^ {3} = 0}$ считается особенным, поскольку имеет особую точку (куспид) на бесконечности.

В оставшейся части этого раздела рассматривается плоская кривая $C$ определяется как нулевой набор двумерного многочлена $ж (Икс, у)$ . Некоторые из результатов, но не все, можно обобщить на неплоские кривые.

Особые точки классифицируются с помощью нескольких инвариантов. Множественность $м$ определяется как максимальное целое число такое, что производные $ж$ на все заказы до $м - 1$ исчезают (также минимальный номер перекрестка между кривой и прямой на $п$ Интуитивно понятно, что особая точка имеет дельта-инвариант $δ$ если он концентрируется $δ$ обычные двойные точки на $п$ . Чтобы сделать это точным, Взрывать процесс производит так называемые бесконечно близкие точки, и суммируя $м (м -1)/2$ по бесконечно близким точкам, где м их множественность, производит $δ$ .Для неприводимой и приведенной кривой и точки $п$ мы можем определить $δ$ алгебраически как длина ${ displaystyle { widetilde {{ mathcal {O}} _ {P}}} / { mathcal {O}} _ {P}}$ куда ${ displaystyle { mathcal {O}} _ {P}}$ местное кольцо в п и ${ displaystyle { widetilde {{ mathcal {O}} _ {P}}}}$ является его интегральным замыканием.^[1]

В Число Милнора $μ$ особенности - это степень отображения $град ж (Икс, у) / | град ж (Икс, у)|$ на малой сфере радиуса ε в смысле топологической степень непрерывного отображения, куда $град ж$ - (комплексное) градиентное векторное поле ж. Это связано с δ и р посредством Формула Милнора – Юнга,

μ = 2δ - р + 1.

Здесь номер ветвления р из п - количество локально неприводимых ветвей в п. Например, р = 1 на обычном куспиде и р = 2 в обычной двойной точке. Множественность м по крайней мере р, и это п сингулярно тогда и только тогда, когда м не менее 2. Кроме того, δ не менее м(м-1)/2.

Вычисление дельта-инвариантов всех особенностей позволяет род грамм кривой, которую предстоит определить; если d это степень, тогда

{ displaystyle g = { frac {1} {2}} (d-1) (d-2) - sum _ {P} delta _ {P},}

где сумма берется по всем особым точкам п комплексной проективной плоской кривой. Это называется формула рода.

Назначьте инварианты [м, δ, р] к особенности, где м - кратность, δ - дельта-инвариант, а р это номер ветвления. Затем обыкновенный куспид - точка с инвариантами [2,1,1] и обычная двойная точка - точка с инвариантами [2,1,2], а обычная м-множественная точка - это точка с инвариантами [м, м(м−1)/2, м].

Примеры кривых

Рациональные кривые

А рациональная кривая, также называемая уникурсальной кривой, - это любая кривая, бирационально эквивалентный к линии, которую мы можем принять за проективную линию; соответственно, мы можем отождествить функциональное поле кривой с полем рациональных функций в одном неопределенном F(Икс). Если F алгебраически замкнуто, это эквивалентно кривой род нуль; однако поле всех вещественных алгебраических функций, определенных на вещественном алгебраическом многообразии Икс²+у² = −1 - поле нулевого рода, которое не является полем рациональных функций.

Конкретно, рациональная кривая, вложенная в аффинное пространство измерения п над F можно параметризовать (кроме изолированных исключительных точек) с помощью п рациональные функции одного параметра т; сводя эти рациональные функции к одному знаменателю, п+1 результирующий многочлен определяет полиномиальная параметризация из проективное завершение кривой в проективном пространстве. Примером может служитьрациональная нормальная кривая, где все эти многочлены мономы.

Любой коническая секция определяется по F с рациональная точка в F - рациональная кривая. Его можно параметризовать, нарисовав линию с уклоном т через рациональную точку и пересечение с плоской квадратичной кривой; это дает многочлен с F-рациональные коэффициенты и единица F-рациональный корень, следовательно, другой корень F-рационально (т.е. принадлежит F) также.

Икс² + ху + у² = 1

Например, рассмотрим эллипс Икс² + ху + у² = 1, где (−1, 0) - рациональная точка. Рисование линии с уклоном т из (−1,0), у = т(Икс+1), подставив его в уравнение эллипса, разложив на множители и решив для Икс, мы получаем

{ displaystyle x = { frac {1-t ^ {2}} {1 + t + t ^ {2}}}.}

Тогда уравнение для у является

{ Displaystyle у = т (х + 1) = { гидроразрыва {т (т + 2)} {1 + т + т ^ {2}}} ,,}

который определяет рациональную параметризацию эллипса и, следовательно, показывает, что эллипс является рациональной кривой. Даны все точки эллипса, кроме (−1,1), что соответствует т = ∞; поэтому вся кривая параметризована реальной проективной линией.

Такую рациональную параметризацию можно рассматривать в проективное пространство приравнивая первые проективные координаты к числителям параметризации, а последние - к общему знаменателю. Поскольку параметр определен в проективной линии, многочлены в параметре должны быть гомогенизированный. Например, проективная параметризация вышеуказанного эллипса имеет вид

{ Displaystyle X = U ^ {2} -T ^ {2}, quad Y = T , (T + 2 , U), quad Z = T ^ {2} + TU + U ^ {2} .}

Устранение Т и U между этими уравнениями мы снова получаем проективное уравнение эллипса

{ Displaystyle X ^ {2} + X , Y + Y ^ {2} = Z ^ {2},}

которое можно легко получить непосредственно путем усреднения приведенного выше уравнения.

Многие кривые в Википедии список кривых рациональны и, следовательно, имеют схожие рациональные параметризации.

Кривые рациональной плоскости

Кривые рациональной плоскости - это рациональные кривые, вложенные в ${ Displaystyle mathbb {P} ^ {2}}$ . Учитывая общие разделы ${ Displaystyle s_ {1}, s_ {2}, s_ {2} in Gamma ( mathbb {P} ^ {1}, { mathcal {O}} (d))}$ степени ${ displaystyle d}$ однородные полиномы от двух координат, ${ displaystyle x, y}$ , есть карта

${ Displaystyle s: mathbb {P} ^ {1} to mathbb {P} ^ {2}}$ данный ${ Displaystyle s ([x: y]) = [s_ {1} ([x: y]): s_ {2} ([x: y]): s_ {3} ([x: y])]}$

определение рациональной плоской кривой степени ${ displaystyle d}$ .^[2] Есть связанный пространство модулей ${ Displaystyle { mathcal {M}} = { overline { mathcal {M}}} _ {0,0} ( mathbb {P} ^ {2}, d cdot [H])}$ (куда ${ displaystyle [H]}$ класс гиперплоскости), параметризующий все такие стабильные кривые. Для определения размерности пространств модулей можно произвести подсчет размерностей: ${ displaystyle d + 1}$ параметры в ${ Displaystyle Gamma ( mathbb {P} ^ {1}, { mathcal {O}} (d))}$ давая ${ displaystyle 3d + 3}$ суммарные параметры для каждого из разделов. Тогда, поскольку они рассматриваются с точностью до проективного фактора в ${ Displaystyle mathbb {P} ^ {2}}$ есть ${ displaystyle 1}$ меньше параметра в ${ Displaystyle { mathcal {M}}}$ . Кроме того, существует трехмерная группа автоморфизмов ${ Displaystyle mathbb {P} ^ {1}}$ , следовательно ${ Displaystyle { mathcal {M}}}$ имеет размер ${ displaystyle 3d + 3-1-3 = 3d-1}$ . Это пространство модулей можно использовать для подсчета числа ${ displaystyle N_ {d}}$ степени ${ displaystyle d}$ рациональные плоские кривые пересекаются ${ displaystyle 3d-1}$ указывает, используя Теория Громова – Виттена..^[3] Он задается рекурсивным соотношением

${ displaystyle N_ {d} = sum _ {d_ {A} + d_ {B} = d} N_ {d_ {A}} N_ {d_ {B}} d_ {A} ^ {2} d_ {B} left (d_ {B} { binom {3d-4} {3d_ {A} -2}} - d_ {A} { binom {3d-4} {3d_ {A} -1}} right)}$

куда ${ Displaystyle N_ {1} = N_ {2} = 1}$ .

Эллиптические кривые

An эллиптическая кривая можно определить как любую кривую род один с рациональная точка: общая модель неособая кубическая кривая, что достаточно для моделирования любой кривой рода один. В этой модели выделенная точка обычно считается точкой перегиба на бесконечности; это означает, что кривая может быть записана в форме Тейта-Вейерштрасса, которая в своей проективной версии имеет вид

{ displaystyle y ^ {2} z + a_ {1} xyz + a_ {3} yz ^ {2} = x ^ {3} + a_ {2} x ^ {2} z + a_ {4} xz ^ { 2} + a_ {6} z ^ {3}.}

Если характеристика поля отличается от 2 и 3, то линейное изменение координат позволяет положить ${ displaystyle a_ {1} = a_ {2} = a_ {3} = 0,}$ что дает классическую форму Вейерштрасса

{ displaystyle y ^ {2} = x ^ {3} + px + q.}

Эллиптические кривые несут структуру абелева группа с выделенной точкой как тождество группового закона. В плоской кубической модели сумма трех точек в группе равна нулю тогда и только тогда, когда они коллинеарен. Для эллиптической кривой, определенной над комплексными числами, группа изоморфна аддитивной группе комплексной плоскости по модулю решетка периодов соответствующих эллиптические функции.

Пересечение двух квадратичные поверхности является, вообще говоря, неособой кривой рода один и степенью четыре и, следовательно, эллиптической кривой, если она имеет рациональную точку. В особых случаях пересечение может быть либо рациональной особой квартикой, либо разложено на кривые меньшей степени, которые не всегда различны (либо кубическая кривая и линия, либо две коники, либо коника и две прямые, либо четыре прямые) .

Кривые рода больше единицы

Кривые род больше единицы заметно отличаются как от рациональных, так и от эллиптических кривых. Такие кривые, определенные над рациональными числами, Теорема Фальтингса, могут иметь только конечное число рациональных точек, и их можно рассматривать как имеющие гиперболическая геометрия структура. Примерами являются гиперэллиптические кривые, то Кривая Клейна квартики, а Кривая Ферма Икс^п + у^п = z^п когда п больше трех. Также проективные плоские кривые в ${ Displaystyle mathbb {P} ^ {2}}$ и кривые в ${ Displaystyle mathbb {P} ^ {1} times mathbb {P} ^ {1}}$ приведу много полезных примеров.

Кривые проективной плоскости

Плоские кривые ${ Displaystyle C подмножество mathbb {P} ^ {2}}$ степени ${ displaystyle k}$ , которое может быть построено как множество исчезающих сечения общего положения ${ displaystyle s in Gamma ( mathbb {P} ^ {2}, { mathcal {O}} (k))}$ , имеет род

${ Displaystyle { гидроразрыва {(к-1) (к-2)} {2}}}$

который можно вычислить, используя Когерентные пучки когомологии. Вот краткое изложение родов кривых в зависимости от их степени.

${ displaystyle { begin {matrix} { text {deg}} & 1 & 2 & 3 & 4 & 5 & 6 & 7 { text {genus}} & 0 & 0 & 1 & 3 & 3 & 6 & 10 & 15 end {matrix}}}$

Например, кривая ${ displaystyle x ^ {4} + y ^ {4} + z ^ {4}}$ определяет кривую рода ${ displaystyle 3}$ который гладкий поскольку дифференциалы ${ displaystyle 4x ^ {3}, 4y ^ {3}, 4z ^ {3}}$ не имеют общих нулей с кривой. Не примером общего сечения является кривая ${ Displaystyle х (х ^ {2} + y ^ {2} + z ^ {2})}$ который, по Теорема Безуца, должно пересекаться не более чем ${ displaystyle 2}$ точек, является объединением двух рациональных кривых ${ Displaystyle C_ {1} чашка C_ {2}}$ пересекаются в двух точках. Примечание ${ displaystyle C_ {1}}$ задается исчезающим локусом ${ displaystyle x}$ и ${ displaystyle C_ {2}}$ задается исчезающим геометрическим местом ${ displaystyle x ^ {2} + y ^ {2} + z ^ {2}}$ . Их можно найти явно: точка лежит в обоих, если ${ displaystyle x = 0}$ . Итак, два решения - это точки ${ displaystyle [0: y: z]}$ такой, что ${ displaystyle y ^ {2} + z ^ {2} = 0}$ , которые ${ displaystyle [0: 1: -1]}$ и ${ displaystyle [0: 1: { sqrt {-1}}]}$ .

Кривые в произведении проективных линий

Изгиб ${ Displaystyle С подмножество mathbb {P} ^ {1} times mathbb {P} ^ {1}}$ заданный исчезающим локусом ${ displaystyle s in Gamma ( mathbb {P} ^ {1} times mathbb {P} ^ {1}, { mathcal {O}} (a, b))}$ , за ${ displaystyle a, b geq 2}$ , дадим кривые рода

${ displaystyle ab-a-b + 1}$

что можно проверить с помощью Когерентные пучки когомологии. Если ${ displaystyle a = 2}$ , то они определяют кривые рода ${ Displaystyle 2b-2-b + 1 = b-1}$ , следовательно, кривую любого рода можно построить как кривую в ${ Displaystyle mathbb {P} ^ {1} times mathbb {P} ^ {1}}$ . Их роды можно свести в таблице.

${ displaystyle { begin {matrix} { text {bidegree}} & (2,2) & (2,3) & (2,4) & (2,5) { text {genus}} & 1 & 2 & 3 & 4 end {matrix}}}$

и для ${ displaystyle a = 3}$ , это

${ displaystyle { begin {matrix} { text {bidegree}} & (3,2) & (3,3) & (3,4) & (3,5) { text {genus}} & 2 & 4 & 6 & 8 end {matrix}}}$

Смотрите также

Классическая алгебраическая геометрия

Современная алгебраическая геометрия

Геометрия римановых поверхностей

Примечания

^ Хартсхорн, Алгебраическая геометрия, IV Ex. 1.8.
^ Казарян, Максим Э .; Ландо, Сергей К .; Прасолов, Виктор (2018). Алгебраические кривые: к пространствам модулей. Московские лекции. Издательство Springer International. С. 213–214. ISBN 978-3-030-02942-5.
^ «Формула Концевича для рациональных плоских кривых» (PDF). В архиве (PDF) из оригинала 26 февраля 2020 г.