Коническое сечение - Conic section

Виды конических сечений:
1. Парабола
2. Круг и эллипс
3. Гипербола

Таблица коников, Циклопедия, 1728

В математика, а коническая секция (или просто конический) это изгиб полученный как пересечение поверхность из конус с самолет. Три типа конического сечения: гипербола, то парабола, а эллипс; в круг является частным случаем эллипса, хотя исторически его иногда называли четвертым типом. Древнегреческие математики изучали конические сечения, кульминацией которых стали около 200 г. до н.э. Аполлоний Пергский систематическая работа над своими свойствами.

Конические сечения в Евклидова плоскость обладают различными отличительными свойствами, многие из которых могут использоваться в качестве альтернативных определений. Одно такое свойство определяет некруглую конику^[1] быть набором тех точек, расстояние от которых до некоторой конкретной точки, называемой фокус, и некоторая конкретная линия, называемая директриса, находятся в фиксированном соотношении, называемом эксцентриситет. Тип конуса определяется величиной эксцентриситета. В аналитическая геометрия, конику можно определить как плоская алгебраическая кривая степени 2; то есть, как набор точек, координаты которых удовлетворяют квадратное уровненеие в двух переменных. Это уравнение может быть записано в матричной форме, а некоторые геометрические свойства могут быть изучены как алгебраические условия.

На евклидовой плоскости три типа конических сечений выглядят совершенно разными, но имеют много общих свойств. Расширяя евклидову плоскость, чтобы включить в нее бесконечно удаленную линию, получаем проективная плоскость, видимая разница исчезает: ветви гиперболы пересекаются в двух бесконечно удаленных точках, образуя единую замкнутую кривую; и два конца параболы встречаются, образуя замкнутую кривую, касающуюся линии на бесконечности. Дальнейшее расширение путем расширения настоящий координаты допуска сложный координат, дает возможность увидеть это объединение алгебраически.

Евклидова геометрия

Конические сечения изучались тысячи лет и дали богатый источник интересных и красивых результатов в Евклидова геометрия.

Определение

Черные границы окрашенных областей представляют собой конические участки. Не показана другая половина гиперболы, которая находится на не показанной другой половине двойного конуса.

А конический кривая, полученная как пересечение самолет, называется рубка, с поверхностью двойной конус (конус с двумя пеленки). Обычно для упрощения описания предполагается, что конус является правильным круговым конусом, но это не требуется; любой двойной конус с круглым поперечным сечением будет достаточно. Плоскости, проходящие через вершину конуса, будут пересекать конус в точке, линии или паре пересекающихся линий. Они называются вырожденные коники а некоторые авторы вообще не считают их кониками. Если не указано иное, «коника» в этой статье будет относиться к невырожденной конике.

Есть три типа конусов: эллипс, парабола, и гипербола. В круг представляет собой особый вид эллипса, хотя исторически Аполлоний считается четвертым типом. Эллипсы возникают, когда пересечение конуса и плоскости является замкнутая кривая. Окружность получается, когда секущая плоскость параллельна плоскости образующей окружности конуса; для правого конуса это означает, что секущая плоскость перпендикулярна оси. Если секущая плоскость параллельно ровно одной образующей конуса, то коника неограничена и называется парабола. В остальном случае фигура представляет собой гипербола: плоскость пересекает обе половинки конуса, образуя две отдельные неограниченные кривые.

Эксцентриситет, фокус и директриса

Эллипс (е = 1/2), парабола (е = 1) и гипербола (е = 2) с фиксированным фокусом F и директриса (е = ∞). Красный кружок (е = 0) включен для справки, у него нет направляющей в плоскости.

В качестве альтернативы можно определить коническое сечение исключительно с точки зрения геометрии плоскости: это локус всех точек п расстояние до фиксированной точки F (называется фокус ) является постоянным кратным (называемым эксцентриситет е) расстояния от п на фиксированную линию L (называется директриса).За 0 < е < 1 получаем эллипс, при е = 1 парабола, а для е > 1 гипербола.

Круг является предельным случаем и не определяется фокусом и направляющей в евклидовой плоскости. Эксцентриситет круга равен нулю, а его фокус - это центр окружности, но его направляющую можно принять только как бесконечно удаленную линию в проективной плоскости.^[2]

Эксцентриситет эллипса можно рассматривать как меру того, насколько эллипс отклоняется от круга.^[3]:844

Если угол между поверхностью конуса и его осью равен ${ displaystyle beta}$ а угол между плоскостью резания и осью равен ${ displaystyle alpha,}$ эксцентриситет^[4] ${ displaystyle { frac { cos alpha} { cos beta}}.}$

Доказательство того, что указанные выше кривые, определяемые свойство focus-directrix такие же, как и получаемые плоскостями, пересекающими конус, облегчается использованием Данделин сферы.^[5]

Конические параметры

Конические параметры в случае эллипса

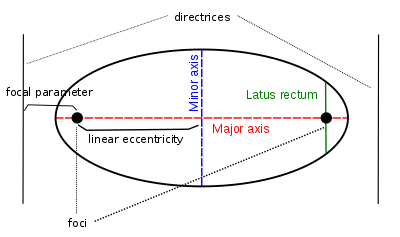
Помимо эксцентриситета (е), фокусы и директрисы, с коническим сечением связаны различные геометрические элементы и длины.

В главная ось это линия, соединяющая фокусы эллипса или гиперболы, а ее середина - это линия кривой. центр. У параболы нет центра.

В линейный эксцентриситет (c) - это расстояние между центром и фокусом.

В прямая кишка это аккорд параллельно директрисе и проходящей через фокус; его полудлина - это прямая полу-латусная мышца (ℓ).

В фокусный параметр (п) - расстояние от фокуса до соответствующей директрисы.

В большая ось хорда между двумя вершинами: самая длинная хорда эллипса, самая короткая хорда между ветвями гиперболы. Его полудлина равна большая полуось (а). Когда эллипс или гипербола находятся в стандартном положении, как в уравнениях ниже, с фокусами на Икс-ось и центр в начале координат, вершины коники имеют координаты (−а, 0) и (а, 0), с а неотрицательный.

В малая ось - наименьший диаметр эллипса, а его полудлина - малая полуось (б), то же значение б как в стандартном уравнении ниже. Аналогично для гиперболы мы также называем параметр б в стандартном уравнении - малая полуось.

Имеют место следующие соотношения:^[6]

• ${ displaystyle ell = pe}$
• ${ displaystyle c = ae}$
• ${ displaystyle p + c = { frac {a} {e}}}$

Для конусов в стандартном положении эти параметры имеют следующие значения, принимая ${ displaystyle a, b> 0}$.

коническая секция	уравнение	эксцентриситет (е)	линейный эксцентриситет (c)	полу-латусная прямая кишка (ℓ)	фокусный параметр (п)
круг	${ Displaystyle х ^ {2} + y ^ {2} = а ^ {2} ,}$	${ displaystyle 0 ,}$	${ displaystyle 0 ,}$	${ Displaystyle а ,}$	${ displaystyle infty}$
эллипс	${ displaystyle { frac {x ^ {2}} {a ^ {2}}} + { frac {y ^ {2}} {b ^ {2}}} = 1}$	${ displaystyle { sqrt {1 - { frac {b ^ {2}} {a ^ {2}}}}}}$	${ displaystyle { sqrt {a ^ {2} -b ^ {2}}}}$	${ displaystyle { frac {b ^ {2}} {a}}}$	${ displaystyle { frac {b ^ {2}} { sqrt {a ^ {2} -b ^ {2}}}}}$
парабола	${ displaystyle y ^ {2} = 4ax ,}$	${ Displaystyle 1 ,}$	Нет данных	${ displaystyle 2a ,}$	${ displaystyle 2a ,}$
гипербола	${ displaystyle { frac {x ^ {2}} {a ^ {2}}} - { frac {y ^ {2}} {b ^ {2}}} = 1}$	${ displaystyle { sqrt {1 + { frac {b ^ {2}} {a ^ {2}}}}}}$	${ displaystyle { sqrt {a ^ {2} + b ^ {2}}}}$	${ displaystyle { frac {b ^ {2}} {a}}}$	${ displaystyle { frac {b ^ {2}} { sqrt {a ^ {2} + b ^ {2}}}}}$

Стандартные формы в декартовых координатах

Стандартные формы эллипса

Стандартные формы параболы

Стандартные формы гиперболы

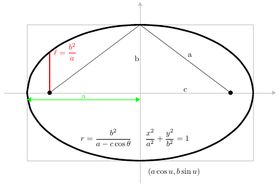
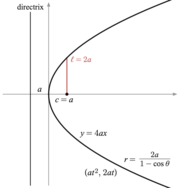
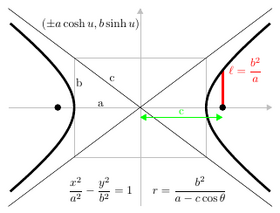
После введения Декартовы координаты, свойство focus-directrix можно использовать для получения уравнений, которым удовлетворяют точки конического сечения.^[7] Путем смены координат (вращение и перевод осей ) эти уравнения можно представить в виде стандартные формы.^[8] Стандартный вид эллипсов и гипербол имеет вид Икс- ось как главная ось и начало координат (0,0) как центр. Вершины (±а, 0) и фокусы (±c, 0). Определять б уравнениями c² = а² − б² для эллипса и c² = а² + б² для гиперболы. Для круга c = 0 так а² = б². Для параболы стандартная форма фокусируется на Икс- ось в точке (а, 0) а направляющая - прямая с уравнением Икс = −а. В стандартной форме парабола всегда проходит через начало координат.

Для прямоугольный или же равносторонний гипербола, асимптоты которого перпендикулярны, существует альтернативная стандартная форма, в которой асимптоты представляют собой оси координат и прямую Икс = у главная ось. Тогда фокусы имеют координаты (c, c) и (−c, −c).^[9]

• Круг: Икс² + у² = а²
• Эллипс: Икс²/а² + у²/б² = 1
• Парабола: у² = 4топор с а > 0
• Гипербола: Икс²/а² − у²/б² = 1
• Прямоугольная гипербола:^[10] ху = c²/2

Первые четыре из этих форм симметричны как относительно Иксось и у-оси (для окружности, эллипса и гиперболы) или около ИксТолько ось (для параболы). Однако прямоугольная гипербола симметрична относительно линий у = Икс и у = −Икс.

Эти стандартные формы можно написать параметрически в качестве,

• Круг: (а потому что θ, а грех θ),
• Эллипс: (а потому что θ, б грех θ),
• Парабола: (в², 2в),
• Гипербола: (а сек θ, б загар θ) или же (±а шиш ты, б грех ты),
• Прямоугольная гипербола: ${ displaystyle (dt, { frac {d} {t}})}$ куда ${ displaystyle d = { frac {c} { sqrt {2}}}.}$

Общая декартова форма

в Декартова система координат, то график из квадратное уровненеие в двух переменных всегда коническое сечение (хотя это может быть выродиться^[11]), и так возникают все конические сечения. Наиболее общее уравнение имеет вид^[12]

${ displaystyle Ax ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0,}$

со всеми коэффициентами действительные числа и А, Б, В не все ноль.

Матричные обозначения

Вышеупомянутое уравнение можно записать в матричных обозначениях как^[13]

${ displaystyle left ({ begin {matrix} x & y end {matrix}} right) left ({ begin {matrix} A & B / 2 B / 2 & C end {matrix}} right) left ({ begin {matrix} x y end {matrix}} right) + left ({ begin {matrix} D&E end {matrix}} right) left ({ begin {matrix} x y end {matrix}} right) + F = 0.}$

Общее уравнение также можно записать как

${ displaystyle left ({ begin {matrix} x & y & 1 end {matrix}} right) left ({ begin {matrix} A & B / 2 & D / 2 B / 2 & C & E / 2 D / 2 & E / 2 & F end {matrix}} right) left ({ begin {matrix} x y 1 end {matrix}} right) = 0.}$

Эта форма является специализацией однородной формы, используемой в более общем контексте проективной геометрии (см. ниже ).

Дискриминантный

Конические сечения, описываемые этим уравнением, можно классифицировать по величине ${ displaystyle B ^ {2} -4AC}$, называется дискриминант уравнения.^[14]Таким образом, дискриминант - 4Δ куда Δ определитель матрицы ${ displaystyle left | { begin {matrix} A & B / 2 B / 2 & C end {matrix}} right |.}$

Если коника невырожденный, тогда:^[15]

• если B² − 4AC < 0, уравнение представляет собой эллипс;
  • если А = C и B = 0, уравнение представляет собой круг, который является частным случаем эллипса;
• если B² − 4AC = 0, уравнение представляет собой парабола;
• если B² − 4AC > 0, уравнение представляет собой гипербола;
  • если А + C = 0, уравнение представляет собой прямоугольная гипербола.

В используемых здесь обозначениях А и B являются полиномиальными коэффициентами, в отличие от некоторых источников, которые обозначают большую и малую полуоси как А и B.

Инварианты

Дискриминант B² – 4AC квадратного уравнения конического сечения (или эквивалентно детерминант AC – B²/4 матрицы 2 × 2) и величина А + C (в след матрицы 2 × 2) инвариантны относительно произвольных поворотов и перемещений осей координат,^[15][16][17] как определитель Матрица 3 × 3 выше.^{[18]:стр. 60–62} Постоянный член F и сумма D²+E² инвариантны только относительно вращения.^{[18]:стр. 60–62}

Эксцентриситет с точки зрения коэффициентов

Когда коническое сечение алгебраически записывается как

${ displaystyle Ax ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0, ,}$

эксцентриситет можно записать как функцию коэффициентов квадратного уравнения.^[19] Если 4AC = B² коника является параболой и ее эксцентриситет равен 1 (при условии, что она невырожденная). В противном случае, если предположить, что уравнение представляет собой невырожденную гиперболу или эллипс, эксцентриситет определяется выражением

${ Displaystyle е = { sqrt { frac {2 { sqrt {(AC) ^ {2} + B ^ {2}}}} { eta (A + C) + { sqrt {(AC) ^ {2} + B ^ {2}}}}}},}$

куда η = 1 если определитель Матрица 3 × 3 выше отрицательный и η = −1 если этот определитель положительный.

Это также может быть показано^{[18]:п. 89} что эксцентриситет является положительным решением уравнения

${ displaystyle Delta e ^ {4} + [(A + C) ^ {2} -4 Delta] e ^ {2} - [(A + C) ^ {2} -4 Delta] = 0, }$

где снова ${ displaystyle Delta = AC - { frac {B ^ {2}} {4}}.}$ У этого есть ровно одно положительное решение - эксцентриситет - в случае параболы или эллипса, тогда как в случае гиперболы у него есть два положительных решения, одно из которых - эксцентриситет.

Преобразование в каноническую форму

В случае эллипса или гиперболы уравнение

${ displaystyle Ax ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0 ,}$

можно преобразовать в каноническую форму в преобразованных переменных ${ displaystyle x ', y'}$ в качестве^[20]

${ displaystyle { frac {x '^ {2}} {- S / ( lambda _ {1} ^ {2} lambda _ {2})}} + { frac {y' ^ {2}} {-S / ( lambda _ {1} lambda _ {2} ^ {2})}} = 1,}$

или эквивалентно

${ displaystyle { frac {x '^ {2}} {- S / ( lambda _ {1} Delta)}} + { frac {y' ^ {2}} {- S / ( lambda _ {2} Delta)}} = 1,}$

куда ${ displaystyle lambda _ {1}}$ и ${ displaystyle lambda _ {2}}$ являются собственные значения матрицы ${ displaystyle left ({ begin {matrix} A & B / 2 B / 2 & C end {matrix}} right)}$ - то есть решения уравнения

${ displaystyle lambda ^ {2} - (A + C) lambda + (AC- (B / 2) ^ {2}) = 0}$

- и ${ displaystyle S}$ является определителем Матрица 3 × 3 выше, и ${ displaystyle Delta = lambda _ {1} lambda _ {2}}$ снова является определителем матрицы 2 × 2. В случае эллипса квадраты двух полуосей задаются знаменателями в канонической форме.

Полярные координаты

Развитие конического сечения как эксцентриситета е увеличивается

В полярные координаты, коническое сечение с одним фокусом в начале координат и, если есть, другим с отрицательным значением (для эллипса) или положительным значением (для гиперболы) на Иксось, задается уравнением

${ displaystyle r = { frac {l} {1 + e cos theta}},}$

куда е это эксцентричность и л представляет собой прямую половину прямой кишки.

Как и выше, для е = 0, график - круг, при 0 < е < 1график представляет собой эллипс, для е = 1 парабола, а для е > 1 гипербола.

Полярная форма уравнения коники часто используется в динамика; например, определение орбит объектов, вращающихся вокруг Солнца.^[21]

Характеристики

Как две (разные) точки определяют линию, пять точек определяют конус. Формально, учитывая любые пять точек на плоскости в общее линейное положение, то есть нет три коллинеарен, через них проходит единственная коника, которая будет невырожденной; это верно как для евклидовой плоскости, так и для ее продолжения, реальной проективной плоскости. В самом деле, для любых пяти точек через них проходит коника, но если три точки лежат на одной прямой, то коника будет вырожденной (приводимой, поскольку она содержит прямую) и может не быть единственной; видеть дальнейшее обсуждение.

Четыре точки на плоскости в общем линейном положении определяют уникальную конику, проходящую через первые три точки и имеющую четвертую точку в качестве своего центра. Таким образом, знание центра эквивалентно знанию двух точек на конике с целью определения кривой.^[22]

Кроме того, конус определяется любой комбинацией k точки в общем положении, через которые он проходит, и 5 - k касательные к нему, при 0≤k≤5.^[23]

Любая точка на плоскости находится либо на нуле, либо на единице, либо на двух. касательные линии коники. Точка только на одной касательной находится на конике. Точка без касательной называется внутренняя точка (или же внутренняя точка) коники, а точка на двух касательных - внешняя точка (или же внешняя точка).

Все конические секции имеют общий свойство отражения Это можно сформулировать так: Все зеркала в форме невырожденного конического сечения отражают свет, идущий от одного фокуса или идущий к нему, к другому фокусу или от него. В случае параболы второй фокус нужно рассматривать как бесконечно удаленный, чтобы световые лучи, идущие к второму фокусу или исходящие от него, были параллельны.^[24][25]

Теорема Паскаля касается коллинеарности трех точек, построенных из шести точек на любой невырожденной конике. Теорема верна и для вырожденных коник, состоящих из двух прямых, но в этом случае она известна как Теорема Паппа.

Невырожденные конические сечения всегда "гладкий ". Это важно для многих приложений, таких как аэродинамика, где требуется гладкая поверхность для обеспечения ламинарный поток и предотвратить турбулентность.

История

Менехм и ранние произведения

Считается, что первое определение конического сечения было дано Менахм (умер в 320 г. до н.э.) в рамках своего решения делосской проблемы (Дублирование куба ).^[26][27] Его работы не сохранились, даже названия, которые он использовал для этих кривых, и известны только из вторичных источников.^[28] Определение, которое использовалось в то время, отличается от того, что обычно используется сегодня. Конусы были построены путем вращения прямоугольного треугольника вокруг одного из его катетов, так что гипотенуза образует поверхность конуса (такая линия называется образующая ). Три типа конусов были определены по углам их вершин (измеренным как удвоенный угол, образованный гипотенузой и катетом, вращающимся вокруг прямоугольного треугольника). Затем определялось коническое сечение путем пересечения одного из этих конусов плоскостью, перпендикулярной образующей. Тип конуса определяется типом конуса, то есть углом, образованным в вершине конуса: если угол острый, то коника является эллипсом; если угол прямой, то коника - парабола; а если угол тупой, то коника - это гипербола (но только одна ветвь кривой).^[29]

Евклид (около 300 г. до н. э.), как говорят, написал четыре книги о кониках, но и они были утеряны.^[30] Архимед (умер около 212 г. до н.э.), как известно, изучал коники, определяя площадь, ограниченную параболой и хордой в Квадратура параболы. Его основной интерес был с точки зрения измерения площадей и объемов фигур, связанных с кониками, и часть этой работы сохранилась в его книге о телах вращения коников. О коноидах и сфероидах.^[31]

Аполлоний Пергский

Схема из Аполлония Коники, в арабском переводе IX века

Наибольший прогресс в изучении коник древними греками был достигнут благодаря Аполлоний Пергский (умер около 190 г. до н. э.), восьмитомник которого Конические сечения или же Коники обобщены и значительно расширены существующие знания.^[32] Изучение Аполлонием свойств этих кривых позволило показать, что любая плоскость, пересекающая фиксированный двойной конус (две вершины), независимо от ее угла, будет давать конус в соответствии с более ранним определением, что привело к определению, которое обычно используется сегодня. Таким образом также можно получить круги, которые нельзя построить предыдущим методом. Это может объяснить, почему Аполлоний считал окружности четвертым типом конического сечения, но это различие больше не проводится. Аполлоний использовал имена эллипс, парабола и гипербола для этих кривых, заимствуя терминологию из более ранних работ Пифагора о площадях.^[33]

Папп Александрийский (умер ок. 350 г. н. э.) приписывают разъяснение важности концепции фокусировки конуса и детальное описание связанной концепции конуса. директриса, в том числе случай параболы (которого нет в известных трудах Аполлония).^[34]

Аль-Кухи

Инструмент для рисования конических сечений был впервые описан в 1000 году н.э. исламским математиком. Аль-Кухи.^[35]:30[36]

Омар Хайям

Работа Аполлония была переведена на арабский язык, и большая часть его работ сохранилась только в арабской версии. Персы нашли приложения теории, в первую очередь персидские^[37] математик и поэт Омар Хайям, нашедший геометрический метод решения кубические уравнения с использованием конических участков.^[38][39]

Европа

Иоганн Кеплер расширил теорию коник через "принцип преемственности ", предшественник концепции пределов. Кеплер впервые использовал термин фокусы в 1604 г.^[40]

Жирар Дезарг и Блез Паскаль разработал теорию коников, используя раннюю форму проективная геометрия и это помогло придать импульс изучению этой новой области. В частности, Паскаль открыл теорему, известную как гексаграмма мистикум из которого можно вывести многие другие свойства коник.

Рене Декарт и Пьер Ферма оба применили свои недавно открытые аналитическая геометрия к изучению коников. В результате геометрические проблемы коник были сведены к задачам алгебры. Однако это было Джон Уоллис в его трактате 1655 г. Tractatus de sectionibus conicis кто первым определил конические сечения как примеры уравнений второй степени.^[41] Написано ранее, но опубликовано позже, Ян де Витт с Elementa Curvarum Linearum начинается с Кеплера кинематический построение коник, а затем построение алгебраических уравнений. Эта работа, в которой используется методология Ферма и нотация Декарта, была названа первым учебником по этому предмету.^[42] Де Витт изобрел термин директриса.^[42]

Приложения

В параболоид форма Археоциатиды производит конические участки на забоях горных пород

Конические сечения важны в астрономия: the орбиты двух массивных объектов, которые взаимодействуют согласно Закон всемирного тяготения Ньютона являются коническими сечениями, если их общие центр массы считается в состоянии покоя. Если они связаны вместе, они оба начертят эллипсы; если они расходятся, они оба будут следовать параболам или гиперболам. Видеть проблема двух тел.

Отражающие свойства конических секций используются в конструкции прожекторов, радиотелескопов и некоторых оптических телескопов.^[43] В прожекторах в качестве отражателя используется параболическое зеркало с лампочкой в ​​фокусе; и аналогичная конструкция используется для параболический микрофон. 4,2 метра Оптический телескоп Herschel на Ла-Пальма, на Канарских островах, использует первичное параболическое зеркало, чтобы отражать свет к вторичному гиперболическому зеркалу, которое снова отражает его в фокус за первым зеркалом.

В реальной проективной плоскости

Конические сечения имеют некоторые очень похожие свойства в евклидовой плоскости, и причины этого становятся более ясными, когда коники рассматриваются с точки зрения более крупной геометрии. Евклидова плоскость может быть вложена в реальная проективная плоскость и коники можно рассматривать как объекты в этой проективной геометрии. Один из способов сделать это - ввести однородные координаты и определим конику как набор точек, координаты которых удовлетворяют неприводимому квадратному уравнению с тремя переменными (или, что то же самое, нули неприводимого квадратичная форма ). Более технически, множество точек, которые являются нулями квадратичной формы (при любом количестве переменных), называется квадрика, а неприводимые квадрики в двумерном проективном пространстве (т. е. с тремя переменными) традиционно называют кониками.

Евклидова плоскость р² вкладывается в действительную проективную плоскость путем присоединения линия на бесконечности (и соответствующий указывает на бесконечность ) так, чтобы все прямые параллельного класса пересекались на этой прямой. С другой стороны, начиная с реальной проективной плоскости, евклидова плоскость получается путем выделения некоторой прямой как линии на бесконечности и удаления ее и всех ее точек.

Пересечение в бесконечности

В проективное пространство над любым телом, но, в частности, над действительными или комплексными числами, все невырожденные коники эквивалентны, и поэтому в проективной геометрии просто говорят о «конике», не указывая тип. То есть существует проективное преобразование, которое отображает любую невырожденную конику на любую другую невырожденную конику.^[44]

Три типа конических сечений снова появятся в аффинной плоскости, полученной путем выбора прямой проекционного пространства в качестве линии на бесконечности. Затем эти три типа определяются по тому, как эта бесконечно удаленная линия пересекает конику в проективном пространстве. В соответствующем аффинном пространстве получается эллипс, если коника не пересекает прямую на бесконечности, парабола, если коника пересекает прямую на бесконечности за один двойная точка соответствующей оси, и гипербола, если коника пересекает бесконечно удаленную прямую в двух точках, соответствующих асимптотам.^[45]

Однородные координаты

В однородные координаты коническое сечение можно представить как:

${ displaystyle Ax ^ {2} + Bxy + Cy ^ {2} + Dxz + Eyz + Fz ^ {2} = 0.}$

Или в матрица обозначение

${ displaystyle left ({ begin {matrix} x & y & z end {matrix}} right) left ({ begin {matrix} A & B / 2 & D / 2 B / 2 & C & E / 2 D / 2 & E / 2 & F end {matrix}} right) left ({ begin {matrix} x y z end {matrix}} right) = 0.}$

Матрица 3 × 3 выше называется матрица конического сечения.

Некоторые авторы предпочитают записывать общее однородное уравнение в виде

${ displaystyle Ax ^ {2} + 2Bxy + Cy ^ {2} + 2Dxz + 2Eyz + Fz ^ {2} = 0,}$

(или его разновидность), так что матрица конического сечения имеет более простой вид:

${ Displaystyle M = left ({ begin {matrix} A & B & D B & C & E D & E & F end {matrix}} right),}$

но это обозначение не используется в данной статье.^[46]

Если определитель матрицы конического сечения равен нулю, коническое сечение равно выродиться.

Поскольку умножение всех шести коэффициентов на один и тот же ненулевой скаляр дает уравнение с тем же набором нулей, можно рассматривать коники, представленные (А, B, C, D, E, F) как точки в пятимерном проективное пространство ${ displaystyle mathbf {P} ^ {5}.}$

Проективное определение круга

Метрический концепции евклидовой геометрии (понятия, связанные с измерением длины и углов) не могут быть немедленно распространены на реальную проективную плоскость.^[47] Они должны быть переопределены (и обобщены) в этой новой геометрии. Это можно сделать для произвольных проективные плоскости, но чтобы получить реальную проективную плоскость как расширенную евклидову плоскость, необходимо сделать некоторые конкретные выборы.^[48]

Зафиксируем произвольную прямую на проективной плоскости, которую мы будем называть абсолютная линия. Выберите две различные точки на абсолютной прямой и назовите их абсолютные баллы. Со ссылкой на эти варианты можно определить несколько метрических концепций. Например, учитывая строку, содержащую точки А и B, то середина линейного сегмента AB определяется как точка C какой проективное гармоническое сопряжение точки пересечения AB и абсолютная линия относительно А и B.

Коника на проективной плоскости, содержащая две абсолютные точки, называется коникой. круг. Поскольку пять точек определяют конику, окружность (которая может быть вырожденной) определяется тремя точками. Чтобы получить расширенную евклидову плоскость, абсолютная прямая выбирается как бесконечно удаленная от евклидовой плоскости, а абсолютные точки - это две особые точки на этой прямой, называемые прямой. круговые точки на бесконечности. Линии, содержащие две точки с действительными координатами, не проходят через круговые точки на бесконечности, поэтому на евклидовой плоскости круг в соответствии с этим определением определяется тремя точками, которые не являются коллинеарен.^[49]:72

Было упомянуто, что окружности в евклидовой плоскости не могут быть определены свойством фокус-директрисы. Однако, если рассматривать бесконечно удаленную прямую как направляющую, то, принимая эксцентриситет равным е = 0 круг будет иметь свойство focus-directrix, но он все еще не определяется этим свойством.^[50] В этой ситуации нужно быть осторожным, чтобы правильно использовать определение эксцентриситета как отношение расстояния от точки на окружности до фокуса (длина радиуса) к расстоянию от этой точки до направляющей (это расстояние бесконечно). что дает нулевое предельное значение.

Проективное коническое определение Штейнера

Определение генерации Штейнера конического сечения

А синтетический (безкоординатный) подход к определению конических сечений на проективной плоскости был дан Якоб Штайнер в 1867 г.

• Учитывая два карандаша ${ Displaystyle B (U), B (V)}$ линий в двух точках ${ displaystyle U, V}$ (все строки, содержащие ${ displaystyle U}$ и ${ displaystyle V}$ соотв.) и проективный но нет перспектива отображение ${ displaystyle pi}$ из ${ Displaystyle B (U)}$ на ${ Displaystyle B (V)}$. Тогда точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение.^{[51][52][53][54]}

А перспектива отображение ${ displaystyle pi}$ карандаша ${ Displaystyle B (U)}$ на карандаш ${ Displaystyle B (V)}$ это биекция (Соответствие 1-1) такое, что соответствующие прямые пересекаются на фиксированной прямой ${ displaystyle a}$, который называется ось перспективы ${ displaystyle pi}$.

А проективный отображение - это конечная последовательность перспективных отображений.

Как проективное отображение на проективной плоскости над полем (паппийский самолет ) однозначно определяется заданием изображений трех линий,^[55] для генерации Штейнера конического сечения, кроме двух точек ${ displaystyle U, V}$ необходимо указать только изображения трех строк. Эти 5 элементов (2 точки, 3 линии) однозначно определяют коническое сечение.

Линия коники

Посредством Принцип двойственности в проективной плоскости двойственная точка каждой точки является прямой, а двойственная точка множества точек (набор точек, удовлетворяющих некоторому условию) называется конверт линий. Используя определение коники Штейнера (теперь это геометрическое место точек будем называть точечный конический) как пересечение соответствующих лучей двух связанных пучков, легко дуализировать и получить соответствующую огибающую, состоящую из соединений соответствующих точек двух связанных диапазонов (точек на прямой) на разных основаниях (прямых, на которых находятся точки) . Такой конверт называется линия коническая (или же двойная коническая).

В реальной проективной плоскости точечная коника обладает тем свойством, что каждая прямая пересекает ее в двух точках (которые могут совпадать или могут быть комплексными), и любой набор точек с этим свойством является точечной коникой. Отсюда вдвойне следует, что у прямой коники есть две прямые, проходящие через каждую точку, и любая огибающая прямых с этим свойством является прямой конической. В каждой точке конической точки имеется единственная касательная линия, и вдвойне на каждой прямой конической прямой есть единственная точка, называемая точка касания. Важная теорема утверждает, что касательные линии точечной коники образуют прямую конику, а точки соприкосновения прямой коники образуют коническую точку.^[56]:48–49

Определение фон Штаудта

Карл Георг Кристиан фон Штаудт определил конику как набор точек, заданный всеми абсолютными точками полярность который имеет абсолютные точки. Фон Штаудт ввел это определение в Geometrie der Lage (1847) как часть его попытки удалить все метрические концепции из проективной геометрии.

А полярность, π, проективной плоскости, п, является инволютивным (т. е. второго порядка) биекция между точками и линиями п что сохраняет отношение инцидентности. Таким образом, полярность связывает точку Q с линией q и, следуя Gergonne, q называется полярный из Q и Q в столб из q.^[57] An абсолютная точка (линия) полярности - это тот, который падает со своей полярностью (полюсом).^[58]

Коника фон Штаудта в вещественной проективной плоскости эквивалентна Конус Штейнера.^[59]

Конструкции

Невозможно построить непрерывную дугу коники с помощью линейки и циркуля. Однако существует несколько построений линейки и циркуля для любого количества отдельных точек на дуге.

Один из них основан на обратной теореме Паскаля, а именно, если точки пересечения противоположных сторон шестиугольника лежат на одной прямой, то шесть вершин лежат на конике. В частности, учитывая пять баллов, А, B, C, D, E и линия, проходящая через E, сказать НАПРИМЕР, точка F который лежит на этой прямой и находится на конике, определяемой пятью точками. Позволять AB встретить DE в L, до н.э встретить НАПРИМЕР в M и разреши CD встретить LM в N. потом AN встречает НАПРИМЕР в нужной точке F.^[60]:52–53 Изменяя линию через E, можно построить сколько угодно дополнительных точек на конике.

Метод параллелограмма для построения эллипса

Другой метод, основанный на конструкции Штейнера и полезный в инженерных приложениях, - это метод метод параллелограмма, где коника строится по точкам путем соединения некоторых равноотстоящих точек на горизонтальной и вертикальной линиях.^[61] В частности, чтобы построить эллипс по уравнению Икс²/а² + у²/б² = 1, сначала постройте прямоугольник ABCD с вершинами А(а, 0), B(а, 2б), C(−а, 2б) и D(−а, 0). Разделите сторону до н.э в п равные отрезки и используйте параллельную проекцию относительно диагонали AC, чтобы сформировать равные отрезки по бокам AB (длины этих отрезков будут б/а раз больше длины сегментов на до н.э). На стороне до н.э пометьте левые конечные точки сегментов А₁ к А_п начинается с B и иду к C. На стороне AB обозначить верхние конечные точки D₁ к D_п начинается с А и иду к B. Точки пересечения, AA_я ∩ DD_я за 1 ≤ я ≤ п будут точками эллипса между А и п(0, б). Маркировка связывает линии карандаша через А линиями карандаша через D проективно, но не перспективно. Искомая коника получается этой конструкцией, поскольку три точки А, D и п и две касательные (вертикальные линии на А и D) однозначно определяют конику. Если другой диаметр (и сопряженный к нему диаметр) используется вместо большой и малой осей эллипса, в конструкции используется параллелограмм, который не является прямоугольником, давая имя методу. Объединение линий карандашей может быть расширено, чтобы получить другие точки на эллипсе. Конструкции для гипербол^[62] и параболы^[63] похожи.

Еще один общий метод использует свойство полярности для построения касательной огибающей коники (прямой коники).^[64]

В комплексной проективной плоскости

В комплексной плоскости C², эллипсы и гиперболы неотличимы: можно рассматривать гиперболу как эллипс с мнимой длиной оси. Например, эллипс ${ displaystyle x ^ {2} + y ^ {2} = 1}$ становится гиперболой при замене ${ displaystyle y = iw,}$ геометрически сложное вращение, дающее ${ displaystyle x ^ {2} -w ^ {2} = 1}$. Таким образом, существует двухсторонняя классификация: эллипс / гипербола и парабола. Продолжение кривых на комплексную проективную плоскость соответствует пересечению линия на бесконечности либо в 2 различных точках (соответствующих двум асимптотам), либо в 1 двойной точке (соответствующей оси параболы); таким образом, реальная гипербола является более убедительным реальным изображением для сложного эллипса / гиперболы, поскольку она также имеет 2 (реальных) пересечения с линией на бесконечности.

Дальнейшее объединение происходит в комплексная проективная плоскость CP²: невырожденные коники нельзя отличить друг от друга, так как любая может быть переведена в любую другую проективное линейное преобразование.

Можно доказать, что в CP², два конических участка имеют четыре общие точки (если учесть множественность ), поэтому имеется от 1 до 4 пересечение точки. Возможны следующие варианты пересечения: четыре различные точки, две особые точки и одна двойная точка, две двойные точки, одна особая точка и одна с кратностью 3, одна точка с кратностью 4. Если любая точка пересечения имеет кратность> 1, две кривые называются быть касательная. Если имеется точка пересечения кратности не менее 3, две кривые называются ласкать. Если имеется только одна точка пересечения, кратность которой равна 4, две кривые называются сверхскоростной.^[65]

Кроме того, каждый прямая линия дважды пересекает каждое коническое сечение. Если точка пересечения двойная, линия является касательная линия.Каждое коническое сечение, пересекающееся с линией на бесконечности, имеет две бесконечно удаленные точки. Если эти точки действительны, кривая представляет собой гипербола; если они мнимые конъюгаты, это эллипс; если есть только одна двойная точка, это парабола. Если бесконечно удаленные точки являются циклические точки (1, я, 0) и (1, –я, 0), коническое сечение является круг. Если коэффициенты конического сечения действительны, бесконечно удаленные точки либо действительны, либо комплексно сопряженный.

Вырожденные случаи

Что следует рассматривать как вырожденный случай коники зависит от используемого определения и геометрических параметров конического сечения. Некоторые авторы определяют конику как двумерную невырожденную квадрику. В этой терминологии нет вырожденных коник (только вырожденные квадрики), но мы будем использовать более традиционную терминологию и избегать этого определения.

В евклидовой плоскости, используя геометрическое определение, возникает вырожденный случай, когда секущая плоскость проходит через вершина конуса. Вырожденная коника есть либо: точка, когда плоскость пересекает конус только на вершине; а прямая линия, когда плоскость касается конуса (содержит ровно одну образующую конуса); или пара пересекающихся прямых (две образующие конуса).^[66] Они соответствуют соответственно предельным формам эллипса, параболы и гиперболы.

Если коника в евклидовой плоскости определяется нулями квадратного уравнения (то есть как квадрика), то вырожденными кониками являются: пустой набор, точка или пара прямых, которые могут быть параллельны, пересекаться в точке или совпадать. Случай пустого множества может соответствовать либо паре комплексно сопряженный параллельные линии, например, с уравнением ${ displaystyle x ^ {2} + 1 = 0,}$ или к воображаемый эллипс, например, с уравнением ${ displaystyle x ^ {2} + y ^ {2} + 1 = 0.}$ Мнимый эллипс не удовлетворяет общему определению вырождение, и поэтому обычно не считается вырожденным.^[67] Случай двух линий возникает, когда квадратичное выражение делится на два линейных множителя, нули каждого из которых дают линию. В случае, если множители совпадают, соответствующие линии совпадают, и мы называем линию a. двойной линия (линия с множественность 2), и это предыдущий случай касательной секущей плоскости.

В реальной проективной плоскости, поскольку параллельные прямые пересекаются в точке на бесконечности, случай параллельной прямой евклидовой плоскости можно рассматривать как пересекающиеся линии. Однако, поскольку точка пересечения является вершиной конуса, сам конус вырождается в цилиндр, т.е. с бесконечно удаленной вершиной. Остальные разделы в этом случае называются цилиндрические секции.^[68] Невырожденные цилиндрические участки представляют собой эллипсы (или окружности).

Если смотреть с точки зрения комплексной проективной плоскости, вырожденные случаи действительной квадрики (т. Е. Квадратное уравнение имеет действительные коэффициенты) можно рассматривать как пару прямых, возможно, совпадающих. Пустым набором может быть бесконечно удаленная линия, рассматриваемая как двойная линия, (реальная) точка - это пересечение двух комплексно сопряженные линии и другие случаи, как упоминалось ранее.

Чтобы отличать вырожденные случаи от невырожденных случаев (включая пустое множество с последним) с помощью матричных обозначений, пусть β - определитель матрицы 3 × 3 конического сечения, т. е. β = (AC − B²/4)F + КРОВАТЬ − CD² − AE²/4; и разреши α = B² − 4AC быть дискриминантом. Тогда коническое сечение невырождено тогда и только тогда, когда β ≠ 0. Если β = 0 у нас есть момент, когда α < 0, две параллельные прямые (возможно, совпадающие), когда α = 0, или две пересекающиеся линии, когда α > 0.^[69]

Карандаш коников

(Невырожденная) коника полностью определяется формулой пять баллов в общем положении (нет трех коллинеарен ) на плоскости, а система коник, которые проходят через фиксированный набор из четырех точек (опять же в плоскости, а не трех коллинеарных), называется карандаш коников.^[70]:64 Четыре общие точки называются базовые точки карандаша. Через любую точку, кроме базовой, проходит единственная коника карандаша. Эта концепция обобщает карандаш кругов.^[71]:127

Пересечение двух коник

Решения системы двух уравнений второй степени с двумя переменными можно рассматривать как координаты точек пересечения двух общих конических сечений. В частности, две коники могут не иметь ни одной, а могут иметь две или четыре, возможно, совпадающих точек пересечения. при поиске этих решений используется однородная матричное представление конических сечений, т.е. 3x3 симметричная матрица которое зависит от шести параметров.

Процедура определения точек пересечения состоит из следующих шагов, где коники представлены матрицами:^[72]

• учитывая две коники ${ displaystyle C_ {1}}$ и ${ displaystyle C_ {2}}$рассмотрим пучок коник, заданный их линейной комбинацией ${ displaystyle lambda C_ {1} + mu C_ {2}.}$
• определить однородные параметры ${ Displaystyle ( лямбда, му)}$ которые соответствуют вырожденной конике пучка. Это можно сделать, поставив условие, что ${ Displaystyle Det ( лямбда C_ {1} + mu C_ {2}) = 0}$ и решение для ${ displaystyle lambda}$ и ${ displaystyle mu}$. Оказывается, это решения уравнения третьей степени.
• учитывая вырожденную конику ${ displaystyle C_ {0}}$, определите две, возможно совпадающие, линии, составляющие его.
• пересечь каждую идентифицированную линию с одной из двух исходных коник; этот шаг можно эффективно выполнить, используя двойственное коническое представление ${ displaystyle C_ {0}}$
• точки пересечения будут представлять решения исходной системы уравнений.

Обобщения

Коники могут быть определены поверх других полей (т. Е. В других паппиевы геометрии ). Однако следует проявлять некоторую осторожность, когда поле характеристика 2, так как некоторые формулы использовать нельзя. Например, используемые матричные представления над требуется деление на 2.

Обобщением невырожденной коники на проективной плоскости является овал. Овал - это набор точек, который обладает следующими свойствами, которые поддерживаются кониками: 1) любая прямая пересекает овал ни в одной, одной или двух точках, 2) в любой точке овала существует единственная касательная линия.

Обобщение свойств фокуса коник на случай, когда имеется более двух фокусов, дает наборы, называемые обобщенные коники.

В других областях математики

Классификация на эллиптические, параболические и гиперболические широко распространена в математике и часто делит поле на четко определенные подполя. Классификация в основном возникает из-за наличия квадратичной формы (в двух переменных это соответствует ассоциированной дискриминант ), но также может соответствовать эксцентриситету.

Классификация квадратичных форм:

Квадратичные формы

Квадратичные формы над вещественными числами классифицируются следующим образом: Закон инерции Сильвестра, а именно их положительный индекс, нулевой индекс и отрицательный индекс: квадратичная форма в п переменные могут быть преобразованы в диагональная форма, так как ${ displaystyle x_ {1} ^ {2} + x_ {2} ^ {2} + cdots + x_ {k} ^ {2} -x_ {k + 1} ^ {2} - cdots -x_ {k + ell} ^ {2},}$ где количество +1 коэффициентов, k, - положительный индекс, количество коэффициентов −1, ℓ, - отрицательный индекс, а остальные переменные - нулевой индекс м, так ${ Displaystyle к + ell + м = п.}$ В двух переменных ненулевые квадратичные формы классифицируются как:

• ${ displaystyle x ^ {2} + y ^ {2}}$ - положительно-определенный (отрицательный тоже включен), соответствующий эллипсам,
• ${ displaystyle x ^ {2}}$ - вырожденные, соответствующие параболам, и
• ${ displaystyle x ^ {2} -y ^ {2}}$ - неопределенный, соответствующий гиперболам.

В двух переменных квадратичные формы классифицируются дискриминантом, аналогично коникам, но в более высоких измерениях более полезной классификацией является определенный, (все положительные или все отрицательные), выродиться (несколько нулей) или неопределенный (сочетание положительного и отрицательного, но без нулей). Эта классификация лежит в основе многих последующих.

Кривизна

В Гауссова кривизна из поверхность описывает бесконечно малую геометрию и может в каждой точке быть положительным - эллиптическая геометрия, нуль - Евклидова геометрия (плоская, парабола) или отрицательная - гиперболическая геометрия; бесконечно мало, до второго порядка поверхность выглядит как график ${ displaystyle x ^ {2} + y ^ {2},}$ ${ displaystyle x ^ {2}}$ (или 0), или ${ displaystyle x ^ {2} -y ^ {2}}$. Действительно, по теорема униформизации любую поверхность можно считать глобально (в каждой точке) положительно изогнутой, плоской или отрицательно изогнутой. В более высоких измерениях Тензор кривизны Римана это более сложный объект, но коллекторы с постоянной секционной кривизной являются интересными объектами изучения и обладают совершенно разными свойствами, как обсуждается на секционная кривизна.

PDE второго порядка

Уравнения с частными производными (PDEs) из второго порядка классифицируются в каждой точке как эллиптические, параболические или гиперболические, соответственно, поскольку их члены второго порядка соответствуют эллиптической, параболической или гиперболической квадратичной форме. Поведение и теория этих различных типов PDE разительно различаются - характерным примером является то, что Уравнение Пуассона эллиптический, уравнение теплопроводности параболический, а волновое уравнение гиперболический.

Классификация эксцентриситета включают:

Преобразования Мебиуса

Реальные преобразования Мёбиуса (элементы PSL₂(р) или его 2-кратная крышка, SL₂(р) ) находятся классифицированный как эллиптический, параболический или гиперболический соответственно, поскольку их полуслед ${ Displaystyle 0 Leq | OperatorName {tr} | / 2 <1,}$ ${ Displaystyle | OperatorName {tr} | / 2 = 1,}$ или же ${ displaystyle | operatorname {tr} | / 2> 1,}$ зеркальное отображение классификации по эксцентриситету.

Отношение дисперсии к среднему

Отношение дисперсии к среднему классифицирует несколько важных семейств дискретные распределения вероятностей: постоянное распределение как круговое (эксцентриситет 0), биномиальные распределения как эллиптический, Распределения Пуассона как параболический, и отрицательные биномиальные распределения как гиперболический. Это подробно описано в кумулянты некоторых дискретных распределений вероятностей.

В этот интерактивный SVG, переместите влево и вправо по изображению SVG, чтобы повернуть двойной конус

Смотрите также

• Циркумконический и инконический
• Восстание конических сечений, протесты студентов Йельского университета
• Директорский кружок
• Эллиптическая система координат
• Эквидистантный набор
• Девятиконечная коническая
• Параболические координаты
• Квадратичная функция

Примечания

Рекомендации

• Акопян, А.В .; Заславский, А.А. (2007). Геометрия коник. Американское математическое общество. ISBN  978-0-8218-4323-9.
• Арци, Рафаэль (2008) [1965], Линейная геометрия, Дувр, ISBN  978-0-486-46627-9
• Бойер, Карл Б. (2004) [1956], История аналитической геометрии, Дувр, ISBN  978-0-486-43832-0
• Браннан, Дэвид А .; Эсплен, Мэтью Ф .; Грей, Джереми Дж. (1999), Геометрия, Издательство Кембриджского университета, ISBN  978-0-521-59787-6
• Кокстер, H.S.M. (1964), Проективная геометрия, Блейсделл, ISBN  9780387406237
• Кокстер, H.S.M. (1993), Реальная проективная плоскость, Springer Science & Business Media
• Даунс, Дж. (2003) [1993], Практические конические сечения: геометрические свойства эллипсов, парабол и гипербол, Дувр, ISBN  0-486-42876-1
• Евс, Ховард (1963), Обзор геометрии (Том первый), Бостон: Аллин и Бэкон
• Хартманн, Эрих, Геометрия плоского круга, введение в плоскости Мебиуса, Лагерра и Минковского (PDF), получено 20 сентября 2014 (PDF; 891 кБ).
• Кац, Виктор Дж. (1998), История математики / Введение (2-е изд.), Эддисон Уэсли Лонгман, ISBN  978-0-321-01618-8
• Кендиг, Кит (2005), Коники, Математическая ассоциация Америки, ISBN  978-0-88385-335-1
• Фолкнер, Т. Э. (1952), Проективная геометрия (2-е изд.), Эдинбург: Оливер и Бойд, ISBN  9780486154893
• Мерсерв, Брюс Э. (1983) [1959], Основные понятия геометрии, Дувр, ISBN  0-486-63415-9
• Protter, Murray H .; Морри младший, Чарльз Б. (1970), Вычисление колледжа с аналитической геометрией (2-е изд.), Литература: Эддисон-Уэсли, LCCN  76087042
• Рихтер-Геберт, Юрген (2011). Перспективы проективной геометрии: экскурсия по реальной и сложной геометрии. Springer. ISBN  9783642172854.
• Самуэль, Пьер (1988), Проективная геометрия, Тексты для бакалавриата по математике (Чтения по математике), Нью-Йорк: Springer-Verlag, ISBN  0-387-96752-4
• Томас, Джордж Б .; Финни, Росс Л. (1979), Исчисление и аналитическая геометрия (пятое изд.), Addison-Wesley, p. 434, ISBN  0-201-07540-7
• Wilson, W.A .; Трейси, Дж. (1925), Аналитическая геометрия (Пересмотренное издание), округ Колумбия Хит и компания

внешняя ссылка

• Коническое сечение (Геометрия) на Британская энциклопедия
• Можно ли вывести конические формулы из конуса? архив 2007-07-15 Гэри С. Стаудт (Индианский университет Пенсильвании
• Конические секции в Специальные плоские кривые.
• Вайсштейн, Эрик В. «Коническое сечение». MathWorld.
• Возникновение конусов. Коники в природе и в других местах.
• Видеть Конические сечения в завязать узел для точного доказательства того, что любое конечное коническое сечение является эллипсом и Кса Ли для аналогичной обработки других конусов.
• Восьмиконечная коническая в Эскизы динамической геометрии
• Локус неявного уравнения второго порядка Интерактивный графический редактор коник Java; использует общее неявное уравнение второго порядка.