График функции - Википедия - Graph of a function

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: «График функции»  – Новости  · газеты  · книги  · ученый  · JSTOR (Август 2014 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

График функции ж(Икс) = Икс³ − 9Икс

В математика, то график из функция ж это набор заказанные пары (Икс, у), куда ж(Икс) = у. В общем случае, когда Икс и ж(Икс) находятся действительные числа эти пары Декартовы координаты очков в двумерное пространство и таким образом образуют подмножество этой плоскости.

В случае функций двух переменных, то есть функций, область определения которых состоит из пар (Икс, у), график обычно относится к множеству заказал троек (Икс, у, z) куда ж(Икс, у) = z, вместо пар ((Икс, у), z) как в определении выше. Этот набор является подмножеством трехмерное пространство; для непрерывного функция с действительным знаком двух реальных переменных, это поверхность.

График функции - это частный случай связь.

В наука, инженерное дело, технологии, финансы и других областях графики - это инструменты, используемые для многих целей. В простейшем случае одна переменная отображается как функция другой, обычно с использованием прямоугольные оси; видеть Сюжет (графика) для подробностей.

В современном основы математики, и, как правило, в теория множеств, функция фактически равна своему графику.^[1] Однако часто бывает полезно рассматривать функции как сопоставления,^[2] которые состоят не только из отношения между вводом и выводом, но также из того, какой набор является доменом, а какой набор является codomain. Например, чтобы сказать, что функция находится на (сюръективный ) или не учитывать кодомен. График функции сам по себе не определяет кодомен. Это общепринято^[3] использовать оба термина функция и график функции поскольку даже если они рассматриваются как один и тот же объект, они указывают на то, что смотрят на него с другой точки зрения.

График функции ж(Икс) = Икс⁴ − 4^Икс над интервал [−2, + 3]. Также показаны два действительных корня и локальный минимум, которые находятся в интервале.

Определение

Учитывая отображение ${ displaystyle f: от X до Y}$, другими словами, функция ${ displaystyle f}$ вместе со своим доменом ${ displaystyle X}$ и codomain ${ displaystyle Y}$, график отображения^[4] набор

${ Displaystyle G (е) = {(х, е (х)) середина х в X }}$,

который является подмножеством ${ Displaystyle X раз Y}$. В абстрактном определении функции ${ Displaystyle G (f)}$ фактически равно ${ displaystyle f}$.

Можно заметить, что если ${ displaystyle f: mathbb {R} ^ {n} to mathbb {R} ^ {m}}$, то график ${ Displaystyle G (f)}$ это подмножество ${ Displaystyle mathbb {R} ^ {п + м}}$ (строго говоря это ${ Displaystyle mathbb {R} ^ {n} times mathbb {R} ^ {m}}$, но его можно вложить естественным изоморфизмом).

Примеры

Функции одной переменной

График функция ж(Икс, у) = грех (Икс²) · Cos (у²).

График функции ${ displaystyle f: {1,2,3 } к {a, b, c, d }}$ определяется

${ displaystyle f (x) = { begin {case} a, & { text {if}} x = 1, d, & { text {if}} x = 2, c, & { text {if}} x = 3, end {case}}}$

это подмножество множества ${ Displaystyle {1,2,3 } раз {а, б, в, г }}$

${ Displaystyle G (е) = {(1, а), (2, d), (3, с) }. ,}$

На графике домен ${ displaystyle {1,2,3 }}$ восстанавливается как набор первых компонентов каждой пары в графе ${ displaystyle {1,2,3 } = {x: { text {там существует}} y, { text {такой, что}} (x, y) in G (f) }}$. Точно так же классифицировать можно восстановить как ${ displaystyle {a, c, d } = {y: { text {там существует}} x, { text {такой, что}} (x, y) in G (f) }}$.Кодомен ${ Displaystyle {а, б, в, г }}$однако нельзя определить только по графику.

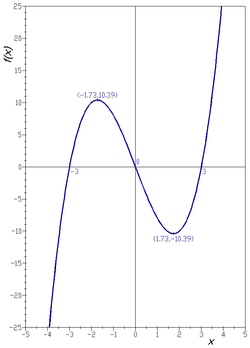
График кубического полинома на реальная линия

${ Displaystyle е (х) = х ^ {3} -9x ,}$

является

${ displaystyle {(x, x ^ {3} -9x): x { text {- действительное число}} }. ,}$

Если этот набор нанесен на декартову плоскость, результатом будет кривая (см. Рисунок).

Функции двух переменных

Сюжет графика ж(Икс, у) = - (cos (Икс²) + cos (у²))², также показывающий его градиент, спроецированный на нижнюю плоскость.

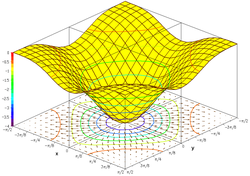
График тригонометрическая функция

${ Displaystyle е (х, у) = грех (х ^ {2}) соз (у ^ {2}) ,}$

является

${ displaystyle {(x, y, sin (x ^ {2}) cos (y ^ {2})): x { text {и}} y { text {- действительные числа}} } .}$

Если этот набор нанесен на трехмерная декартова система координат, в результате получится поверхность (см. рисунок).

Часто бывает полезно показать с графиком градиент функции и несколько кривых уровня. Кривые уровня могут быть нанесены на функциональную поверхность или могут быть спроецированы на нижнюю плоскость. На втором рисунке показан такой рисунок графика функции:

${ Displaystyle е (х, у) = - ( соз (х ^ {2}) + соз (у ^ {2})) ^ {2} ,}$

Обобщения

График функции содержится в Декартово произведение наборов. Плоскость X – Y представляет собой декартово произведение двух линий, называемых X и Y, а цилиндр - это декартово произведение прямой и окружности, высота, радиус и угол которой задают точное расположение точек. Пучки волокон не являются декартовыми произведениями, но кажутся близкими. Соответствующее понятие графа на расслоении называется графом. раздел.

Смотрите также

Рекомендации

внешняя ссылка

• Weisstein, Eric W. "График функций. »Из MathWorld - веб-ресурса Wolfram.