Тензор кривизны Римана - Википедия - Riemann curvature tensor

Часть цикла статей о
Общая теория относительности
${ Displaystyle G _ { mu nu} + Lambda g _ { mu nu} = { frac {8 pi G} {c ^ {4}}} T _ { mu nu}}$
Введение История Математическая формулировка Тесты
Основные концепции Принцип относительности Теория относительности Точка зрения Инерциальная система отсчета Рама отдыха Рамка центра импульса Световой конус Принцип эквивалентности Эквивалентность массы и энергии Специальная теория относительности Двойная специальная теория относительности инвариант де Ситтера специальная теория относительности Масштаб относительности Мировая линия Подходящее время Риманова геометрия Энергетическое состояние
Явления Гравитоэлектромагнетизм Проблема Кеплера Сила тяжести Гравитационное поле Гравитационный колодец Гравитационное линзирование Гравитационные волны Гравитационное красное смещение Красное смещение Синий сдвиг Замедление времени Гравитационное замедление времени Задержка Шапиро Гравитационный потенциал Гравитационное сжатие Гравитационный коллапс Перетаскивание кадра Геодезический эффект Видимый горизонт Горизонт событий Гравитационная сингулярность Обнаженная особенность Черная дыра Белая дыра Пространство-время Космос Время Диаграммы пространства-времени Пространство-время Минковского Замкнутая временная кривая (СТС) Червоточина Червоточина Эллиса
Уравнения Формализмы Уравнения Линеаризованная гравитация Уравнения поля Эйнштейна Фридман Геодезические Матиссон – Папапетру – Диксон Гамильтон – Якоби – Эйнштейн Инвариант кривизны (общая теория относительности) Лоренцево многообразие Формализмы ADM БССН Ньюман – Пенроуз Постньютоновский Продвинутая теория Теория Калуцы – Клейна Квантовая гравитация Супергравитация
Решения Шварцшильд (интерьер ) Рейсснер-Нордстрём Гёдель Керр Керр – Ньюман Kasner Лемэтр – Толман Тауб-ОРЕХ Milne Робертсон – Уокер pp-волна van Stockum пыль Вейль – Льюис – Папапетру Вакуумный раствор
Теоремы Теорема Биркгофа Теорема Героха о расщеплении Теорема Гольдберга – Сакса. Теорема Лавлока Теорема об отсутствии волос Теоремы Пенроуза – Хокинга об особенностях Теорема положительной энергии
Ученые Эйнштейн Лоренц Гильберта Пуанкаре Шварцшильд де Ситтер Рейсснер Nordström Weyl Эддингтон Фридман Milne Цвикки Лемэтр Гёдель Уиллер Робертсон Бардин Уокер Керр Чандрасекхар Элерс Пенроуз Хокинг Райчаудхури Тейлор Hulse van Stockum Тауб Новый человек Яу Торн другие

в математический поле дифференциальная геометрия, то Тензор кривизны Римана или Тензор Римана – Кристоффеля (после Бернхард Риманн и Элвин Бруно Кристоффель ) является наиболее распространенным способом выражения кривизна римановых многообразий. Он присваивает тензор в каждую точку Риманово многообразие (т.е. это тензорное поле ), который измеряет степень, в которой метрический тензор не является локально изометричным пространству Евклида. Тензор кривизны также можно определить для любого псевдориманово многообразие, или любой другой коллектор, оснащенный аффинная связь.

Это центральный математический инструмент в теории общая теория относительности, современная теория сила тяжести, а кривизна пространство-время в принципе наблюдается через уравнение геодезического отклонения. Тензор кривизны представляет собой приливная сила испытываемый твердым телом, движущимся по геодезический в некотором смысле, уточненном Уравнение Якоби.

Этот тензор кривизны задается в терминах Леви-Чивита связь ${ displaystyle nabla}$ по следующей формуле:

${ Displaystyle Р (и, v) вес = набла _ {и} набла _ {v} ш- набла _ {v} набла _ {и} ш- набла _ {[и, v]} ш }$

или эквивалентно

${ displaystyle R (u, v) = [ nabla _ {u}, nabla _ {v}] - nabla _ {[u, v]}}$

где [ты, v] это Скобка Ли векторных полей и ${ displaystyle [ nabla _ {u}, nabla _ {v}]}$ является коммутатором дифференциальных операторов. Для каждой пары касательных векторов ты, v, р(ты, v) является линейным преобразованием касательного пространства многообразия. Это линейно по ты и v, и таким образом определяет тензор. Иногда тензор кривизны определяется с противоположным знаком.

Если ${ Displaystyle и = partial / partial х ^ {я}}$ и ${ Displaystyle v = partial / partial x ^ {j}}$ координатные векторные поля, то ${ Displaystyle [и, v] = 0}$ и поэтому формула упрощается до

${ displaystyle R (u, v) w = nabla _ {u} nabla _ {v} w- nabla _ {v} nabla _ {u} w.}$

Тензорные меры кривизны некоммутативность ковариантной производной, и как таковой препятствие интегрируемости для существования изометрии с евклидовым пространством (называемой в этом контексте плоский Космос). Линейное преобразование ${ Displaystyle ш mapsto R (и, v) ш}$ также называется преобразование кривизны или эндоморфизм.

Формулу кривизны также можно выразить через вторая ковариантная производная определяется как:^[1]

${ displaystyle nabla _ {u, v} ^ {2} w = nabla _ {u} nabla _ {v} w- nabla _ { nabla _ {u} v} w}$

что линейно по ты и v. Потом:

${ displaystyle R (u, v) = nabla _ {u, v} ^ {2} - nabla _ {v, u} ^ {2}}$

Таким образом, в общем случае некоординатных векторов ты и vтензор кривизны измеряет некоммутативность второй ковариантной производной.

Геометрический смысл

Иллюстрация мотивации кривизны Римана на сфера -подобное многообразие. Тот факт, что этот перенос может определять два разных вектора в начальной точке, приводит к появлению тензора кривизны Римана. В прямой угол символ означает, что внутренний продукт (предоставлено метрический тензор ) между перемещаемыми векторами (или касательными векторами кривых) равно 0.

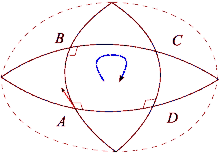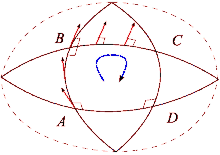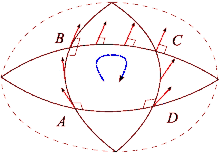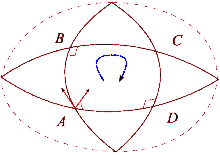
Неформально

Эффект искривления пространства можно увидеть, сравнив теннисный корт и Землю. Начните с правого нижнего угла теннисного корта с ракеткой, вытянутой к северу. Затем, прогуливаясь по контуру площадки, на каждом шаге следите за тем, чтобы теннисная ракетка находилась в той же ориентации, параллельно ее предыдущему положению. По завершении петли теннисная ракетка будет параллельна своему исходному положению. Это потому, что теннисные корты построены с ровной поверхностью. С другой стороны, поверхность Земли изогнута: мы можем образовать петлю на поверхности Земли. Начиная с экватора, направьте теннисную ракетку на север по поверхности Земли. Еще раз, теннисная ракетка всегда должна оставаться параллельной своему предыдущему положению, используя локальную плоскость горизонта в качестве ориентира. Для этого пути сначала пройдите к северному полюсу, затем поверните на 90 градусов и спуститесь к экватору, и, наконец, поверните на 90 градусов и вернитесь к началу. Однако теперь теннисная ракетка будет направлена ​​назад (на восток). Этот процесс сродни параллельная транспортировка вектор вдоль пути, и разница определяет, как линии, которые кажутся "прямыми", являются "прямыми" только локально. Каждый раз, когда петля будет завершена, теннисная ракетка будет отклоняться от своего исходного положения на величину, зависящую от расстояния и кривизны поверхности. Можно определить пути вдоль изогнутой поверхности, где работает параллельный транспорт, так же, как и на ровном пространстве. Эти геодезический пространства, например любой отрезок большого круга сферы.

Концепция искривленного пространства в математике отличается от разговорного использования. Например, если описанный выше процесс был завершен на цилиндре, можно было бы обнаружить, что он не изогнут в целом, поскольку кривизна вокруг цилиндра компенсируется плоскостностью вдоль цилиндра, это является следствием Гауссова кривизна и Теорема Гаусса – Бонне. Знакомый пример этого - гибкий кусок пиццы, который останется жестким по длине, если он будет изогнут по ширине.

Тензор кривизны Римана - это способ определить меру внутренней кривизны. Когда вы записываете его в терминах его компонентов (например, записываете компоненты вектора), он состоит из многомерного массива сумм и произведений частных производных (некоторые из этих частных производных можно рассматривать как сродни захвату кривизна, накладываемая на человека, идущего по прямой линии по изогнутой поверхности).

Формально

Когда вектор в евклидовом пространстве равен параллельно транспортируется вокруг петли, он снова будет указывать в исходном направлении после возврата в исходное положение. Однако в общем случае это свойство не выполняется. Тензор кривизны Римана непосредственно измеряет несостоятельность этого в общем случае. Риманово многообразие. Этот сбой известен как не-голономия коллектора.

Позволять Икс_т кривая на римановом многообразии M. Обозначим через τ_Икст : Т_Икс0M → Т_ИкстM параллельная транспортная карта вдоль Икс_т. Карты параллельного транспорта связаны с ковариантная производная от

${ displaystyle nabla _ {{ dot {x}} _ {0}} Y = lim _ {h to 0} { frac {1} {h}} left (Y_ {x_ {0}} - tau _ {x_ {h}} ^ {- 1} left (Y_ {x_ {h}} right) right) = left. { frac {d} {dt}} left ( tau _ {x_ {t}} Y right) right | _ {t = 0}}$

для каждого векторное поле Y определяется вдоль кривой.

Предположим, что Икс и Y - пара коммутирующих векторных полей. Каждое из этих полей порождает однопараметрическую группу диффеоморфизмов в окрестности Икс₀. Обозначим через τ_tX и τ_tYсоответственно, параллельные переносы по потокам Икс и Y На время т. Параллельный перенос вектора Z ∈ T_Икс0M вокруг четырехугольника со сторонами tY, sX, −tY, −sX дан кем-то

${ displaystyle tau _ {sX} ^ {- 1} tau _ {tY} ^ {- 1} tau _ {sX} tau _ {tY} Z.}$

Это измеряет отказ параллельного транспорта для возврата Z в исходное положение в касательном пространстве T_Икс0M. Уменьшение цикла путем отправки s, т → 0 дает бесконечно малое описание этого отклонения:

${ displaystyle left. { frac {d} {ds}} { frac {d} {dt}} tau _ {sX} ^ {- 1} tau _ {tY} ^ {- 1} tau _ {sX} tau _ {tY} Z right | _ {s = t = 0} = left ( nabla _ {X} nabla _ {Y} - nabla _ {Y} nabla _ {X } - nabla _ {[X, Y]} right) Z = R (X, Y) Z}$

где р - тензор кривизны Римана.

Координатное выражение

Преобразование в обозначение тензорного индекса, тензор кривизны Римана имеет вид

${ Displaystyle R ^ { rho} {} _ { sigma mu nu} = dx ^ { rho} left (R left ( partial _ { mu}, partial _ { nu} справа) partial _ { sigma} right)}$

где ${ Displaystyle partial _ { mu} = partial / partial x ^ { mu}}$ - координатные векторные поля. Вышеприведенное выражение можно записать с помощью Символы Кристоффеля:

${ Displaystyle R ^ { rho} {} _ { sigma mu nu} = partial _ { mu} Gamma ^ { rho} {} _ { nu sigma} - partial _ { nu} Gamma ^ { rho} {} _ { mu sigma} + Gamma ^ { rho} {} _ { mu lambda} Gamma ^ { lambda} {} _ { nu sigma } - Gamma ^ { rho} {} _ { nu lambda} Gamma ^ { lambda} {} _ { mu sigma}}$

(см. также список формул в римановой геометрии ).

Тензор кривизны Римана также является коммутатор ковариантной производной произвольного ковектора ${ displaystyle A _ { nu}}$ с собой:^[2][3]

${ Displaystyle A _ { nu; sigma rho} -A _ { nu; rho sigma} = - A _ { beta} R ^ { beta} {} _ { nu rho sigma},}$

так как связь ${ displaystyle Gamma ^ { alpha} {} _ { beta mu}}$ без кручения, что означает, что тензор кручения ${ displaystyle Gamma ^ { lambda} {} _ { mu nu} - Gamma ^ { lambda} {} _ { nu mu}}$ исчезает.

Эту формулу часто называют Личность Риччи.^[4] Это классический метод, используемый Риччи и Леви-Чивита чтобы получить выражение для тензора кривизны Римана.^[5] Таким образом, тензорный характер множества величин ${ Displaystyle R ^ { beta} {} _ { nu rho sigma}}$ доказано.

Это тождество можно обобщить, чтобы получить коммутаторы для двух ковариантных производных произвольных тензоров следующим образом ^[6]

${ displaystyle { begin {align} & nabla _ { delta} nabla _ { gamma} T ^ { alpha _ {1} cdots alpha _ {r}} {} _ { beta _ { 1} cdots beta _ {s}} - nabla _ { gamma} nabla _ { delta} T ^ { alpha _ {1} cdots alpha _ {r}} {} _ { beta _ {1} cdots beta _ {s}} [3pt] = {} & R ^ { alpha _ {1}} {} _ { rho delta gamma} T ^ { rho alpha _ {2} cdots alpha _ {r}} {} _ { beta _ {1} cdots beta _ {s}} + ldots + R ^ { alpha _ {r}} {} _ { rho delta gamma} T ^ { alpha _ {1} cdots alpha _ {r-1} rho} {} _ { beta _ {1} cdots beta _ {s}} - R ^ { sigma} {} _ { beta _ {1} delta gamma} T ^ { alpha _ {1} cdots alpha _ {r}} {} _ { sigma beta _ {2} cdots beta _ {s}} - ldots -R ^ { sigma} {} _ { beta _ {s} delta gamma} T ^ { alpha _ {1} cdots alpha _ {r} } {} _ { beta _ {1} cdots beta _ {s-1} sigma} end {align}}}$

Эта формула также применима к тензорные плотности без изменений, потому что для Levi-Civita (не общий) соединение получается:^[4]

${ displaystyle nabla _ { mu} left ({ sqrt {g}} right) Equiv left ({ sqrt {g}} right) _ {; mu} = 0,}$

где

${ Displaystyle g = left | det left (g _ { mu nu} right) right |.}$

Иногда удобно также определить чисто ковариантную версию с помощью

${ Displaystyle R _ { rho sigma mu nu} = g _ { rho zeta} R ^ { zeta} {} _ { sigma mu nu}.}$

Симметрии и идентичности

Тензор кривизны Римана обладает следующими симметриями:

${ Displaystyle { begin {align} R (u, v) & = - R (v, u) langle R (u, v) w, z rangle & = - langle R (u, v) z, w rangle R (u, v) w + R (v, w) u + R (w, u) v & = 0. end {align}}}$

Здесь скобка ${ displaystyle langle, rangle}$ относится к внутреннему произведению на касательном пространстве, индуцированном метрический тензор. Последняя личность была обнаружена Риччи, но его часто называют первая личность Бианки или алгебраическое тождество Бьянки, потому что он похож на Bianchi личность ниже. (Также, если есть ненулевое кручение, первое тождество Бианки становится дифференциальным тождеством тензор кручения.) Эти три тождества образуют полный список симметрий тензора кривизны, т.е. для любого тензора, удовлетворяющего указанным выше тождествам, можно найти риманово многообразие с таким тензором кривизны в некоторой точке. Несложные вычисления показывают, что такой тензор имеет ${ Displaystyle п ^ {2} влево (п ^ {2} -1 вправо) / 12}$ независимые компоненты.^[7]

Еще одна полезная идентичность следует из этих трех:

${ Displaystyle langle R (u, v) w, z rangle = langle R (w, z) u, v rangle.}$

На римановом многообразии имеется ковариантная производная ${ displaystyle nabla _ {u} R}$ и Бьянки идентичность (часто называемое вторым тождеством Бьянки или дифференциальным тождеством Бьянки) принимает форму:

${ displaystyle left ( nabla _ {u} R right) (v, w) + left ( nabla _ {v} R right) (w, u) + left ( nabla _ {w} R right) (u, v) = 0.}$

Учитывая любые карта координат относительно некоторой точки многообразия, указанные выше тождества могут быть записаны в терминах компонент тензора Римана в этой точке как:

Косая симметрия

${ displaystyle R_ {abcd} = - R_ {bacd} = - R_ {abdc}}$

Симметрия обмена

${ Displaystyle R_ {abcd} = R_ {cdab}}$

Первое (алгебраическое) тождество Бьянки

$${ displaystyle R_ {abcd} + R_ {acdb} + R_ {adbc} = 0}$$

Об этом часто пишут:

$${ displaystyle R_ {a [bcd]} = 0,}$$

где скобки обозначают антисимметричная часть по указанным показателям. Это эквивалентно предыдущей версии тождества, потому что тензор Римана уже перекос по своим последним двум индексам.

Вторая (дифференциальная) идентичность Бьянки

$${ Displaystyle R_ {abcd; e} + R_ {abde; c} + R_ {abec; d} = 0}$$

Точка с запятой обозначает ковариантную производную. Эквивалентно,

$${ displaystyle R_ {ab [cd; e]} = 0}$$

снова используя антисимметрию на последних двух индексах р.

Алгебраические симметрии также эквивалентны утверждению, что р принадлежит имиджу Юный симметризатор соответствующий разбиению 2 + 2.

Кривизна Риччи

В Кривизна Риччи тензор - это сжатие первого и третьего индексов тензора Римана.

${ displaystyle underbrace { operatorname {R} _ {ab}} _ { text {Ricci}} Equiv underbrace { operatorname {R} ^ {c} {} _ {acb}} _ { text { Риман}} = g ^ {cd} underbrace { operatorname {R} _ {cadb}} _ { text {Riemann}}}$

Особые случаи

Поверхности

Для двумерного поверхность, тождества Бианки означают, что тензор Римана имеет только одну независимую компоненту, что означает, что скаляр Риччи полностью определяет тензор Римана. Существует только одно допустимое выражение для тензора Римана, которое соответствует требуемой симметрии:

${ Displaystyle R_ {abcd} = f (R) left (g_ {ac} g_ {db} -g_ {ad} g_ {cb} right) ,}$

и, дважды сжимая метрику, мы находим явный вид:

${ displaystyle R_ {abcd} = K left (g_ {ac} g_ {db} -g_ {ad} g_ {cb} right) ,}$

где ${ displaystyle g_ {ab}}$ это метрический тензор и ${ Displaystyle К = R / 2}$ функция, называемая Гауссова кривизна и а, б, c и d принимают значения либо 1, либо 2. Тензор Римана имеет только одну функционально независимую компоненту. Гауссова кривизна совпадает с секционная кривизна поверхности. Это также ровно половина скалярная кривизна двумерного многообразия, а Кривизна Риччи тензор поверхности просто дается

${ displaystyle operatorname {R} _ {ab} = кг_ {ab}. ,}$

Космические формы

Риманово многообразие - это космическая форма если это секционная кривизна равна константе K. Тензор Римана пространственной формы задается формулой

${ displaystyle R_ {abcd} = K left (g_ {ac} g_ {db} -g_ {ad} g_ {cb} right).}$

Наоборот, за исключением размерности 2, если кривизна риманова многообразия имеет такой вид для некоторой функции K, то из тождеств Бьянки следует, что K постоянна и, следовательно, многообразие является (локально) пространственной формой.

Смотрите также

• Введение в математику общей теории относительности
• Разложение тензора кривизны Римана
• Кривизна римановых многообразий
• Тензор кривизны Риччи

Заметки

использованная литература

• Бесс, А. Л. (1987), Многообразия Эйнштейна, Спрингер, ISBN  0-387-15279-2
• Кобаяши, С .; Номидзу, К. (1963), Основы дифференциальной геометрии, 1, Interscience
• Миснер, Чарльз В.; Торн, Кип С.; Уилер, Джон А. (1973), Гравитация, У. Х. Фриман, ISBN  978-0-7167-0344-0