Кривизна - Curvature
В математика, кривизна является одним из нескольких тесно связанных понятий в геометрия. Интуитивно, кривизна - это величина, на которую кривая отклоняется от того, чтобы быть прямая линия, или поверхность отклоняется от того, чтобы быть самолет.
Для кривых каноническим примером является круг, имеющий кривизну, равную взаимный своего радиус. Меньшие круги изгибаются более резко и, следовательно, имеют большую кривизну. Кривизна в какой-то момент из дифференцируемая кривая кривизна его соприкасающийся круг, то есть круг, который наилучшим образом аппроксимирует кривую около этой точки. Кривизна прямой равна нулю. Кривизна кривой в точке обычно равна скаляр количество, то есть выражается одним настоящий номер.
Для поверхностей (и, в более общем смысле, для многомерных коллекторы ), которые встроенный в Евклидово пространство, понятие кривизны более сложное, поскольку оно зависит от выбора направления на поверхности или многообразии. Это приводит к концепции максимальная кривизна, минимальная кривизна, и средняя кривизна.
Для Римановы многообразия (размерности не менее двух), которые не обязательно вложены в евклидово пространство, можно определить кривизну по сути, то есть без обращения к внешнему пространству. Увидеть Кривизна римановых многообразий для определения, которое делается в терминах длин кривых, начерченных на многообразии, и выражается с помощью линейная алгебра, посредством Тензор кривизны Римана.
История
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Октябрь 2019) |
В Tractatus de configurationibus qualitatum et motuum[1] философ и математик 14 векаНиколь Орем вводит понятие кривизны как меры отклонения от прямолинейности, для окружностей он имеет кривизну, обратно пропорциональную радиусу, и пытается распространить ее на другие кривые в виде непрерывно меняющейся величины. [2]
Кривизна дифференцируемая кривая изначально был определен через соприкасающиеся круги. В этой настройке Огюстен-Луи Коши показал, что центр кривизны - это точка пересечения двух бесконечно близких нормальные линии к кривой.[3]
Плоские кривые
Интуитивно кривизна описывает для любой части кривой, насколько направление кривой изменяется на небольшом пройденном расстоянии (например, угол в рад / м), так что это мера мгновенная скорость изменения из направление точки, которая движется по кривой: чем больше кривизна, тем больше скорость изменения. Другими словами, кривизна измеряет, насколько быстро вращается единичный касательный вектор к кривой.[4] (быстро с точки зрения положения кривой). Фактически, можно доказать, что эта мгновенная скорость изменения и есть кривизна. Точнее, предположим, что точка движется по кривой с постоянной скоростью в одну единицу, то есть положение точки п(s) является функцией параметра s, который можно рассматривать как время или как длина дуги из заданного происхождения. Позволять Т(s) быть единичный касательный вектор кривой на п(s), который также является производная из п(s) относительно s. Тогда производная от Т(s) относительно s - вектор, нормальный к кривой, длина которого равна кривизне.
Для того чтобы иметь смысл, определение кривизны и ее различных характеристик требует, чтобы кривая непрерывно дифференцируемый около п, за наличие касательной, которая непрерывно изменяется; требуется также, чтобы кривая была дважды дифференцируемой в точке п, для обеспечения существования задействованных лимитов и производной от Т(s).
Определение кривизны в терминах производной единичного касательного вектора, вероятно, менее интуитивно понятно, чем определение в терминах соприкасающейся окружности, но формулы для вычисления кривизны легче вывести. Поэтому, а также из-за его использования в кинематика, эту характеристику часто дают как определение кривизны.
Оскулирующий круг
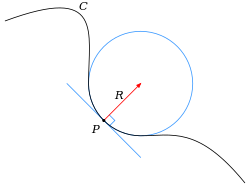
Исторически кривизна дифференцируемой кривой определялась через соприкасающийся круг, представляющий собой круг, который наилучшим образом аппроксимирует кривую в точке. Точнее с учетом балла п на кривой, все остальные точки Q кривой определяет окружность (или иногда линию), проходящую через Q и касательная к кривой на п. Окуляционный круг - это предел, если он существует, этого круга, когда Q как правило п. Тогда центр и радиус кривизны кривой на п центр и радиус соприкасающегося круга. Кривизна - это взаимный радиуса кривизны. То есть кривизна
где р это радиус кривизны[5] (весь круг имеет эту кривизну, это можно прочитать как поворот 2π по длине 2πр).
Этим определением сложно манипулировать и выразить его формулами. Поэтому были введены другие эквивалентные определения.
С точки зрения параметризации длины дуги
Каждые дифференцируемая кривая может быть параметризованный относительно длина дуги.[6] В случае плоской кривой это означает наличие параметризации γ(s) = (Икс(s), у(s)), где Икс и у - действительные дифференцируемые функции, производные которых удовлетворяют
Это означает, что касательный вектор
имеет норму, равную единице, и, следовательно, является единичный касательный вектор.
Если кривая дважды дифференцируема, то есть если вторые производные от Икс и у существуют, то производная от Т(s) существуют. Этот вектор нормален к кривой, его нормой является кривизна κ(s), и он ориентирован к центру кривизны. Это,
Более того, поскольку радиус кривизны
а центр кривизны - перпендикулярно кривой, центр кривизны - точка
Если N(s) это единичный вектор нормали получен из Т(s) вращением против часовой стрелки π/2, тогда
с участием k(s) = ± κ(s). Настоящее число k(s) называется ориентированный или знаковая кривизна. Это зависит как от ориентации плоскости (определение против часовой стрелки), так и от ориентации кривой, обеспечиваемой параметризацией. Фактически, изменение переменной s → –s обеспечивает другую параметризацию длины дуги и меняет знак k(s).
С точки зрения общей параметризации
Позволять γ(т) = (Икс(т), у(т)) быть правильным параметрическое представление дважды дифференцируемой плоской кривой. Вот правильный означает, что на домен определения параметризации, производная dγ/dtопределен, дифференцируем и нигде не равен нулевому вектору.
При такой параметризации кривизна со знаком равна
где штрихи относятся к производным по т. Кривизна κ таким образом
Они могут быть выражены безкоординатным образом как
Эти формулы могут быть получены из частного случая параметризации длины дуги следующим образом. Из приведенного выше условия параметризации следует, что длина дуги s дифференцируемый монотонная функция параметра т, и наоборот, что т является монотонной функцией s. Более того, изменив при необходимости s к –s, можно предположить, что эти функции возрастают и имеют положительную производную. Используя обозначения предыдущего раздела и Правило цепи, надо
и, таким образом, принимая норму обеих сторон
где штрих означает вывод по т.
Кривизна - это норма производной от Т относительно s. Используя приведенную выше формулу и цепное правило, эту производную и ее норму можно выразить через γ′ и γ″ только с параметром длины дуги s полностью исключили, дав приведенные выше формулы для кривизны.
График функции
В график функции у = ж(Икс), является частным случаем параметризованной кривой вида
Как первая и вторая производные от Икс равны 1 и 0, предыдущие формулы упрощаются до
для кривизны, и для
для подписанной кривизны.
В общем случае кривой знак кривизны со знаком как-то произвольный, так как он зависит от ориентации кривой. В случае графика функции существует естественная ориентация за счет увеличения значений Икс. Это делает значимым признак подписанной кривизны.
Знак кривизны со знаком такой же, как и знак второй производной от ж. Если он положительный, то график имеет вогнутость вверх, а если он отрицательный, график имеет вогнутость вниз. Это ноль, значит, есть точка перегиба или точка волнистости.
Когда наклон графика (то есть производной функции) мала, кривизна со знаком хорошо аппроксимируется второй производной. Точнее, используя нотация большой O, надо
Это распространено в физика и инженерное дело аппроксимировать кривизну второй производной, например, в теория пучка или для получения волновое уравнение натянутой струны и другие приложения, где задействованы небольшие уклоны. Это позволяет часто рассматривать как линейный системы, которые в противном случае являются нелинейными.
Полярные координаты
Если кривая определена в полярные координаты радиусом, выраженным как функция полярного угла, т. е. р является функцией θ, то его кривизна равна
где штрих относится к дифференцированию по θ.
Это следует из формулы для общих параметризаций с учетом параметризации
Неявная кривая
Для кривой, определяемой неявное уравнение F(Икс, у) = 0 с участием частные производные обозначенный FИкс, Fу, Fхх, Fху, Fгг, кривизна определяется выражением[7]
Кривизна со знаком не определена, так как она зависит от ориентации кривой, которая не обеспечивается неявным уравнением. Кроме того, изменение F в –F не меняет кривую, но меняет знак числителя, если абсолютное значение опущено в предыдущей формуле.
Точка кривой, где FИкс = Fу = 0 это особая точка, что означает, что кривая не дифференцируема в этой точке, и, таким образом, кривизна не определена (чаще всего точка является либо точкой пересечения, либо куспид ).
Вышеупомянутая формула для кривизны может быть получена из выражения кривизны графика функции с помощью теорема о неявной функции и тот факт, что на такой кривой
Примеры
Может быть полезно проверить на простых примерах, что разные формулы, приведенные в предыдущих разделах, дают одинаковый результат.
Круг
Общая параметризация круг радиуса р является γ(т) = (р потому что т, р грех т). Формула кривизны дает
Из этого следует, как и ожидалось, что радиус кривизны - это радиус окружности, а центр кривизны - это центр окружности.
Круг - это редкий случай, когда параметризацию длины дуги легко вычислить, так как это
Это параметризация длины дуги, поскольку норма
равно единице. Эта параметризация дает то же значение для кривизны, что и деление на р3 в числителе и знаменателе предыдущей формулы.
Тот же круг также можно определить неявным уравнением F(Икс, у) = 0 с участием F(Икс, у) = Икс2 + у2 – р2. Тогда формула кривизны в этом случае дает
Парабола
Рассмотрим парабола у = топор2 + bx + c.
Это график функции с производной 2топор + б, и вторая производная 2а. Итак, кривизна со знаком
Имеет знак а для всех значений Икс. Это означает, что если а > 0, вогнутость всюду направлена вверх; если а < 0, вогнутость направлена вниз; для а = 0кривизна везде равна нулю, что подтверждает вырождение параболы в прямую.
(Беззнаковая) кривизна максимальна для Икс = –б/2а, то есть на стационарный пункт (нулевая производная) функции, которая является вершина параболы.
Рассмотрим параметризацию γ(т) = (т, в2 + bt + c) = (Икс, у). Первая производная от Икс является 1, а вторая производная равна нулю. Подстановка в формулу для общих параметризаций дает точно такой же результат, как и выше, с Икс заменяется т. Если использовать простые числа для производных по параметру т.
Та же парабола также может быть определена неявным уравнением F(Икс, у) = 0 с участием F(Икс, у) = топор2 + bx + c – у. Так как Fу = –1, и Fгг = Fху = 0, можно получить точно такое же значение для (беззнаковой) кривизны. Однако знаковая кривизна здесь бессмысленна, так как –F(Икс, у) = 0 является действительным неявным уравнением для той же параболы, которая дает противоположный знак кривизне.
Формулы Френе – Серре для плоских кривых.

Выражение кривизны С точки зрения параметризации длины дуги по сути первая формула Френе – Серре
где штрихи относятся к производным по длине дуги s, и N(s) нормальный единичный вектор в направлении Т′ (S).
Поскольку плоские кривые имеют ноль кручение, вторая формула Френе – Серре дает соотношение
Для общей параметризации параметром т, нужны выражения, содержащие производные по т. Поскольку они получены умножением на ds/dt производные по s, для любой правильной параметризации
Космические кривые

Как и в случае кривых в двух измерениях, кривизна регулярного пространственная кривая C в трех измерениях (и выше) - это величина ускорения частицы, движущейся с единичной скоростью по кривой. Таким образом, если γ(s) является параметризацией длины дуги C то единичный касательный вектор Т(s) дан кем-то
а кривизна - это величина ускорения:
Направление ускорения - это единичный вектор нормали N(s), который определяется
Плоскость, содержащая два вектора Т(s) и N(s) это соприкасающаяся плоскость к кривой на γ(s). Кривизна имеет следующую геометрическую интерпретацию. В соприкасающейся плоскости существует окружность, касательная к γ(s) чей ряд Тейлора до второго порядка в точке соприкосновения совпадает с рядом γ(s). Это соприкасающийся круг к кривой. Радиус круга р(s) называется радиус кривизны, а кривизна обратна радиусу кривизны:
Касательная, кривизна и вектор нормали вместе описывают поведение кривой второго порядка вблизи точки. В трехмерном пространстве поведение кривой третьего порядка описывается родственным понятием кручение, который измеряет степень, в которой кривая имеет тенденцию двигаться по спиральной траектории в пространстве. Кручение и кривизна связаны соотношением Формулы Френе – Серре (в трех измерениях) и их обобщение (в более высоких измерениях).
Общие выражения
Для параметрически определенной пространственной кривой в трех измерениях, заданных в декартовых координатах формулой γ(т) = (Икс(т), у(т), z(т)), кривизна
где штрих означает дифференцирование по параметру т. Это можно выразить независимо от системы координат с помощью формулы
где × обозначает векторное произведение. Эквивалентно,
Здесь T обозначает матрица транспонировать. Эта последняя формула (без перекрестного произведения) также верна для кривизны кривых в евклидовом пространстве любой размерности.
Кривизна от дуги и длины хорды
Учитывая два очка п и Q на C, позволять s(п,Q) быть длиной дуги участка кривой между п и Q и разреши d(п,Q) обозначают длину отрезка от п к Q. Кривизна C в п дается пределом[нужна цитата ]
где предел взят за точку Q подходы п на C. Знаменатель также можно принять равным d(п,Q)3. Формула действительна в любом измерении. Кроме того, если рассматривать предел независимо по обе стороны от п, это определение кривизны иногда может включать особенность на п. Формула следует путем проверки ее на соприкасающийся круг.
Поверхности
Кривизна кривых, нарисованных на поверхность является основным инструментом для определения и изучения кривизны поверхности.
Кривые на поверхностях
Для кривой, нарисованной на поверхности (встроенной в трехмерную Евклидово пространство ) определены несколько кривизны, которые связывают направление кривизны с единицей поверхности нормальный вектор, в том числе:
Любая неособая кривая на гладкой поверхности имеет касательный вектор Т содержится в касательная плоскость поверхности. В нормальная кривизна, kп, - кривизна кривой, спроецированной на плоскость, содержащую касательную к кривой Т и нормаль к поверхности ты; то геодезическая кривизна, kг, - кривизна кривой, спроецированной на касательную плоскость поверхности; и геодезическое кручение (или относительное кручение), τр, измеряет скорость изменения нормали к поверхности вокруг касательной к кривой.
Пусть кривая будет параметризованная длина дуги, и разреши т = ты × Т так что Т, т, ты для мужчины ортонормированный базис, называется Рамка Дарбу. Вышеуказанные количества связаны между собой:
Основная кривизна

Все кривые на поверхности с одинаковым касательным вектором в данной точке будут иметь одинаковую нормальную кривизну, которая совпадает с кривизной кривой, полученной пересечением поверхности с плоскостью, содержащей Т и ты. Взяв все возможные касательные векторы, максимальное и минимальное значения нормальной кривизны в точке называются основные кривизны, k1 и k2, а направления соответствующих касательных векторов называются основные нормальные направления.
Нормальные разделы
Кривизну можно оценить по поверхности нормальные разделы, похожий на § Кривые на поверхностях выше (см., например, Радиус кривизны Земли ).
Гауссова кривизна
В отличие от кривых, которые не имеют собственной кривизны, но имеют внешнюю кривизну (у них есть только кривизна, заданная вложением), поверхности могут иметь внутреннюю кривизну, независимо от вложения. В Гауссова кривизна, названный в честь Карл Фридрих Гаусс, равна произведению главных кривизны, k1k2. Имеет размер длины−2 и положительно для сферы, негатив для одного листа гиперболоиды и ноль для самолетов. Он определяет, является ли поверхность локально выпуклый (когда он положительный) или локально седловидный (когда отрицательный).
Гауссова кривизна - это внутренний свойства поверхности, то есть не зависит от конкретного встраивание поверхности; интуитивно это означает, что муравьи, живущие на поверхности, могут определять гауссову кривизну. Например, муравей, живущий на сфере, может измерить сумму внутренних углов треугольника и определить, что он больше 180 градусов, подразумевая, что пространство, в котором он обитает, имеет положительную кривизну. С другой стороны, муравей, живущий на цилиндре, не обнаружит такого отклонения от Евклидова геометрия; в частности, муравей не смог обнаружить, что две поверхности имеют разную среднюю кривизну (см. ниже), что является чисто внешним типом кривизны.
Формально гауссова кривизна зависит только от Риманова метрика поверхности. Это Гаусс знаменитый Теорема Egregium, который он обнаружил, занимаясь географическими съемками и картографированием.
Внутреннее определение гауссовой кривизны в точке п заключается в следующем: представьте муравья, привязанного к п с короткой нитью длины р. Это бегает вокруг п при этом нить полностью натянута и измеряет длину C(р) одного полного путешествия вокруг п. Если бы поверхность была плоской, муравей нашел бы C(р) = 2πр. На криволинейных поверхностях формула для C(р) будет другой, а гауссова кривизна K в момент п можно вычислить Теорема Бертрана – Диге – Пюизо так как
В интеграл гауссовой кривизны по всей поверхности тесно связана с ее Эйлерова характеристика; увидеть Теорема Гаусса – Бонне.
Дискретный аналог кривизны, соответствующий сосредоточению кривизны в точке и особенно полезный для многогранники, это (угловой) дефект; аналог для Теорема Гаусса – Бонне является Теорема Декарта о полном угловом дефекте.
Поскольку (гауссова) кривизна может быть определена без ссылки на пространство вложения, нет необходимости, чтобы поверхность была вложена в пространство более высокой размерности, чтобы быть искривленной. Такая искривленная двумерная поверхность является простым примером Риманово многообразие.
Средняя кривизна
Средняя кривизна - это внешний мера кривизны, равная половине суммы основные кривизны, k1 + k2/2. Имеет размер длины−1. Средняя кривизна тесно связана с первым вариантом площадь поверхности. В частности, минимальная поверхность например, мыльная пленка имеет нулевую среднюю кривизну и мыльный пузырь имеет постоянную среднюю кривизну. В отличие от кривизны Гаусса, средняя кривизна является внешней и зависит от вложения, например, цилиндр и самолет локально изометрический но средняя кривизна плоскости равна нулю, а кривизна цилиндра отлична от нуля.
Вторая фундаментальная форма
Внутренняя и внешняя кривизна поверхности может быть объединена во второй фундаментальной форме. Это квадратичная форма в касательной плоскости к поверхности в точке, значение которой в конкретном касательном векторе Икс к поверхности - нормальная составляющая ускорения кривой вдоль поверхности, касательной к Икс; то есть, это нормальная кривизна кривой, касательной к Икс (увидеть над ). Символично,
где N - единица измерения, нормальная к поверхности. Для единичных касательных векторов Икс, вторая фундаментальная форма принимает максимальное значение k1 и минимальное значение k2, которые происходят в основных направлениях ты1 и ты2соответственно. Таким образом, теорема о главной оси, вторая фундаментальная форма
Таким образом, вторая фундаментальная форма кодирует как внутреннюю, так и внешнюю кривизну.
Оператор формы
Инкапсуляцию кривизны поверхности можно найти в операторе формы, S, который является самосопряженный линейный оператор от касательной плоскости к себе (в частности, дифференциал Карта Гаусса ).
Для поверхности с касательными векторами Икс и нормально N, оператор формы можно компактно выразить в виде обозначение суммирования индексов так как
(Сравните альтернативное выражение кривизны для плоской кривой.)
В Уравнения Вейнгартена дать значение S через коэффициенты первый и вторые основные формы так как
Основные изгибы - это собственные значения оператора формы основными направлениями кривизны являются его собственные векторы кривизна Гаусса - это его детерминант, а средняя кривизна вдвое меньше след.
Искривление пространства
Расширяя предыдущий аргумент, пространство трех или более измерений может быть искривлено по своей сути. Кривизна внутренний в том смысле, что это свойство, определенное в каждой точке пространства, а не свойство, определенное по отношению к большему пространству, которое его содержит. В общем, искривленное пространство может или не может рассматриваться как встроенное в многомерный окружающее пространство; в противном случае его кривизну можно определить только внутренне.
После открытия внутреннего определения кривизны, которое тесно связано с неевклидова геометрия многие математики и ученые сомневались, может ли обычное физическое пространство быть искривленным, хотя успех евклидовой геометрии до того времени означал, что радиус кривизны должен быть астрономически большим. В теории общая теория относительности, который описывает сила тяжести и космология, идея слегка обобщается на "кривизну пространство-время "; в теории относительности пространство-время псевдориманово многообразие. Как только временная координата определена, трехмерное пространство, соответствующее конкретному времени, обычно является искривленным римановым многообразием; но поскольку выбор временной координаты в значительной степени произвольный, физически значимым является искривление основного пространства-времени.
Хотя пространство произвольной кривизны очень сложно описать, кривизна пространства, которое локально изотропный и однородный описывается единственной гауссовой кривизной, как для поверхности; математически это сильные условия, но они соответствуют разумным физическим предположениям (все точки и все направления неразличимы). Положительная кривизна соответствует обратному квадрату радиуса кривизны; пример - сфера или гиперсфера. Пример отрицательно искривленного пространства: гиперболическая геометрия. Пространство или пространство-время с нулевой кривизной называется плоский. Например, Евклидово пространство является примером плоского пространства, а Пространство Минковского это пример плоского пространства-времени. Однако есть и другие примеры плоской геометрии в обеих настройках. А тор или цилиндр могут иметь плоские метрики, но различаются топология. Для искривленного пространства также возможны другие топологии. Смотрите также форма вселенной.
Обобщения

Математическое понятие кривизна также определяется в гораздо более общем контексте.[8] Многие из этих обобщений подчеркивают различные аспекты кривизны, как это понимается в более низких измерениях.
Одно из таких обобщений - кинематическое. Кривизну кривой, естественно, можно рассматривать как кинематическую величину, представляющую силу, которую испытывает определенный наблюдатель, движущийся по кривой; аналогично, кривизна в высших измерениях может рассматриваться как своего рода приливная сила (это один из способов мышления секционная кривизна ). Это обобщение кривизны зависит от того, как соседние пробные частицы расходятся или сходятся, когда им разрешено свободно перемещаться в пространстве; увидеть Поле Якоби.
Другое широкое обобщение кривизны связано с изучением параллельный транспорт на поверхности. Например, если вектор перемещается по петле на поверхности сферы, сохраняя параллельность на протяжении всего движения, то конечное положение вектора может не совпадать с исходным положением вектора. Это явление известно как голономия.[9] Различные обобщения в абстрактной форме фиксируют эту идею кривизны как меры голономии; увидеть форма кривизны. Близкое понятие кривизны происходит от калибровочная теория в физике, где кривизна представляет собой поле, а векторный потенциал поскольку поле - это величина, которая в целом зависит от пути: она может измениться, если наблюдатель перемещается по петле.
Еще два обобщения кривизны: скалярная кривизна и Кривизна Риччи. На изогнутой поверхности, такой как сфера, площадь диска на поверхности отличается от площади диска того же радиуса в плоском пространстве. Эта разница (в подходящем пределе) измеряется скалярной кривизной. Разница в площади сектора диска измеряется кривизной Риччи. Каждая из скалярной кривизны и кривизны Риччи определяется аналогичным образом в трех и более измерениях. Они особенно важны в теории относительности, где оба выступают на стороне Полевые уравнения Эйнштейна который представляет собой геометрию пространства-времени (другая сторона которого представляет присутствие материи и энергии). Эти обобщения кривизны лежат в основе, например, представления о том, что кривизна может быть свойством мера; увидеть кривизна меры.
Другое обобщение кривизны основано на способности сравнить искривленное пространство с другим пространством, в котором постоянный кривизна. Часто это делается с помощью треугольников в пробелах. Понятие треугольника имеет смысл в метрические пространства, и это приводит к КОТ(k) пробелы.
Смотрите также
- Форма кривизны для соответствующего понятия кривизны для векторные пучки и основные связки с участием связь
- Кривизна меры для понятия кривизны в теория меры
- Кривизна параметрических поверхностей
- Кривизна римановых многообразий для обобщений кривизны Гаусса на многомерные Римановы многообразия
- Вектор кривизны и геодезическая кривизна для соответствующих представлений о кривизне кривые в Римановы многообразия любой размерности
- Степень кривизны
- Дифференциальная геометрия кривых для полного рассмотрения кривых, вложенных в евклидово пространство произвольной размерности
- Диоптр, измерение кривизны, используемое в оптике
- Эволют, геометрическое место центров кривизны данной кривой
- Теорема Гаусса – Бонне для элементарного приложения кривизны
- Карта Гаусса для получения дополнительных геометрических свойств кривизны Гаусса
- Принцип наименьшего принуждения Гаусса, выражение Принцип наименьшего действия
- Средняя кривизна в одной точке на поверхности
- Минимальный радиус поворота железной дороги
- Радиус кривизны
- Вторая фундаментальная форма для внешней кривизны гиперповерхностей вообще
- Извилистость
- Кручение кривой
Заметки
эта статья не хватает ISBN для книг, перечисленных в нем. (Август 2017 г.) |
- ^ Клагетт, Маршалл (1968), Николь Орем и средневековая геометрия качеств и движений; трактат о единообразии и различии интенсивностей, известный как Tractatus de configurationibus qualitatum et motuum, Мэдисон: Univ. из Wisconsin Press, ISBN 0-299-04880-2
- ^ Серрано, Изабель; Сучава, Богдан (2015). "Средневековая тайна: концепция Николь Орем Curvitas" (PDF). Уведомления Американского математического общества. 62 (9): 1030–1034.
- ^ Боровик Александр; Кац, Михаил Г. (2011), «Кто дал вам сказку Коши – Вейерштрасса? Двойственная история строгого исчисления», Основы науки, 17 (3): 245–276, arXiv:1108.2885, Bibcode:2011arXiv1108.2885B, Дои:10.1007 / s10699-011-9235-х
- ^ Прессли, Эндрю. Элементарная дифференциальная геометрия (1-е изд.). п. 29.
- ^ Клайн, Моррис. Исчисление: интуитивный и физический подход (2-е изд.). п. 458.
- ^ Кеннеди, Джон (2011). «Параметризация кривой по длине дуги».
- ^ Гольдман, Р. (2005). «Формулы кривизны неявных кривых и поверхностей». Компьютерный геометрический дизайн. 22 (7): 632–658. CiteSeerX 10.1.1.413.3008. Дои:10.1016 / j.cagd.2005.06.005.
- ^ Кобаяши, С.; Номидзу, К. Основы дифференциальной геометрии. Wiley Interscience. т. 1 ч. 2–3.
- ^ Хендерсон; Таймина. Изучение геометрии (3-е изд.). С. 98–99.
использованная литература
- Кулидж, Дж. Л. (июнь 1952 г.). «Неудовлетворительная история кривизны». Американский математический ежемесячный журнал. 59 (6): 375–379. Дои:10.2307/2306807. JSTOR 2306807.
- Соколов, Д. Д. (2001) [1994], «Кривизна», Энциклопедия математики, EMS Press
- Клайн, Моррис (1998). Исчисление: интуитивный и физический подход. Дувр. С. 457–461. ISBN 978-0-486-40453-0. (ограниченная онлайн-копия, п. 457, в Google Книги )
- Клаф, А. Альберт (1956). Refresher по исчислению. Дувр. стр.151–168. ISBN 978-0-486-20370-6. (ограниченная онлайн-копия, п. 151, в Google Книги )
- Кейси, Джеймс (1996). Изучение кривизны. Vieweg + Teubner. ISBN 978-3-528-06475-4.












































