Собственные значения и собственные векторы - Eigenvalues and eigenvectors

В линейная алгебра, собственный вектор (/ˈаɪɡəпˌvɛkтər/) или же характеристический вектор из линейное преобразование ненулевой вектор это меняется на скаляр коэффициент, когда к нему применяется это линейное преобразование. Соответствующие собственное значение, часто обозначаемый ${ displaystyle lambda}$,^[1] - коэффициент масштабирования собственного вектора.

Геометрически, собственный вектор, соответствующий настоящий ненулевое собственное значение, указывает в направлении, в котором оно растянутый преобразованием, а собственное значение - коэффициент, на который он растягивается. Если собственное значение отрицательное, направление меняется на противоположное.^[2] Грубо говоря, в многомерном векторное пространство, собственный вектор не поворачивается.

Формальное определение

Если Т является линейным преобразованием из векторного пространства V через поле F в себя и v это ненулевой вектор в V, тогда v является собственным вектором Т если Т(v) является скалярным кратным v. Это можно записать как

${ Displaystyle Т ( mathbf {v}) = lambda mathbf {v},}$

куда λ является скаляром в F, известный как собственное значение, характеристическое значение, или же характерный корень связана с v.

Существует прямая переписка между п-к-п квадратные матрицы и линейные преобразования из п-размерный векторное пространство в себя при любом основа векторного пространства. Следовательно, в конечномерном векторном пространстве это эквивалентно определять собственные значения и собственные векторы, используя любой язык матрицы, или язык линейных преобразований.^[3][4]

Если V конечномерно, приведенное выше уравнение эквивалентно^[5]

${ displaystyle A mathbf {u} = lambda mathbf {u}.}$

куда А является матричным представлением Т и ты - координатный вектор v.

Обзор

Собственные значения и собственные векторы занимают важное место при анализе линейных преобразований. Префикс собственный- взят из Немецкий слово собственный (соотносится с английский слово собственный ) для «собственного», «характерного», «собственного».^[6][7] Первоначально использовался для учебы главные оси вращательного движения твердые тела, собственные значения и собственные векторы имеют широкий спектр приложений, например, в анализ устойчивости, анализ вибрации, атомные орбитали, распознавание лиц, и диагонализация матрицы.

По сути, собственный вектор v линейного преобразования Т - ненулевой вектор, который при Т наносится на него, не меняет направления. Применение Т к собственному вектору масштабирует только собственный вектор на скалярное значение λ, называемое собственным значением. Это условие можно записать в виде уравнения

${ Displaystyle Т ( mathbf {v}) = lambda mathbf {v},}$

называется уравнение на собственные значения или же собственное уравнение. В целом, λ может быть любой скаляр. Например, λ может быть отрицательным, и в этом случае собственный вектор меняет направление на противоположное как часть масштабирования, или он может быть нулевым или сложный.

В этом картирование сдвига красная стрелка меняет направление, а синяя - нет. Синяя стрелка является собственным вектором этого отображения сдвига, потому что он не меняет направления, а поскольку его длина не изменяется, его собственное значение равно 1.

В Мона Лиза Пример, изображенный здесь, представляет собой простую иллюстрацию. Каждую точку на картине можно представить как вектор, указывающий от центра картины к этой точке. Линейное преобразование в этом примере называется картирование сдвига. Точки в верхней половине перемещаются вправо, а точки в нижней половине - влево, пропорционально тому, насколько они удалены от горизонтальной оси, проходящей через середину рисунка. Поэтому векторы, указывающие на каждую точку исходного изображения, наклоняются вправо или влево, а в результате преобразования становятся длиннее или короче. Точки вдоль горизонтальная ось вообще не перемещается при применении этого преобразования. Следовательно, любой вектор, который указывает прямо вправо или влево без вертикального компонента, является собственным вектором этого преобразования, поскольку отображение не меняет своего направления. Более того, все эти собственные векторы имеют собственное значение, равное единице, потому что отображение также не меняет их длину.

Линейные преобразования могут принимать множество различных форм, отображая векторы в различных векторных пространствах, поэтому собственные векторы также могут принимать разные формы. Например, линейное преобразование может быть дифференциальный оператор подобно ${ displaystyle { tfrac {d} {dx}}}$, в этом случае собственные векторы являются функциями, называемыми собственные функции которые масштабируются этим дифференциальным оператором, например

${ displaystyle { frac {d} {dx}} e ^ { lambda x} = lambda e ^ { lambda x}.}$

В качестве альтернативы линейное преобразование может иметь форму п к п матрица, и в этом случае собственные векторы п на 1 матрицу. Если линейное преобразование выразить в виде п к п матрица А, то уравнение на собственные значения для линейного преобразования выше может быть переписано как матричное умножение

${ displaystyle Av = lambda v,}$

где собственный вектор v является п на 1 матрицу. Для матрицы собственные значения и собственные векторы могут использоваться для разложить матрицу - например, диагонализация Это.

Собственные значения и собственные векторы порождают множество тесно связанных математических понятий, и префикс собственный- широко применяется при их именовании:

• Набор всех собственных векторов линейного преобразования, каждый из которых спарен со своим соответствующим собственным значением, называется собственная система этой трансформации.^[8][9]
• Множество всех собственных векторов Т соответствующая одному и тому же собственному значению вместе с нулевым вектором называется собственное подпространство, или характерное пространство из Т связанное с этим собственным значением.^[10]
• Если набор собственных векторов Т образует основа области Т, то этот базис называется собственный базис.

История

Собственные значения часто вводятся в контексте линейная алгебра или же матричная теория. Однако исторически они возникли при изучении квадратичные формы и дифференциальные уравнения.

В 18 веке Леонард Эйлер изучал вращательное движение жесткое тело, и обнаружил важность главные оси.^[а] Жозеф-Луи Лагранж понял, что главные оси - это собственные векторы матрицы инерции.^[11]

В начале 19 века Огюстен-Луи Коши увидел, как их работу можно использовать для классификации квадратичные поверхности, и обобщил его до произвольных размеров.^[12] Коши также ввел термин racine caractéristique (характерный корень), для того, что сейчас называется собственное значение; его срок выживает в характеристическое уравнение.^[b]

Потом, Жозеф Фурье использовал работы Лагранжа и Пьер-Симон Лаплас решить уравнение теплопроводности к разделение переменных в его знаменитой книге 1822 года Теория аналитик де ля шалёр.^[13] Шарль-Франсуа Штурм развил идеи Фурье и привлек к ним внимание Коши, который объединил их со своими собственными идеями и пришел к тому факту, что реальные симметричные матрицы имеют действительные собственные значения.^[12] Это было продлено Чарльз Эрмит в 1855 г. до того, что сейчас называется Эрмитовы матрицы.^[14]

Примерно в то же время Франческо Бриоски доказал, что собственные значения ортогональные матрицы лежать на единичный круг,^[12] и Альфред Клебш нашел соответствующий результат для кососимметричные матрицы.^[14] Ну наконец то, Карл Вейерштрасс прояснил важный аспект в теория устойчивости начал Лаплас, осознав, что дефектные матрицы может вызвать нестабильность.^[12]

В это время, Джозеф Лиувиль изучал проблемы собственных значений, аналогичные задачам Штурма; дисциплина, выросшая из их работы, теперь называется Теория Штурма – Лиувилля.^[15] Шварц изучил первое собственное значение Уравнение Лапласа на общих владениях ближе к концу 19 века, а Пуанкаре учился Уравнение Пуассона несколькими годами позже.^[16]

В начале 20 века Дэвид Гильберт изучил собственные значения интегральные операторы рассматривая операторы как бесконечные матрицы.^[17] Он был первым, кто использовал Немецкий слово собственный, что означает "собственный",^[7] для обозначения собственных значений и собственных векторов в 1904 году,^[c] хотя он, возможно, следил за подобным использованием Герман фон Гельмгольц. Некоторое время стандартным термином на английском языке было «собственное значение», но сегодня стандартом является более характерный термин «собственное значение».^[18]

Первый численный алгоритм вычисления собственных значений и собственных векторов появился в 1929 году, когда Рихард фон Мизес опубликовал силовой метод. Один из самых популярных сегодня методов - QR-алгоритм, был предложен независимо Джон Г. Фрэнсис^[19] и Вера Кублановская^[20] в 1961 г.^[21][22]

Собственные значения и собственные векторы матриц

Собственные значения и собственные векторы часто знакомятся со студентами в контексте курсов линейной алгебры, посвященных матрицам.^[23][24]Кроме того, линейные преобразования в конечномерном векторном пространстве могут быть представлены с помощью матриц,^[25][4] что особенно часто встречается в численных и вычислительных приложениях.^[26]

Матрица А действует, растягивая вектор Икс, не меняя своего направления, поэтому Икс является собственным вектором А.

Учитывать п-мерные векторы, которые формируются в виде списка п скаляры, такие как трехмерные векторы

${ displaystyle x = { begin {bmatrix} 1 3 4 end {bmatrix}} quad { mbox {and}} quad y = { begin {bmatrix} -20 - 60 -80 end {bmatrix}}.}$

Эти векторы называются скалярные кратные друг друга, или параллельно или же коллинеарен, если есть скаляр λ такой, что

${ displaystyle x = lambda y.}$

В этом случае ${ displaystyle lambda = -1 / 20}$.

Теперь рассмотрим линейное преобразование п-мерные векторы, определяемые п к п матрица А,

${ Displaystyle Av = ш,}$

или же

${ displaystyle { begin {bmatrix} A_ {11} & A_ {12} & ldots & A_ {1n} A_ {21} & A_ {22} & ldots & A_ {2n} vdots & vdots & ddots & vdots A_ {n1} & A_ {n2} & ldots & A_ {nn} end {bmatrix}} { begin {bmatrix} v_ {1} v_ {2} vdots v_ {n} end {bmatrix}} = { begin {bmatrix} w_ {1} w_ {2} vdots w_ {n} end {bmatrix}}}$

где для каждой строки

${ displaystyle w_ {i} = A_ {i1} v_ {1} + A_ {i2} v_ {2} + cdots + A_ {in} v_ {n} = sum _ {j = 1} ^ {n} A_ {ij} v_ {j}}$.

Если это произойдет, v и ш являются скалярными кратными, то есть если

${ displaystyle Av = w = lambda v,}$

(1)

тогда v является собственный вектор линейного преобразования А и масштабный коэффициент λ это собственное значение соответствующий этому собственному вектору. Уравнение (1) это уравнение на собственные значения для матрицы А.

Уравнение (1) можно эквивалентно сформулировать как

${ displaystyle (A- lambda I) v = 0,}$

(2)

куда я это п к п единичная матрица а 0 - нулевой вектор.

Собственные значения и характеристический многочлен

Уравнение (2) имеет ненулевое решение v если и только если в детерминант матрицы (А − λI) равно нулю. Следовательно, собственные значения А ценности λ которые удовлетворяют уравнению

${ displaystyle | A- lambda I | = 0}$

(3)

С помощью Правило Лейбница для определителя левая часть уравнения (3) это многочлен функция переменной λ и степень этого полинома п, порядок матрицы А. Его коэффициенты зависят от записей А, за исключением того, что срок его степени п всегда (−1)^пλ^п. Этот многочлен называется характеристический многочлен из А. Уравнение (3) называется характеристическое уравнение или светское уравнение из А.

В основная теорема алгебры следует, что характеристический многочлен п-к-п матрица А, будучи полиномом степени п, возможно учтенный в продукт п линейные члены,

${ displaystyle | A- lambda I | = ( lambda _ {1} - lambda) ( lambda _ {2} - lambda) cdots ( lambda _ {n} - lambda),}$

(4)

где каждый λ_я может быть реальным, но в целом это комплексное число. Цифры λ₁, λ₂, ... λ_п, которые могут не иметь различных значений, являются корнями многочлена и собственными значениями А.

В качестве краткого примера, который более подробно описан в разделе примеров ниже, рассмотрим матрицу

${ displaystyle A = { begin {bmatrix} 2 & 1 1 & 2 end {bmatrix}}.}$

Принимая определитель (А − λI), характеристический многочлен А является

${ displaystyle | A- lambda I | = { begin {vmatrix} 2- lambda & 1 1 & 2- lambda end {vmatrix}} = 3-4 lambda + lambda ^ {2}.}$

Если положить характеристический полином равным нулю, он будет иметь корни в λ = 1 и λ = 3, которые являются двумя собственными значениями А. Собственные векторы, соответствующие каждому собственному значению, могут быть найдены путем решения для компонентов v в уравнении ${ displaystyle (A- lambda I) v = 0}$. В этом примере собственные векторы представляют собой любые ненулевые скалярные числа, кратные

${ displaystyle v _ { lambda = 1} = { begin {bmatrix} 1 - 1 end {bmatrix}}, quad v _ { lambda = 3} = { begin {bmatrix} 1 1 конец {bmatrix}}.}$

Если элементы матрицы А все являются действительными числами, то коэффициенты характеристического полинома также будут действительными числами, но собственные значения могут по-прежнему иметь ненулевые мнимые части. Поэтому элементы соответствующих собственных векторов также могут иметь ненулевые мнимые части. Точно так же собственные значения могут быть иррациональные числа даже если все записи А находятся рациональное число или даже если все они целые. Однако если записи А все алгебраические числа, которые включают рациональные числа, собственные значения - комплексные алгебраические числа.

Неверные корни действительного многочлена с действительными коэффициентами можно сгруппировать в пары комплексные конъюгаты, а именно с двумя членами каждой пары, имеющими мнимые части, которые отличаются только знаком, и одинаковую действительную часть. Если степень нечетная, то по теорема о промежуточном значении по крайней мере, один из корней настоящий. Поэтому любой вещественная матрица с нечетным порядком имеет по крайней мере одно действительное собственное значение, тогда как вещественная матрица с четным порядком может не иметь никаких действительных собственных значений. Собственные векторы, связанные с этими комплексными собственными значениями, также являются комплексными и также входят в комплексно сопряженные пары.

Алгебраическая множественность

Позволять λ_я быть собственным значением п к п матрица А. В алгебраическая кратность μ_А(λ_я) собственного значения является его множественность как корень характеристического полинома, т. е. наибольшего целого числа k такой, что (λ − λ_я)^k делится равномерно этот многочлен.^[10][27][28]

Предположим матрицу А имеет размер п и d ≤ п различные собственные значения. Принимая во внимание, что уравнение (4) множит характеристический многочлен А в продукт п линейные члены с потенциально повторяющимися членами, характеристический многочлен может быть записан как произведение d члены, каждый из которых соответствует отдельному собственному значению и возведен в степень алгебраической кратности,

${ displaystyle | A- lambda I | = ( lambda _ {1} - lambda) ^ { mu _ {A} ( lambda _ {1})} ( lambda _ {2} - lambda) ^ { mu _ {A} ( lambda _ {2})} cdots ( lambda _ {d} - lambda) ^ { mu _ {A} ( lambda _ {d})}.}.}$

Если d = п то правая часть - произведение п линейные члены, и это то же самое, что и Уравнение (4). Размер алгебраической кратности каждого собственного значения связан с размерностью п в качестве

${ Displaystyle { begin {align} 1 & leq mu _ {A} ( lambda _ {i}) leq n, mu _ {A} & = sum _ {i = 1} ^ { d} mu _ {A} left ( lambda _ {i} right) = n. end {align}}}$

Если μ_А(λ_я) = 1, то λ_я считается простое собственное значение.^[28] Если μ_А(λ_я) равна геометрической кратности λ_я, γ_А(λ_я), определенный в следующем разделе, то λ_я считается полупростое собственное значение.

Собственные подпространства, геометрическая кратность и собственный базис матриц

Учитывая конкретное собственное значение λ из п к п матрица Аопределить набор E быть всеми векторами v которые удовлетворяют уравнению (2),

${ displaystyle E = left { mathbf {v}: (A- lambda I) mathbf {v} = 0 right }.}$

С одной стороны, этот набор и есть ядро или пустое пространство матрицы (А − λI). С другой стороны, по определению, любой ненулевой вектор, удовлетворяющий этому условию, является собственным вектором А связана с λ. Итак, набор E это союз нулевого вектора с множеством всех собственных векторов А связана с λ, и E равно нулевому пространству (А − λI). E называется собственное подпространство или же характерное пространство из А связана с λ.^[29][10] В целом λ - комплексное число, а собственные векторы - комплексные п на 1 матрицу. Свойство нулевого пространства состоит в том, что это линейное подпространство, так E является линейным подпространством в ℂ^п.

Потому что собственное подпространство E - линейное подпространство, это закрыто под дополнением. То есть, если два вектора ты и v принадлежат к множеству E, написано ты, v ∈ E, тогда (ты + v) ∈ E или эквивалентно А(ты + v) = λ(ты + v). Это можно проверить с помощью распределительное свойство матричного умножения. Точно так же, потому что E - линейное подпространство, замкнутое относительно скалярного умножения. То есть, если v ∈ E а α - комплексное число, (αv) ∈ E или эквивалентно А(αv) = λ(αv). Это можно проверить, отметив, что умножение комплексных матриц на комплексные числа коммутативный. Так долго как ты + v и αv не равны нулю, они также являются собственными векторами А связана с λ.

Размерность собственного подпространства E связана с λ, или, что то же самое, максимальное количество линейно независимых собственных векторов, связанных с λ, называется собственным значением геометрическая кратность γ_А(λ). Потому что E также является нулевым пространством (А − λI) геометрическая кратность λ - размерность нулевого пространства (А − λI), также называемый ничтожность из (А − λI), который относится к размерности и рангу (А − λI) в качестве

${ displaystyle gamma _ {A} ( lambda) = n- operatorname {rank} (A- lambda I).}$

Из-за определения собственных значений и собственных векторов геометрическая кратность собственного значения должна быть не менее единицы, то есть каждое собственное значение имеет по крайней мере один связанный собственный вектор. Кроме того, геометрическая кратность собственного значения не может превышать его алгебраическую кратность. Кроме того, напомним, что алгебраическая кратность собственного значения не может превышать п.

${ Displaystyle 1 Leq гамма _ {A} ( lambda) leq mu _ {A} ( lambda) leq n}$

Чтобы доказать неравенство ${ displaystyle gamma _ {A} ( lambda) leq mu _ {A} ( lambda)}$рассмотрим, как из определения геометрической кратности следует существование ${ displaystyle gamma _ {A} ( lambda)}$ ортонормированные собственные векторы ${ displaystyle { boldsymbol {v}} _ {1}, , ldots, , { boldsymbol {v}} _ { gamma _ {A} ( lambda)}}$, так что ${ displaystyle A { boldsymbol {v}} _ {k} = lambda { boldsymbol {v}} _ {k}}$. Таким образом, мы можем найти (унитарную) матрицу ${ displaystyle V}$ чей первый ${ displaystyle gamma _ {A} ( lambda)}$ столбцы являются этими собственными векторами, а оставшиеся столбцы могут быть любым ортонормированным набором ${ Displaystyle п- гамма _ {A} ( лямбда)}$ векторы, ортогональные этим собственным векторам ${ displaystyle A}$. потом ${ displaystyle V}$ имеет полный ранг и, следовательно, обратим, и ${ displaystyle AV = VD}$ с ${ displaystyle D}$ матрица, верхний левый блок которой является диагональной матрицей ${ displaystyle lambda I _ { gamma _ {A} ( lambda)}}$. Отсюда следует, что ${ Displaystyle (A- xi I) V = V (D- xi I)}$. Другими словами, ${ Displaystyle A- xi I}$ похоже на ${ Displaystyle D- xi I}$, откуда следует, что ${ Displaystyle Det (A- xi I) = Det (D- xi I)}$. Но из определения ${ displaystyle D}$ мы знаем это ${ Displaystyle Det (D- xi I)}$ содержит фактор ${ Displaystyle ( хи - лямбда) ^ { гамма _ {А} ( лямбда)}}$, что означает, что алгебраическая кратность ${ displaystyle lambda}$ должен удовлетворить ${ displaystyle mu _ {A} ( lambda) geq gamma _ {A} ( lambda)}$.

Предполагать ${ displaystyle A}$ имеет ${ displaystyle d leq n}$ различные собственные значения ${ displaystyle lambda _ {1}, ..., lambda _ {d}}$, где геометрическая кратность ${ displaystyle lambda _ {i}}$ является ${ Displaystyle gamma _ {A} ( lambda _ {я})}$. Общая геометрическая кратность ${ displaystyle A}$,

${ displaystyle { begin {align} gamma _ {A} & = sum _ {i = 1} ^ {d} gamma _ {A} ( lambda _ {i}), d & leq гамма _ {A} leq n, end {выровнено}}}$

это размер сумма всех собственных подпространств ${ displaystyle A}$собственных значений, или, что то же самое, максимальное количество линейно независимых собственных векторов ${ displaystyle A}$. Если ${ displaystyle gamma _ {A} = n}$, тогда

• Прямая сумма собственных подпространств всех ${ displaystyle A}$собственные значения - это все векторное пространство ${ displaystyle mathbb {C} ^ {n}}$.
• Основа ${ displaystyle mathbb {C} ^ {n}}$ может быть сформирован из ${ displaystyle n}$ линейно независимые собственные векторы ${ displaystyle A}$; такая основа называется собственный базис
• Любой вектор в ${ displaystyle mathbb {C} ^ {n}}$ можно записать как линейную комбинацию собственных векторов ${ displaystyle A}$.

Дополнительные свойства собственных значений

Позволять ${ displaystyle A}$ быть произвольным ${ Displaystyle п раз п}$ матрица комплексных чисел с собственными значениями ${ displaystyle lambda _ {1}, ..., lambda _ {n}}$. Каждое собственное значение появляется ${ displaystyle mu _ {A} ( lambda _ {я})}$ раз в этом списке, где ${ displaystyle mu _ {A} ( lambda _ {я})}$ - алгебраическая кратность собственного значения. Ниже приведены свойства этой матрицы и ее собственных значений:

• В след из ${ displaystyle A}$, определяемая как сумма его диагональных элементов, также является суммой всех собственных значений,

  ${ displaystyle operatorname {tr} (A) = sum _ {i = 1} ^ {n} a_ {ii} = sum _ {i = 1} ^ {n} lambda _ {i} = lambda _ {1} + lambda _ {2} + cdots + lambda _ {n}.}$^[30][31][32]

• В детерминант из ${ displaystyle A}$ является произведением всех собственных значений,

  ${ displaystyle det (A) = prod _ {i = 1} ^ {n} lambda _ {i} = lambda _ {1} lambda _ {2} cdots lambda _ {n}.}$^[30][33][34]

• Собственные значения ${ displaystyle k}$^th сила ${ displaystyle A}$; т.е. собственные значения ${ displaystyle A ^ {k}}$, для любого положительного целого числа ${ displaystyle k}$, находятся ${ displaystyle lambda _ {1} ^ {k}, ..., lambda _ {n} ^ {k}}$.
• Матрица ${ displaystyle A}$ является обратимый тогда и только тогда, когда каждое собственное значение ненулевое.
• Если ${ displaystyle A}$ обратима, то собственные значения ${ displaystyle A ^ {- 1}}$ находятся ${ displaystyle { frac {1} { lambda _ {1}}}, ..., { frac {1} { lambda _ {n}}}}$ и геометрическая кратность каждого собственного значения совпадает. Более того, поскольку характеристический многочлен обратного обратный многочлен оригинала собственные значения имеют одинаковую алгебраическую кратность.
• Если ${ displaystyle A}$ равен своему сопряженный транспонировать ${ displaystyle A ^ {*}}$, или эквивалентно, если ${ displaystyle A}$ является Эрмитский, то каждое собственное значение вещественно. То же самое и с любым симметричный вещественная матрица.
• Если ${ displaystyle A}$ не только эрмитский, но и положительно определенный, положительно-полуопределенный, отрицательно-определенный или отрицательно-полуопределенный, то каждое собственное значение будет положительным, неотрицательным, отрицательным или неположительным соответственно.
• Если ${ displaystyle A}$ является унитарный, каждое собственное значение имеет модуль ${ Displaystyle | лямбда _ {я} | = 1}$.
• если ${ displaystyle A}$ это ${ Displaystyle п раз п}$ матрица и ${ displaystyle { lambda _ {1}, ldots, lambda _ {k} }}$ являются ее собственными значениями, то собственные значения матрицы ${ displaystyle I + A}$ (куда ${ displaystyle I}$ - единичная матрица) являются ${ displaystyle { lambda _ {1} +1, ldots, lambda _ {k} +1 }}$. Более того, если ${ Displaystyle альфа в mathbb {C}}$, собственные значения ${ displaystyle alpha I + A}$ находятся ${ displaystyle { lambda _ {1} + alpha, ldots, lambda _ {k} + alpha }}$. В более общем смысле, для полинома ${ displaystyle P}$ собственные значения матрицы ${ Displaystyle P (A)}$ находятся ${ Displaystyle {P ( lambda _ {1}), ldots, P ( lambda _ {k}) }}$.

Левый и правый собственные векторы

Многие дисциплины традиционно представляют векторы как матрицы с одним столбцом, а не как матрицы с одной строкой. По этой причине слово «собственный вектор» в контексте матриц почти всегда относится к правый собственный вектор, а именно столбец вектор, который верно умножает ${ Displaystyle п раз п}$ матрица ${ displaystyle A}$ в определяющем уравнении Уравнение (1),

${ displaystyle Av = lambda v.}$

Задача на собственные значения и собственные векторы также может быть определена для ряд векторы, которые оставили матрица умножения ${ displaystyle A}$. В этой формулировке определяющим уравнением является

${ Displaystyle иА = каппа и,}$

куда ${ displaystyle kappa}$ скаляр и ${ displaystyle u}$ это ${ Displaystyle 1 раз п}$ матрица. Любой вектор-строка ${ displaystyle u}$ удовлетворяющий этому уравнению, называется левый собственный вектор из ${ displaystyle A}$ и ${ displaystyle kappa}$ ассоциированное с ним собственное значение. Транспонируя это уравнение,

${ displaystyle A ^ { extf {T}} u ^ { extf {T}} = kappa u ^ { extf {T}}.}$

Сравнивая это уравнение с уравнением (1), сразу следует, что левый собственный вектор ${ displaystyle A}$ то же самое, что транспонирование правого собственного вектора ${ Displaystyle А ^ { extf {T}}}$, с тем же собственным значением. Кроме того, поскольку характеристический многочлен ${ Displaystyle А ^ { extf {T}}}$ совпадает с характеристическим полиномом ${ displaystyle A}$, собственные значения левых собственных векторов ${ displaystyle A}$ такие же, как собственные значения правых собственных векторов ${ Displaystyle A ^ { extf {T}}}$.

Диагонализация и собственное разложение

Предположим, что собственные векторы А составляют основу, или что то же самое А имеет п линейно независимые собственные векторы v₁, v₂, ..., v_п с соответствующими собственными значениями λ₁, λ₂, ..., λ_п. Собственные значения не обязательно должны быть разными. Определите квадратную матрицу Q чьи столбцы п линейно независимые собственные векторы А,

${ displaystyle Q = { begin {bmatrix} v_ {1} & v_ {2} & cdots & v_ {n} end {bmatrix}}.}$

Поскольку каждый столбец Q является собственным вектором А, умножение вправо А к Q масштабирует каждый столбец Q по собственному значению,

${ displaystyle AQ = { begin {bmatrix} lambda _ {1} v_ {1} & lambda _ {2} v_ {2} & cdots & lambda _ {n} v_ {n} end {bmatrix }}.}$

Имея это в виду, определим диагональную матрицу Λ, где каждый диагональный элемент Λ_ii - собственное значение, связанное с я-й столбец Q. потом

${ displaystyle AQ = Q Lambda.}$

Поскольку столбцы Q линейно независимы, Q обратима. Справа, умножив обе части уравнения на Q⁻¹,

${ displaystyle A = Q Lambda Q ^ {- 1},}$

или вместо этого умножая обе стороны слева на Q⁻¹,

${ displaystyle Q ^ {- 1} AQ = Lambda.}$

А поэтому может быть разложена на матрицу, состоящую из собственных векторов, диагональную матрицу с собственными значениями по диагонали и матрицу, обратную матрице собственных векторов. Это называется собственное разложение и это преобразование подобия. Такая матрица А как говорят похожий диагональной матрице Λ или диагонализуемый. Матрица Q - изменение базисной матрицы преобразования подобия. По сути, матрицы А и Λ представляют собой одно и то же линейное преобразование, выраженное в двух разных базах. Собственные векторы используются в качестве основы при представлении линейного преобразования как Λ.

Наоборот, предположим, что матрица А диагонализуема. Позволять п - невырожденная квадратная матрица такая, что п⁻¹AP это некоторая диагональная матрица D. Осталось умножить оба на п, AP = PD. Каждый столбец п поэтому должен быть собственным вектором А собственное значение которого является соответствующим диагональным элементом D. Поскольку столбцы п должен быть линейно независимым для п быть обратимым, существуют п линейно независимые собственные векторы А. Отсюда следует, что собственные векторы матрицы А составляют основу тогда и только тогда, когда А диагонализуема.

Матрица, которая не диагонализуема, называется дефектный. Для дефектных матриц понятие собственных векторов обобщается на обобщенные собственные векторы а диагональная матрица собственных значений обобщается на Нормальная форма Джордана. Над алгебраически замкнутым полем любая матрица А имеет Нормальная форма Джордана и поэтому допускает базис из обобщенных собственных векторов и разложение на обобщенные собственные подпространства.

Вариационная характеристика

в Эрмитский В этом случае собственным значениям можно дать вариационную характеристику. Наибольшее собственное значение ${ displaystyle H}$ это максимальное значение квадратичная форма ${ Displaystyle х ^ { extf {T}} Hx / x ^ { extf {T}} x}$. Ценность ${ displaystyle x}$ который реализует этот максимум, является собственным вектором.

Примеры матриц

Пример двумерной матрицы

Матрица преобразования А = ${ displaystyle { bigl [} { begin {smallmatrix} 2 & 1 1 & 2 end {smallmatrix}} { bigr]}}$ сохраняет направление фиолетовых векторов параллельно v_λ=1 = [1 −1]^Т и синие векторы, параллельные v_λ=3 = [1 1]^Т. Красные векторы не параллельны ни одному из собственных векторов, поэтому их направления изменяются преобразованием. Длины фиолетовых векторов не изменяются после преобразования (из-за их собственного значения 1), в то время как синие векторы в три раза больше длины оригинала (из-за их собственного значения 3). Смотрите также: Расширенная версия, показывающая все четыре квадранта.

Рассмотрим матрицу

${ displaystyle A = { begin {bmatrix} 2 & 1 1 & 2 end {bmatrix}}.}$

На рисунке справа показано влияние этого преобразования на координаты точки на плоскости. v этого преобразования удовлетворяют уравнению (1), а значения λ для которого определитель матрицы (А − λI) равны нулю - собственные значения.

Взяв определитель, чтобы найти характеристический многочлен А,

${ displaystyle { begin {align} | A- lambda I | & = left | { begin {bmatrix} 2 & 1 1 & 2 end {bmatrix}} - lambda { begin {bmatrix} 1 & 0 0 & 1 end {bmatrix}} right | = { begin {vmatrix} 2- lambda & 1 1 & 2- lambda end {vmatrix}}, [6pt] & = 3-4 lambda + lambda ^ {2}. End {выравнивается}}}$

Если положить характеристический полином равным нулю, он будет иметь корни в λ=1 и λ=3, которые являются двумя собственными значениями А.

За λ=1, Уравнение (2) становится,

${ Displaystyle (AI) v _ { lambda = 1} = { begin {bmatrix} 1 & 1 1 & 1 end {bmatrix}} { begin {bmatrix} v_ {1} v_ {2} end {bmatrix }} = { begin {bmatrix} 0 0 end {bmatrix}}}$

${ displaystyle 1v_ {1} + 1v_ {2} = 0}$; ${ displaystyle 1v_ {1} + 1v_ {2} = 0}$

Любой ненулевой вектор с v₁ = −v₂ решает это уравнение. Следовательно,

${ displaystyle v _ { lambda = 1} = { begin {bmatrix} v_ {1} - v_ {1} end {bmatrix}} = { begin {bmatrix} 1 - 1 end {bmatrix }}}$

является собственным вектором А соответствующий λ = 1, как и любое скалярное кратное этого вектора.

За λ=3, Уравнение (2) становится

${ displaystyle (A-3I) v _ { lambda = 3} = { begin {bmatrix} -1 & 1 1 & -1 end {bmatrix}} { begin {bmatrix} v_ {1} v_ {2 } end {bmatrix}} = { begin {bmatrix} 0 0 end {bmatrix}}}$

${ displaystyle -1v_ {1} + 1v_ {2} = 0}$; ${ displaystyle 1v_ {1} -1v_ {2} = 0}$

Любой ненулевой вектор с v₁ = v₂ решает это уравнение. Следовательно,

${ Displaystyle v _ { lambda = 3} = { begin {bmatrix} v_ {1} v_ {1} end {bmatrix}} = { begin {bmatrix} 1 1 end {bmatrix}} }$

является собственным вектором А соответствующий λ = 3, как и любое скалярное кратное этого вектора.

Таким образом, векторы v_λ=1 и v_λ=3 являются собственными векторами А связанные с собственными значениями λ=1 и λ=3, соответственно.

Пример трехмерной матрицы

Рассмотрим матрицу

${ displaystyle A = { begin {bmatrix} 2 & 0 & 0 0 & 3 & 4 0 & 4 & 9 end {bmatrix}}.}$

Характеристический многочлен А является

${ displaystyle { begin {align} | A- lambda I | & = left | { begin {bmatrix} 2 & 0 & 0 0 & 3 & 4 0 & 4 & 9 end {bmatrix}} - lambda { begin {bmatrix} 1 & 0 & 0 0 & 1 & 0 0 & 0 & 1 end {bmatrix}} right | = { begin {vmatrix} 2- lambda & 0 & 0 0 & 3- lambda & 4 0 & 4 & 9- lambda end {vmatrix}}, [ 6pt] & = (2- lambda) { bigl [} (3- lambda) (9- lambda) -16 { bigr]} = - lambda ^ {3} +14 lambda ^ {2} -35 лямбда +22. Конец {выровнено}}}$

Корни характеристического полинома равны 2, 1 и 11, которые являются единственными тремя собственными значениями А. Эти собственные значения соответствуют собственным векторам ${ displaystyle { begin {bmatrix} 1 & 0 & 0 end {bmatrix}} ^ { extf {T}},}$ ${ displaystyle { begin {bmatrix} 0 & -2 & 1 end {bmatrix}} ^ { extf {T}},}$ и ${ displaystyle { begin {bmatrix} 0 & 1 & 2 end {bmatrix}} ^ { extf {T}}}$, или любое ненулевое кратное ему.

Пример трехмерной матрицы с комплексными собственными значениями

Рассмотрим матрица циклической перестановки

${ displaystyle A = { begin {bmatrix} 0 & 1 & 0 0 & 0 & 1 1 & 0 & 0 end {bmatrix}}.}$

Эта матрица сдвигает координаты вектора вверх на одну позицию и перемещает первую координату вниз. Его характеристический полином равен 1 -λ³, чьи корни

${ displaystyle { begin {align} lambda _ {1} & = 1 lambda _ {2} & = - { frac {1} {2}} + mathbf {i} { frac { sqrt {3}} {2}} lambda _ {3} & = lambda _ {2} ^ {*} = - { frac {1} {2}} - mathbf {i} { frac { sqrt {3}} {2}} конец {выровнено}}}$

куда ${ Displaystyle mathbf {я}}$ мнимая единица с ${ displaystyle mathbf {i} ^ {2} = - 1.}$

Для действительного собственного значения λ₁ = 1, любой вектор с тремя равными ненулевыми элементами является собственным вектором. Например,

${ Displaystyle A { begin {bmatrix} 5 5 5 end {bmatrix}} = { begin {bmatrix} 5 5 5 end {bmatrix}} = 1 cdot { begin {bmatrix} 5 5 5 end {bmatrix}}.}$

Для комплексно сопряженной пары мнимых собственных значений

${ displaystyle lambda _ {2} lambda _ {3} = 1, quad lambda _ {2} ^ {2} = lambda _ {3}, quad lambda _ {3} ^ {2} = lambda _ {2}.}$

потом

${ displaystyle A { begin {bmatrix} 1 lambda _ {2} lambda _ {3} end {bmatrix}} = { begin {bmatrix} lambda _ {2} lambda _ {3} 1 end {bmatrix}} = lambda _ {2} cdot { begin {bmatrix} 1 lambda _ {2} lambda _ {3} end {bmatrix} },}$

и

${ displaystyle A { begin {bmatrix} 1 lambda _ {3} lambda _ {2} end {bmatrix}} = { begin {bmatrix} lambda _ {3} lambda _ {2} 1 end {bmatrix}} = lambda _ {3} cdot { begin {bmatrix} 1 lambda _ {3} lambda _ {2} end {bmatrix} }.}$

Следовательно, два других собственных вектора матрицы А сложные и ${ displaystyle v _ { lambda _ {2}} = { begin {bmatrix} 1 & lambda _ {2} & lambda _ {3} end {bmatrix}} ^ { extf {T}}}$ и ${ displaystyle v _ { lambda _ {3}} = { begin {bmatrix} 1 & lambda _ {3} & lambda _ {2} end {bmatrix}} ^ { extf {T}}}$ с собственными значениями λ₂ и λ₃, соответственно. Два комплексных собственных вектора также входят в комплексно сопряженную пару:

${ displaystyle v _ { lambda _ {2}} = v _ { lambda _ {3}} ^ {*}.}$

Пример диагональной матрицы

Матрицы с элементами только по главной диагонали называются диагональные матрицы. Собственные значения диагональной матрицы - это сами диагональные элементы. Рассмотрим матрицу

${ displaystyle A = { begin {bmatrix} 1 & 0 & 0 0 & 2 & 0 0 & 0 & 3 end {bmatrix}}.}$

Характеристический многочлен А является

${ Displaystyle | A- лямбда I | = (1- лямбда) (2- лямбда) (3- лямбда),}$

имеющий корни λ₁=1, λ₂=2, и λ₃=3. Эти корни являются диагональными элементами, а также собственными значениямиА.

Каждый диагональный элемент соответствует собственному вектору, единственный ненулевой компонент которого находится в той же строке, что и этот диагональный элемент. В этом примере собственные значения соответствуют собственным векторам,

${ displaystyle v _ { lambda _ {1}} = { begin {bmatrix} 1 0 0 end {bmatrix}}, quad v _ { lambda _ {2}} = { begin {bmatrix } 0 1 0 end {bmatrix}}, quad v _ { lambda _ {3}} = { begin {bmatrix} 0 0 1 end {bmatrix}},}$

соответственно, а также скалярные кратные этих векторов.

Пример треугольной матрицы

Матрица, у которой все элементы над главной диагональю равны нулю, называется ниже треугольная матрица, а матрица, все элементы которой ниже главной диагонали равны нулю, называется верхнетреугольная матрица. Как и в случае диагональных матриц, собственные значения треугольных матриц являются элементами главной диагонали.

Рассмотрим нижнюю треугольную матрицу,

${ displaystyle A = { begin {bmatrix} 1 & 0 & 0 1 & 2 & 0 2 & 3 & 3 end {bmatrix}}.}$

Характеристический многочлен А является

${ Displaystyle | A- лямбда I | = (1- лямбда) (2- лямбда) (3- лямбда),}$

имеющий корни λ₁=1, λ₂=2, и λ₃=3. Эти корни являются диагональными элементами, а также собственными значениямиА.

Эти собственные значения соответствуют собственным векторам,

${ displaystyle v _ { lambda _ {1}} = { begin {bmatrix} 1 - 1 { frac {1} {2}} end {bmatrix}}, quad v _ { lambda _ {2}} = { begin {bmatrix} 0 1 - 3 end {bmatrix}}, quad v _ { lambda _ {3}} = { begin {bmatrix} 0 0 1 end {bmatrix}},}$

соответственно, а также скалярные кратные этих векторов.

Пример матрицы с повторяющимися собственными значениями

Как и в предыдущем примере, нижняя треугольная матрица

${ displaystyle A = { begin {bmatrix} 2 & 0 & 0 & 0 1 & 2 & 0 & 0 0 & 1 & 3 & 0 0 & 0 & 1 & 3 end {bmatrix}},}$

имеет характеристический многочлен, который является произведением его диагональных элементов,

${ displaystyle | A- lambda I | = { begin {vmatrix} 2- lambda & 0 & 0 & 0 1 & 2- lambda & 0 & 0 0 & 1 & 3- lambda & 0 0 & 0 & 1 & 3- lambda end {vmatrix}} = ( 2- lambda) ^ {2} (3- lambda) ^ {2}.}$

Корни этого многочлена, а следовательно, и собственные значения, равны 2 и 3. алгебраическая кратность каждого собственного значения 2; другими словами, они оба являются двойными корнями. Сумма алгебраических кратностей всех различных собственных значений равна μ_А = 4 = п, порядок характеристического полинома и размерность А.

С другой стороны, геометрическая кратность собственного значения 2 составляет всего 1, потому что его собственное подпространство охватывает только один вектор ${ displaystyle { begin {bmatrix} 0 & 1 & -1 & 1 end {bmatrix}} ^ { extf {T}}}$ и поэтому одномерный. Точно так же геометрическая кратность собственного значения 3 равна 1, потому что его собственное подпространство натянуто только на один вектор ${ displaystyle { begin {bmatrix} 0 & 0 & 0 & 1 end {bmatrix}} ^ { extf {T}}}$. Общая геометрическая кратность γ_А равно 2, что является наименьшим значением для матрицы с двумя различными собственными значениями. Геометрические множественности определены в следующем разделе.

Тождество собственного вектора и собственного значения

Для Эрмитова матрица, квадрат нормы j-й компонент нормализованного собственного вектора может быть вычислен с использованием только собственных значений матрицы и собственных значений соответствующих малая матрица,

$${ displaystyle | v_ {i, j} | ^ {2} = { frac { prod _ {k} {( lambda _ {i} - lambda _ {k} (M_ {j}))}} { prod _ {k neq i} {( lambda _ {i} - lambda _ {k})}}},}$$

${ textstyle M_ {j}}$

Собственные значения и собственные функции дифференциальных операторов

Определения собственного значения и собственных векторов линейного преобразования Т остается в силе, даже если лежащее в основе векторное пространство является бесконечномерным Гильберта или же Банахово пространство. Широко используемым классом линейных преобразований, действующих на бесконечномерные пространства, являются дифференциальные операторы на функциональные пространства. Позволять D - линейный дифференциальный оператор в пространстве C^∞ бесконечно дифференцируемый реальные функции реального аргумента т. Уравнение на собственные значения для D это дифференциальное уравнение

${ Displaystyle Df (t) = лямбда f (t)}$

Функции, удовлетворяющие этому уравнению, являются собственными векторами D и обычно называются собственные функции.

Пример производного оператора

Рассмотрим производный оператор ${ displaystyle { tfrac {d} {dt}}}$ с уравнением на собственные значения

${ displaystyle { frac {d} {dt}} f (t) = lambda f (t).}$

Это дифференциальное уравнение можно решить, умножив обе части на dt/ж(т) и интегрируя. Его решение, экспоненциальная функция

${ Displaystyle е (т) = е (0) е ^ { лямбда т},}$

- собственная функция производного оператора.В этом случае собственная функция сама является функцией связанного с ней собственного значения. В частности, для λ = 0 собственная функция ж(т) - постоянная.

Главный собственная функция В статье приведены другие примеры.

Общее определение

Понятие собственных значений и собственных векторов естественным образом распространяется на произвольные линейные преобразования на произвольных векторных пространствах. Позволять V любое векторное пространство над некоторым поле K из скаляры, и разреши Т отображение линейного преобразования V в V,

${ displaystyle T: V to V.}$

Мы говорим, что ненулевой вектор v ∈ V является собственный вектор из Т тогда и только тогда, когда существует скаляр λ ∈ K такой, что

${ Displaystyle Т ( mathbf {v}) = lambda mathbf {v}.}$

(5)

Это уравнение называется уравнением на собственные значения для Т, а скаляр λ это собственное значение из Т соответствующий собственному вектору v. Т(v) является результатом применения преобразования Т к вектору v, пока λv это произведение скаляра λ с v.^[38][39]

Собственные подпространства, геометрическая кратность и собственный базис

Учитывая собственное значение λ, рассмотрим множество

${ displaystyle E = left { mathbf {v}: T ( mathbf {v}) = lambda mathbf {v} right },}$

который представляет собой объединение нулевого вектора с множеством всех собственных векторов, связанных сλ. E называется собственное подпространство или же характерное пространство из Т связана сλ.

По определению линейного преобразования

${ Displaystyle { begin {align} T ( mathbf {x} + mathbf {y}) & = T ( mathbf {x}) + T ( mathbf {y}), T ( alpha mathbf {x}) & = alpha T ( mathbf {x}), end {align}}}$

за (Икс,у) ∈ V и α ∈ K. Следовательно, если ты и v являются собственными векторами Т связанный с собственным значением λ, а именно ты,v ∈ E, тогда

${ Displaystyle { begin {align} T ( mathbf {u} + mathbf {v}) & = lambda ( mathbf {u} + mathbf {v}), T ( alpha mathbf { v}) & = lambda ( alpha mathbf {v}). end {выравнивается}}}$

Итак, оба ты + v и αv являются либо нулевыми, либо собственными векторами Т связана с λ, а именно ты + v, αv ∈ E, и E замкнуто относительно сложения и скалярного умножения. Собственное подпространство E связана с λ поэтому является линейным подпространством в V.^[40]Если это подпространство имеет размерность 1, его иногда называют собственная линия.^[41]

В геометрическая кратность γ_Т(λ) собственного значения λ размерность собственного подпространства, связанного с λ, то есть максимальное количество линейно независимых собственных векторов, связанных с этим собственным значением.^[10][28] По определению собственных значений и собственных векторов γ_Т(λ) ≥ 1, поскольку каждое собственное значение имеет хотя бы один собственный вектор.

Собственные подпространства Т всегда составлять прямая сумма. Как следствие, собственные векторы разные собственные значения всегда линейно независимы. Следовательно, сумма размеров собственных подпространств не может превышать размерности п векторного пространства, на котором Т действует, и не может быть больше, чем п различные собственные значения.^[d]

Любое подпространство, порожденное собственными векторами Т является инвариантное подпространство из Т, а ограничение Т в такое подпространство диагонализуемо. Более того, если все векторное пространство V можно натянуть на собственные векторы Т, или, что то же самое, если прямая сумма собственных подпространств, связанных со всеми собственными значениями Т это все векторное пространство V, то основа V называется собственный базис могут быть сформированы из линейно независимых собственных векторов Т. Когда Т допускает собственный базис, Т диагонализуема.

Нулевой вектор как собственный вектор

Хотя определение собственного вектора, используемое в этой статье, исключает нулевой вектор, можно определить собственные значения и собственные векторы так, чтобы нулевой вектор был собственным вектором.^[42]

Снова рассмотрим уравнение на собственные значения, Уравнение (5). Определить собственное значение быть любым скаляром λ ∈ K такой, что существует ненулевой вектор v ∈ V удовлетворяющее уравнению (5). Важно, чтобы в этой версии определения собственного значения указывается, что вектор не равен нулю, иначе по этому определению нулевой вектор допускает любой скаляр в K быть собственным значением. Определить собственный вектор v связанный с собственным значением λ быть любым вектором, который, учитывая λ, удовлетворяет уравнению (5). Учитывая собственное значение, нулевой вектор находится среди векторов, которые удовлетворяют уравнению (5), поэтому нулевой вектор включается в число собственных векторов этим альтернативным определением.

Спектральная теория

Если λ является собственным значением Т, то оператор (Т − λI) не взаимно однозначно, поэтому обратное (Т − λI)⁻¹ не существует. Обратное верно для конечномерных векторных пространств, но не для бесконечномерных векторных пространств. В общем, оператор (Т − λI) может не иметь обратного, даже если λ не является собственным значением.

По этой причине в функциональный анализ собственные значения могут быть обобщены на спектр линейного оператора Т как набор всех скаляров λ для которого оператор (Т − λI) не имеет ограниченный обратный. Спектр оператора всегда содержит все его собственные значения, но не ограничивается ими.

Ассоциативные алгебры и теория представлений

Можно обобщить алгебраический объект, действующий в векторном пространстве, заменив единственный оператор, действующий в векторном пространстве, на представление алгебры - ан ассоциативная алгебра действуя на модуль. Изучение таких действий - область теория представлений.

В теоретико-репрезентативное понятие веса является аналогом собственных значений, а весовые векторы и весовые пространства являются аналогами собственных векторов и собственных подпространств соответственно.

Динамические уравнения

Простейший разностные уравнения иметь форму

${ displaystyle x_ {t} = a_ {1} x_ {t-1} + a_ {2} x_ {t-2} + cdots + a_ {k} x_ {t-k}.}$

Решение этого уравнения для Икс с точки зрения т находится с помощью его характеристического уравнения

${ displaystyle lambda ^ {k} -a_ {1} lambda ^ {k-1} -a_ {2} lambda ^ {k-2} - cdots -a_ {k-1} lambda -a_ { k} = 0,}$

которые можно найти, сложив в матрицу систему уравнений, состоящую из приведенного выше разностного уравнения и k - 1 уравнение ${ Displaystyle х_ {т-1} = х_ {т-1}, точки, х_ {т-к + 1} = х_ {т-к + 1},}$ давая k-мерная система первого порядка в векторе суммированных переменных ${ displaystyle { begin {bmatrix} x_ {t} & cdots & x_ {t-k + 1} end {bmatrix}}}$ в терминах его однократно запаздывающего значения и взятия характеристического уравнения матрицы этой системы. Это уравнение дает k характерные корни ${ displaystyle lambda _ {1}, , ldots, , lambda _ {k},}$ для использования в решении уравнения

${ displaystyle x_ {t} = c_ {1} lambda _ {1} ^ {t} + cdots + c_ {k} lambda _ {k} ^ {t}.}$

Аналогичная процедура используется для решения дифференциальное уравнение формы

${ displaystyle { frac {d ^ {k} x} {dt ^ {k}}} + a_ {k-1} { frac {d ^ {k-1} x} {dt ^ {k-1} }} + cdots + a_ {1} { frac {dx} {dt}} + a_ {0} x = 0.}$

Расчет

Вычисление собственных значений и собственных векторов - это тема, в которой теория, представленная в учебниках элементарной линейной алгебры, часто очень далека от практики.

Классический метод

Классический метод состоит в том, чтобы сначала найти собственные значения, а затем вычислить собственные векторы для каждого собственного значения. Во многих отношениях он плохо подходит для неточной арифметики, такой как плавающая точка.

Собственные значения

Собственные значения матрицы ${ displaystyle A}$ можно определить, найдя корни характеристического многочлена. Это легко для ${ displaystyle 2 times 2}$ матрицы, но сложность быстро увеличивается с увеличением размера матрицы.

Теоретически коэффициенты характеристического полинома можно вычислить точно, поскольку они являются суммами произведений матричных элементов; и есть алгоритмы, которые могут найти все корни многочлена произвольной степени до любой требуемой точность.^[43] Однако на практике этот подход нежизнеспособен, поскольку коэффициенты будут загрязнены неизбежными ошибки округления, а корни полинома могут быть чрезвычайно чувствительной функцией коэффициентов (как показано на примере Полином Уилкинсона ).^[43] Даже для матриц, элементы которых являются целыми числами, вычисление становится нетривиальным, поскольку суммы очень велики; постоянный член - это детерминант, что для ${ Displaystyle п раз п}$ это сумма ${ displaystyle n!}$ разные продукты.^[e]

Явный алгебраические формулы так как корни многочлена существуют, только если степень ${ displaystyle n}$ 4 или меньше. Согласно Теорема Абеля – Руффини не существует общей, явной и точной алгебраической формулы для корней многочлена степени 5 или выше. (Общность имеет значение, потому что любой многочлен со степенью ${ displaystyle n}$ - характеристический многочлен некоторого сопутствующая матрица порядка ${ displaystyle n}$.) Следовательно, для матриц порядка 5 и более собственные значения и собственные векторы не могут быть получены с помощью явной алгебраической формулы и, следовательно, должны быть вычислены с помощью приближенного численные методы. Даже точная формула для корней многочлена степени 3 численно нецелесообразно.

Собственные векторы

Как только (точное) значение собственного значения известно, соответствующие собственные векторы могут быть найдены путем нахождения ненулевых решений уравнения для собственных значений, которое становится система линейных уравнений с известными коэффициентами. Например, если известно, что 6 - собственное значение матрицы

${ displaystyle A = { begin {bmatrix} 4 & 1 6 & 3 end {bmatrix}}}$

мы можем найти его собственные векторы, решив уравнение ${ displaystyle Av = 6v}$, то есть

${ displaystyle { begin {bmatrix} 4 & 1 6 & 3 end {bmatrix}} { begin {bmatrix} x y end {bmatrix}} = 6 cdot { begin {bmatrix} x y конец {bmatrix}}}$

Это матричное уравнение эквивалентно двум линейные уравнения

${ displaystyle left {{ begin {align} 4x + y & = 6x 6x + 3y & = 6y end {align}} right.}$      то есть      ${ displaystyle left {{ begin {align} -2x + y & = 0 6x-3y & = 0 end {align}} right.}$

Оба уравнения сводятся к одному линейному уравнению ${ displaystyle y = 2x}$. Следовательно, любой вектор вида ${ displaystyle { begin {bmatrix} a 2a end {bmatrix}}}$, для любого ненулевого действительного числа ${ displaystyle a}$, является собственным вектором ${ displaystyle A}$ с собственным значением ${ displaystyle lambda = 6}$.

Матрица ${ displaystyle A}$ выше имеет другое собственное значение ${ displaystyle lambda = 1}$. Аналогичный расчет показывает, что соответствующие собственные векторы являются ненулевыми решениями ${ displaystyle 3x + y = 0}$, то есть любой вектор вида ${ displaystyle { begin {bmatrix} b - 3b end {bmatrix}}}$, для любого ненулевого действительного числа ${ displaystyle b}$.

Простые итерационные методы

Обратный подход, когда сначала ищут собственные векторы, а затем определяют каждое собственное значение по собственному вектору, оказывается гораздо более приемлемым для компьютеров. Самый простой алгоритм здесь состоит из выбора произвольного начального вектора и последующего многократного умножения его на матрицу (при необходимости нормализация вектора для сохранения его элементов разумного размера); это заставляет вектор сходиться к собственному вектору. Вариант вместо этого умножить вектор на ${ displaystyle (A- mu I) ^ {- 1}}$; это заставляет его сходиться к собственному вектору собственного значения, ближайшего к ${ displaystyle mu in mathbb {C}}$.

Если ${ displaystyle mathbf {v}}$ является (хорошим приближением) собственным вектором ${ displaystyle A}$, то соответствующее собственное значение может быть вычислено как

${ displaystyle lambda = { frac { mathbf {v} ^ {*} A mathbf {v}} { mathbf {v} ^ {*} mathbf {v}}}}$

куда ${ Displaystyle mathbf {v} ^ {*}}$ обозначает сопряженный транспонировать из ${ displaystyle mathbf {v}}$.

Современные методы

Эффективные и точные методы вычисления собственных значений и собственных векторов произвольных матриц не были известны до QR-алгоритм был разработан в 1961 году.^[43] Объединение Преобразование домохозяина с разложением LU приводит к алгоритму с лучшей сходимостью, чем алгоритм QR.^{[нужна цитата ]} Для больших Эрмитский разреженные матрицы, то Алгоритм Ланцоша является одним из примеров эффективного итерационный метод для вычисления собственных значений и собственных векторов, среди нескольких других возможностей.^[43]

Большинство численных методов, которые вычисляют собственные значения матрицы, также определяют набор соответствующих собственных векторов как побочный продукт вычисления, хотя иногда разработчики предпочитают отбрасывать информацию о собственном векторе, как только она больше не нужна.

Приложения

Собственные значения геометрических преобразований

В следующей таблице представлены некоторые примеры преобразований на плоскости вместе с их матрицами 2 × 2, собственными значениями и собственными векторами.

	Масштабирование	Неравномерное масштабирование	Вращение	Горизонтальный сдвиг	Гиперболическое вращение
Иллюстрация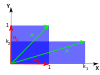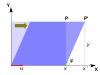
Матрица	${ displaystyle { begin {bmatrix} k & 0 0 & k end {bmatrix}}}$	${ displaystyle { begin {bmatrix} k_ {1} & 0 0 & k_ {2} end {bmatrix}}}$	${ displaystyle { begin {bmatrix} c & -s s & c end {bmatrix}}}$ ${ Displaystyle с = соз тета}$ ${ Displaystyle S = грех тета}$	${ displaystyle { begin {bmatrix} 1 & k 0 & 1 end {bmatrix}}}$	${ displaystyle { begin {bmatrix} c & s s & c end {bmatrix}}}$ ${ displaystyle c = cosh varphi}$ ${ displaystyle s = sinh varphi}$
Характеристика многочлен	${ Displaystyle ( лямбда -k) ^ {2}}$	${ Displaystyle ( лямбда -k_ {1}) ( лямбда -k_ {2})}$	${ displaystyle lambda ^ {2} -2c lambda +1}$	${ Displaystyle ( лямбда -1) ^ {2}}$	${ displaystyle lambda ^ {2} -2c lambda +1}$
Собственные значения, ${ displaystyle lambda _ {i}}$	${ displaystyle lambda _ {1} = lambda _ {2} = k}$	${ displaystyle lambda _ {1} = k_ {1}}$ ${ displaystyle lambda _ {2} = k_ {2}}$	${ displaystyle lambda _ {1} = e ^ { mathbf {i} theta} = c + s mathbf {i}}$ ${ displaystyle lambda _ {2} = e ^ {- mathbf {i} theta} = c-s mathbf {i}}$	${ displaystyle lambda _ {1} = lambda _ {2} = 1}$	${ displaystyle lambda _ {1} = e ^ { varphi}}$ ${ displaystyle lambda _ {2} = e ^ {- varphi}}$,
Алгебраический мульт., ${ Displaystyle му _ {я} = му ( лямбда _ {я})}$	${ displaystyle mu _ {1} = 2}$	${ displaystyle mu _ {1} = 1}$ ${ displaystyle mu _ {2} = 1}$	${ displaystyle mu _ {1} = 1}$ ${ displaystyle mu _ {2} = 1}$	${ displaystyle mu _ {1} = 2}$	${ displaystyle mu _ {1} = 1}$ ${ displaystyle mu _ {2} = 1}$
Геометрический мульт., ${ Displaystyle гамма _ {я} = гамма ( лямбда _ {я})}$	${ displaystyle gamma _ {1} = 2}$	${ displaystyle gamma _ {1} = 1}$ ${ displaystyle gamma _ {2} = 1}$	${ displaystyle gamma _ {1} = 1}$ ${ displaystyle gamma _ {2} = 1}$	${ displaystyle gamma _ {1} = 1}$	${ displaystyle gamma _ {1} = 1}$ ${ displaystyle gamma _ {2} = 1}$
Собственные векторы	Все ненулевые векторы	${ displaystyle { begin {align} u_ {1} & = { begin {bmatrix} 1 0 end {bmatrix}} u_ {2} & = { begin {bmatrix} 0 1 конец {bmatrix}} конец {выровненный}}}$	${ Displaystyle { begin {align} u_ {1} & = { begin {bmatrix} {} 1 - mathbf {i} end {bmatrix}} u_ {2} & = { begin {bmatrix} {} 1 + mathbf {i} end {bmatrix}} end {align}}}$	${ displaystyle u_ {1} = { begin {bmatrix} 1 0 end {bmatrix}}}$	${ Displaystyle { begin {align} u_ {1} & = { begin {bmatrix} {} 1 {} 1 end {bmatrix}} u_ {2} & = { begin {bmatrix } {} 1 - 1 end {bmatrix}}. End {align}}}$

Характеристическое уравнение вращения - это квадратное уровненеие с дискриминант ${ Displaystyle D = -4 ( грех тета) ^ {2}}$, которое является отрицательным числом всякий раз, когда θ не является целым числом, кратным 180 °. Следовательно, за исключением этих частных случаев, два собственных значения являются комплексными числами, ${ Displaystyle соз тета пм mathbf {я} грех тета}$; и все собственные векторы имеют ненастоящие элементы. В самом деле, за исключением этих частных случаев, поворот изменяет направление любого ненулевого вектора на плоскости.

Линейное преобразование, превращающее квадрат в прямоугольник той же площади ( сжатие ) имеет обратные собственные значения.

Уравнение Шредингера

В волновые функции связанный с связанные состояния из электрон в атом водорода можно рассматривать как собственные векторы гамильтониан атома водорода а также оператор углового момента. Они связаны с собственными значениями, интерпретируемыми как их энергии (возрастающие вниз: ${ Displaystyle п = 1, , 2, , 3, , ldots}$) и угловой момент (увеличивается по горизонтали: s, p, d, ...). На рисунке показан квадрат абсолютного значения волновых функций. Более яркие области соответствуют более высоким плотность вероятности на должность измерение. В центре каждой фигуры находится атомное ядро, а протон.

Пример уравнения на собственные значения, в котором преобразование ${ displaystyle T}$ представлена ​​в терминах дифференциального оператора. Уравнение Шредингера в квантовая механика:

${ Displaystyle H psi _ {E} = E psi _ {E} ,}$

куда ${ displaystyle H}$, то Гамильтониан, является вторым порядком дифференциальный оператор и ${ displaystyle psi _ {E}}$, то волновая функция, - одна из его собственных функций, соответствующая собственному значению ${ displaystyle E}$, интерпретируется как его энергия.

Однако в случае, когда вас интересует только связанное состояние решения уравнения Шредингера, ищем ${ displaystyle psi _ {E}}$ в пространстве квадратично интегрируемый функции. Поскольку это пространство Гильбертово пространство с четко определенным скалярное произведение можно ввести базисный набор в котором ${ displaystyle psi _ {E}}$ и ${ displaystyle H}$ может быть представлен как одномерный массив (т.е. вектор) и матрица соответственно. Это позволяет представить уравнение Шредингера в матричной форме.

В обозначение бюстгальтера часто используется в этом контексте. Вектор, который представляет состояние системы, в гильбертовом пространстве функций, интегрируемых с квадратом, представлен как ${ displaystyle | Psi _ {E} rangle}$. В этих обозначениях уравнение Шредингера имеет вид:

${ Displaystyle H | Psi _ {E} rangle = E | Psi _ {E} rangle}$

куда ${ displaystyle | Psi _ {E} rangle}$ является собственное состояние из ${ displaystyle H}$ и ${ displaystyle E}$ представляет собственное значение. ${ displaystyle H}$ является наблюдаемый самосопряженный оператор, бесконечномерный аналог эрмитовых матриц. Как и в матричном случае, в приведенном выше уравнении ${ Displaystyle H | Psi _ {E} rangle}$ под вектором, полученным преобразованием ${ displaystyle H}$ к ${ displaystyle | Psi _ {E} rangle}$.