Внешняя алгебра - Exterior algebra

Ориентация определяется упорядоченным набором векторов.

Перевернутая ориентация соответствует отрицанию внешнего вида продукта.

Геометрическая интерпретация оценки п элементы в реальной внешней алгебре для п = 0 (точка со знаком), 1 (направленный отрезок или вектор), 2 (элемент ориентированной плоскости), 3 (ориентированный объем). Внешний продукт п векторы можно визуализировать как любые п-размерная форма (например, п-параллелотоп, п-эллипсоид ); с величиной (гиперобъем ), и ориентация определяется его (п − 1)-мерная граница и с какой стороны находится интерьер.^[1][2]

В математика, то внешний продукт или же клин векторов - алгебраическая конструкция, используемая в геометрия учиться области, тома, и их многомерные аналоги. Внешнее произведение двух векторов ты иv, обозначаемый ты ∧ v, называется бивектор и живет в пространстве, называемом внешний квадрат, а векторное пространство которое отличается от исходного пространства векторов. В величина^[3] из ты ∧ v можно интерпретировать как площадь параллелограмма со сторонами ты иv, который в трех измерениях также можно вычислить с помощью перекрестное произведение двух векторов. Как и кросс-продукт, внешний продукт антикоммутативный, означающий, что ты ∧ v = −(v ∧ ты) для всех векторов ты и v, но, в отличие от перекрестного произведения, внешнее произведение ассоциативный. Один из способов визуализировать бивектор - это семейство параллелограммы все лежат в одной плоскости, имеют одинаковую площадь и одинаковые ориентация - выбор по часовой стрелке или против часовой стрелки.

При таком рассмотрении внешнее произведение двух векторов называется 2 лопасти. В более общем плане внешний продукт любого количества k векторов могут быть определены и иногда называются k-лезвие. Он живет в пространстве, известном как k-я внешняя мощность. Величина полученного k-blade - объем k-размерный параллелотоп ребра которого являются заданными векторами, как и величина скалярное тройное произведение векторов в трех измерениях дает объем параллелепипеда, созданный этими векторами.

В внешняя алгебра, или же Алгебра грассмана после Герман Грассманн,^[4] - алгебраическая система, произведением которой является внешний продукт. Внешняя алгебра предоставляет алгебраическую среду, в которой можно ответить на геометрические вопросы. Например, лезвия имеют конкретную геометрическую интерпретацию, а объектами внешней алгебры можно манипулировать в соответствии с набором однозначных правил. Внешняя алгебра содержит объекты, которые не только k-клинки, но суммы k-клинки; такая сумма называется k-вектор.^[5] В k-клинки, поскольку они являются простыми произведениями векторов, называются простыми элементами алгебры. В классифицировать любой k-вектор определяется как наименьшее количество простых элементов, сумма которых составляет. Внешнее произведение распространяется на всю внешнюю алгебру, поэтому имеет смысл умножать любые два элемента алгебры. С этим продуктом внешняя алгебра представляет собой ассоциативная алгебра, что обозначает α ∧ (β ∧ γ) = (α ∧ β) ∧ γ для любых элементов α, β, γ. В k-векторы имеют степень k, что означает, что они являются суммой произведений k векторы. Когда элементы разной степени умножаются, степени складываются как умножение многочлены. Это означает, что внешняя алгебра является градуированная алгебра.

Определение внешней алгебры имеет смысл для пространств не только геометрических векторов, но и других векторных объектов, таких как векторные поля или же функции. В полной общности внешнюю алгебру можно определить для модули через коммутативное кольцо, и для других структур, представляющих интерес в абстрактная алгебра. Это одна из этих более общих конструкций, в которых внешняя алгебра находит одно из своих наиболее важных приложений, где она выступает как алгебра дифференциальные формы это фундаментально в областях, где используется дифференциальная геометрия. Внешняя алгебра также обладает множеством алгебраических свойств, которые делают ее удобным инструментом в самой алгебре. Связь внешней алгебры с векторным пространством - это тип функтор на векторных пространствах, что означает, что он определенным образом совместим с линейные преобразования векторных пространств. Внешняя алгебра - один из примеров биалгебра, что означает, что его двойное пространство также имеет продукт, и этот двойной продукт совместим с внешним продуктом. Эта двойственная алгебра и есть алгебра чередующиеся полилинейные формы, а спаривание между внешней алгеброй и двойственной ей задается интерьерный продукт.

Мотивирующие примеры

Области в самолете

Площадь параллелограмма через определитель матрицы координат двух его вершин.

В Декартова плоскость р² это настоящий векторное пространство с основа состоящий из пары единичные векторы

${ displaystyle { mathbf {e}} _ {1} = { begin {bmatrix} 1 0 end {bmatrix}}, quad { mathbf {e}} _ {2} = { begin { bmatrix} 0 1 end {bmatrix}}.}$

Предположим, что

${ displaystyle { mathbf {v}} = { begin {bmatrix} a b end {bmatrix}} = a { mathbf {e}} _ {1} + b { mathbf {e}} _ {2}, quad { mathbf {w}} = { begin {bmatrix} c d end {bmatrix}} = c { mathbf {e}} _ {1} + d { mathbf {e }} _ {2}}$

пара заданных векторов в р², написанные в компонентах. Есть уникальный параллелограмм, имеющий v и ш как две его стороны. В площадь этого параллелограмма задается стандартным детерминант формула:

${ displaystyle { text {Area}} = { Bigl |} det { begin {bmatrix} { mathbf {v}} & { mathbf {w}} end {bmatrix}} { Bigr |} = { Biggl |} det { begin {bmatrix} a & c b & d end {bmatrix}} { Biggr |} = left | ad-bc right |.}$

Рассмотрим теперь внешний продукт v и ш:

${ displaystyle { begin {align} { mathbf {v}} wedge { mathbf {w}} & = (a { mathbf {e}} _ {1} + b { mathbf {e}} _ {2}) wedge (c { mathbf {e}} _ {1} + d { mathbf {e}} _ {2}) & = ac { mathbf {e}} _ {1} клин { mathbf {e}} _ {1} + ad { mathbf {e}} _ {1} wedge { mathbf {e}} _ {2} + bc { mathbf {e}} _ {2 } wedge { mathbf {e}} _ {1} + bd { mathbf {e}} _ {2} wedge { mathbf {e}} _ {2} & = left (ad-bc right) { mathbf {e}} _ {1} wedge { mathbf {e}} _ {2} end {align}}}$

где первый шаг использует закон распределения для внешний продукт, и последний использует тот факт, что внешний продукт чередуется, и в частности е₂ ∧ е₁ = −(е₁ ∧ е₂). (Тот факт, что внешний вид продукта меняется, также заставляет ${ displaystyle mathbf {e} _ {1} wedge mathbf {e} _ {1} = mathbf {e} _ {2} wedge mathbf {e} _ {2} = 0}$.) Обратите внимание, что коэффициент в этом последнем выражении является в точности определителем матрицы [v ш]. Тот факт, что это может быть положительным или отрицательным, интуитивно означает, что v и ш могут быть ориентированы против часовой стрелки или по часовой стрелке как вершины параллелограмма, которые они определяют. Такая зона называется подписанная область параллелограмма: абсолютная величина подписанной области - обычная область, а знак определяет ее ориентацию.

То, что этот коэффициент является подписанной областью, не случайно. Фактически, относительно легко увидеть, что внешний продукт должен быть связан с областью со знаком, если попытаться аксиоматизировать эту область как алгебраическую конструкцию. Подробно, если А (v, ш) обозначает знаковую область параллелограмма, пара векторов которой v и ш образуют две смежные стороны, тогда A должна удовлетворять следующим свойствам:

1. А (рv, sш) = RSА (v, ш) для любых реальных чисел р и s, поскольку изменение масштаба любой из сторон приводит к изменению масштаба области на ту же величину (а изменение направления одной из сторон меняет ориентацию параллелограмма на противоположное).
2. А (v, v) = 0, поскольку площадь выродиться параллелограмм, определяемый v (т.е. отрезок ) равен нулю.
3. А (ш, v) = −A (v, ш), поскольку поменялись ролями v и ш меняет ориентацию параллелограмма.
4. А (v + рш, ш) = А (v, ш) для любого реального числа р, поскольку добавление кратного ш к v не влияет ни на основание, ни на высоту параллелограмма и, следовательно, не сохраняет его площадь.
5. А (е₁, е₂) = 1, поскольку площадь единичного квадрата равна единице.

Перекрестное произведение (синий вектор) по отношению к внешнему продукту (светло-синий параллелограмм). Длина поперечного произведения равна длине параллельного единичного вектора (красный), поскольку размер внешнего продукта соответствует размеру контрольного параллелограмма (светло-красный).

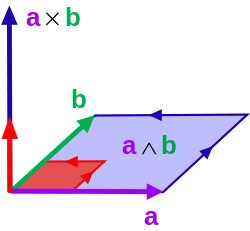
За исключением последнего свойства, внешнее произведение двух векторов удовлетворяет тем же свойствам, что и площадь. В определенном смысле внешний продукт обобщает окончательное свойство, позволяя сравнивать площадь параллелограмма с площадью любого «стандартного» выбранного параллелограмма в параллельной плоскости (здесь параллелограмм со сторонами е₁ и е₂). Другими словами, внешний вид продукта обеспечивает независимый от базиса оформление площади.^[6]

Крестовые и тройные произведения

Для векторов в 3-размерный ориентированный векторное пространство с билинейным скалярное произведение, внешняя алгебра тесно связана с перекрестное произведение и тройное произведение. Используя стандартная основа (е₁, е₂, е₃), внешнее произведение пары векторов

${ displaystyle mathbf {u} = u_ {1} mathbf {e} _ {1} + u_ {2} mathbf {e} _ {2} + u_ {3} mathbf {e} _ {3} }$

и

${ displaystyle mathbf {v} = v_ {1} mathbf {e} _ {1} + v_ {2} mathbf {e} _ {2} + v_ {3} mathbf {e} _ {3} }$

является

${ displaystyle mathbf {u} wedge mathbf {v} = (u_ {1} v_ {2} -u_ {2} v_ {1}) ( mathbf {e} _ {1} wedge mathbf { e} _ {2}) + (u_ {2} v_ {3} -u_ {3} v_ {2}) ( mathbf {e} _ {2} wedge mathbf {e} _ {3}) + (u_ {3} v_ {1} -u_ {1} v_ {3}) ( mathbf {e} _ {3} wedge mathbf {e} _ {1}),}$

куда (е₁ ∧ е₂, е₂ ∧ е₃, е₃ ∧ е₁) является базисом трехмерного пространства Λ²(р³). Коэффициенты выше такие же, как и в обычном определении перекрестное произведение векторов в трех измерениях с заданной ориентацией, единственное отличие состоит в том, что внешний продукт не является обычным вектором, а вместо этого является 2-вектор, и что внешний вид продукта не зависит от выбора ориентации.

Внесение третьего вектора

${ displaystyle mathbf {w} = w_ {1} mathbf {e} _ {1} + w_ {2} mathbf {e} _ {2} + w_ {3} mathbf {e} _ {3} ,}$

внешнее произведение трех векторов равно

${ displaystyle mathbf {u} wedge mathbf {v} wedge mathbf {w} = (u_ {1} v_ {2} w_ {3} + u_ {2} v_ {3} w_ {1} + u_ {3} v_ {1} w_ {2} -u_ {1} v_ {3} w_ {2} -u_ {2} v_ {1} w_ {3} -u_ {3} v_ {2} w_ {1 }) ( mathbf {e} _ {1} wedge mathbf {e} _ {2} wedge mathbf {e} _ {3})}$

куда е₁ ∧ е₂ ∧ е₃ является базисным вектором для одномерного пространства Λ³(р³). Скалярный коэффициент - это тройное произведение из трех векторов.

Перекрестное произведение и тройное произведение в трехмерном евклидовом векторном пространстве допускают геометрическую и алгебраическую интерпретацию. Перекрестное произведение ты × v можно интерпретировать как вектор, перпендикулярный обоим ты и v и величина которого равна площади параллелограмма, определяемой двумя векторами. Его также можно интерпретировать как вектор, состоящий из несовершеннолетние матрицы со столбцами ты и v. Тройное произведение ты, v, иш - скаляр со знаком, представляющий геометрически ориентированный объем. Алгебраически это определитель матрицы со столбцами ты, v, иш. Внешний продукт в трех измерениях допускает аналогичные интерпретации: его также можно идентифицировать с помощью ориентированных линий, областей, объемов и т. Д., Которые охватываются одним, двумя или более векторами. Внешний продукт обобщает эти геометрические понятия на все векторные пространства и на любое количество измерений, даже в отсутствие скалярного произведения.

Формальные определения и алгебраические свойства

Внешняя алгебра Λ (V) векторного пространства V через поле K определяется как фактор-алгебра из тензорная алгебра Т(V) двусторонним идеальный я генерируется всеми элементами формы Икс ⊗ Икс за Икс ∈ V (т.е. все тензоры, которые могут быть выражены как тензорное произведение вектора в V сам по себе).^[7] Идеал я содержит идеал J генерируется элементами формы ${ displaystyle x otimes y + y otimes x = (x + y) otimes (x + y) -x otimes x-y otimes y}$ и эти идеалы совпадают, если (и только если) ${ displaystyle operatorname {char} (K) neq 2}$:

${ displaystyle I supseteq J { text {с равенством iff}} operatorname {char} (K) neq 2}$.

Мы определяем

${ Displaystyle { textstyle bigwedge} (V) = T (V) / I}$

Внешний вид продукта ∧ двух элементов Λ (V) - произведение, индуцированное тензорным произведением ⊗ из Т(V). То есть, если

${ Displaystyle pi: T (V) к { textstyle bigwedge} (V) = T (V) / I}$

это каноническая сюръекция, и а и б находятся в Λ (V), то есть ${ displaystyle alpha}$ и ${ displaystyle beta}$ в Т(V) такой, что ${ Displaystyle а = пи ( альфа)}$ и ${ Displaystyle Ь = пи ( бета),}$ и

${ Displaystyle а клин b = пи ( альфа otimes beta).}$

Из определения фактор-алгебры следует, что значение ${ Displaystyle а клин б}$ не зависит от конкретного выбора ${ displaystyle alpha}$ и ${ displaystyle beta}$. У нас (по всем характеристикам) ${ displaystyle x otimes y = -y otimes x { bmod {I}}}$.

В качестве Т⁰ = K, Т¹ = V, и ${ Displaystyle влево (T ^ {0} (V) oplus T ^ {1} (V) right) cap I = {0 }}$, включения K и V в Т(V) вызвать инъекции K и V в Λ (V). Эти инъекции обычно рассматриваются как включения и называются естественные вложения, естественные инъекции или же природные включения. Слово канонический также обычно используется вместо естественный.

Альтернативный продукт

Внешний вид продукта по конструкции чередование по элементам V, что обозначает Икс ∧ Икс = 0 для всех Икс ∈ V, по приведенной выше конструкции. Отсюда следует, что продукт также антикоммутативный по элементам V, для предположения, что Икс, у ∈ V,

${ Displaystyle 0 = (х + Y) клин (х + y) = х клин х + х клин у + у клин х + у клин у = х клин у + у клин х}$

следовательно

${ Displaystyle х клин у = - (у клин х).}$

В более общем смысле, если σ это перестановка целых чисел [1, ..., k], и Икс₁, Икс₂, ..., Икс_k являются элементами V, следует, что

${ displaystyle x _ { sigma (1)} wedge x _ { sigma (2)} wedge cdots wedge x _ { sigma (k)} = operatorname {sgn} ( sigma) x_ {1} клин x_ {2} wedge cdots wedge x_ {k},}$

где sgn (σ) это подпись перестановки σ.^[8]

В частности, если Икс_я = Икс_j для некоторых я ≠ j, то имеет место и следующее обобщение альтернированности:

${ displaystyle x_ {1} wedge x_ {2} wedge cdots wedge x_ {k} = 0.}$

Внешняя мощность

В kth внешняя сила из V, обозначим Λ^k(V), это векторное подпространство из Λ (V) охватывал по элементам формы

${ displaystyle x_ {1} wedge x_ {2} wedge cdots wedge x_ {k}, quad x_ {i} in V, i = 1,2, ldots, k.}$

Если α ∈ Λ^k(V), тогда α считается k-вектор. Если, кроме того, α может быть выражено как внешний продукт k элементы V, тогда α как говорят разложимый. Хотя разложимый k-векторы охватывают Λ^k(V), не каждый элемент Λ^k(V) разложима. Например, в р⁴, следующий 2-вектор не разложим:

${ displaystyle alpha = e_ {1} wedge e_ {2} + e_ {3} wedge e_ {4}.}$

(Это симплектическая форма, поскольку α ∧ α ≠ 0.^[9])

Основа и размер

Если измерение из V является п и { е₁, ..., е_п } это основа за V, то множество

${ displaystyle {, e_ {i_ {1}} wedge e_ {i_ {2}} wedge cdots wedge e_ {i_ {k}} ~ { big |} ~~ k = 1,2, cdots n ~~ { text {и}} ~~ 1 leq i_ {1}$

это основа для Λ^k(V). Причина в следующем: учитывая любое внешнее изделие вида

${ Displaystyle v_ {1} клин cdots клин v_ {к},}$

каждый вектор v_j можно записать как линейная комбинация базисных векторов е_я; используя билинейность внешнего произведения, это можно расширить до линейной комбинации внешних произведений этих базисных векторов. Любой внешний продукт, в котором один и тот же базисный вектор встречается более одного раза, равен нулю; любой внешний продукт, в котором базисные векторы не появляются в правильном порядке, может быть переупорядочен, меняя знак всякий раз, когда два базисных вектора меняются местами. В общем, полученные коэффициенты базиса k-векторы могут быть вычислены как несовершеннолетние из матрица который описывает векторы v_j с точки зрения основы е_я.

Подсчитав базовые элементы, размерность Λ^k(V) равно a биномиальный коэффициент:

${ displaystyle dim { textstyle bigwedge} ^ {k} (V) = { binom {n} {k}} ,.}$

куда п это размер векторов, и k количество векторов в произведении. Биномиальный коэффициент дает правильный результат даже в исключительных случаях; особенно, Λ^k(V) = { 0 } за k > п.

Любой элемент внешней алгебры можно записать как сумму k-векторы. Следовательно, как векторное пространство внешняя алгебра является прямая сумма

${ displaystyle { textstyle bigwedge} (V) = { textstyle bigwedge} ^ {0} (V) oplus { textstyle bigwedge} ^ {1} (V) oplus { textstyle bigwedge} ^ {2} (V) oplus cdots oplus { textstyle bigwedge} ^ {n} (V)}$

(где по соглашению Λ⁰(V) = K, то поле лежащий в основе V, и Λ¹(V) = V), поэтому его размерность равна сумме биномиальных коэффициентов, которая равна 2^п.

Ранг k-вектор

Если α ∈ Λ^k(V), то можно выразить α как линейная комбинация разложимых k-векторы:

${ Displaystyle альфа = альфа ^ {(1)} + альфа ^ {(2)} + cdots + альфа ^ {(s)}}$

где каждый α^(я) разложим, скажем

${ Displaystyle альфа ^ {(я)} = альфа _ {1} ^ {(я)} клин cdots клин альфа _ {к} ^ {(я)}, quad я = 1,2 , ldots, s.}$

В классифицировать из k-вектор α - минимальное количество разложимых k-векторы в таком расширении α. Это похоже на понятие тензорный ранг.

Ранг особенно важен при изучении 2-векторов (Штернберг 1964, §III.6) (Bryant et al. 1991 г. ). Ранг 2-вектора α можно отождествить с половиной ранг матрицы коэффициентов α в основе. Таким образом, если е_я это основа для V, тогда α можно однозначно выразить как

${ Displaystyle альфа = сумма _ {я, j} а_ {ij} е_ {я} клин е_ {j}}$

куда а_ij = −а_джи (матрица коэффициентов имеет вид кососимметричный ). Ранг матрицы а_ij поэтому четно и в два раза выше ранга формы α.

В характеристике 0 2-вектор α имеет звание п если и только если

${ displaystyle { underset {p} { underbrace { alpha wedge cdots wedge alpha}}} neq 0 }$ и ${ displaystyle { underset {p + 1} { underbrace { alpha wedge cdots wedge alpha}}} = 0.}$

Градуированная структура

Внешний продукт k-вектор с п-вектор - это (k + п)-vector, снова вызывая билинейность. Как следствие, разложение в прямую сумму предыдущего раздела

${ Displaystyle { textstyle bigwedge} (V) = { textstyle bigwedge} ^ {! 0} (V) oplus { textstyle bigwedge} ^ {! 1} (V) oplus { textstyle bigwedge} ^ {! 2} (V) oplus cdots oplus { textstyle bigwedge} ^ {! n} (V)}$

дает внешней алгебре дополнительную структуру градуированная алгебра, то есть

${ displaystyle { textstyle bigwedge} ^ {k} (V) wedge { textstyle bigwedge} ^ {p} (V) subset { textstyle bigwedge} ^ {k + p} (V).}$

Более того, если K - базовое поле, имеем

${ Displaystyle { textstyle bigwedge} ^ {! 0} (V) = K}$ и ${ Displaystyle { textstyle bigwedge} ^ {! 1} (V) = V.}$

Внешний продукт оценивается как антикоммутативный, что означает, что если α ∈ Λ^k(V) и β ∈ Λ^п(V), тогда

${ Displaystyle альфа клин бета = (- 1) ^ {kp} бета клин альфа.}$

Помимо изучения градуированной структуры внешней алгебры, Бурбаки (1989) изучает дополнительные градуированные структуры на внешних алгебрах, например, на внешней алгебре градуированный модуль (модуль, который уже имеет свою градацию).

Универсальная собственность

Позволять V быть векторным пространством над полем K. Неформально умножение в Λ (V) выполняется путем манипулирования символами и наложения распределительный закон, ассоциативный закон, и используя идентификатор v ∧ v = 0 за v ∈ V. Формально, Λ (V) является «самой общей» алгеброй, в которой эти правила выполняются для умножения в том смысле, что любая ассоциативная единица K-алгебра, содержащая V с попеременным умножением на V должен содержать гомоморфный образ Λ (V). Другими словами, внешняя алгебра имеет следующие универсальная собственность:^[10]

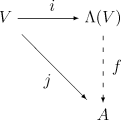
Чтобы построить наиболее общую алгебру, содержащую V и чье умножение чередуется на V, естественно начать с наиболее общей ассоциативной алгебры, содержащей V, то тензорная алгебра Т(V), а затем применить свойство чередования, взяв подходящий частное. Таким образом, мы берем двусторонний идеальный я в Т(V) генерируется всеми элементами формы v ⊗ v за v в V, и определим Λ (V) как частное

${ Displaystyle { textstyle bigwedge} (V) = T (V) / I }$

(и используйте ∧ как символ умножения в Λ (V)). Тогда несложно показать, что Λ (V) содержит V и удовлетворяет вышеуказанному универсальному свойству.

Как следствие этой конструкции, операция присвоения векторному пространству V его внешняя алгебра Λ (V) это функтор от категория векторных пространств в категорию алгебр.

Вместо того, чтобы определять Λ (V) сначала, а затем выявление внешних сил Λ^k(V) как определенные подпространства, можно альтернативно определить пространства Λ^k(V) сначала, а затем объедините их, чтобы сформировать алгебру Λ (V). Этот подход часто используется в дифференциальной геометрии и описан в следующем разделе.

Обобщения

Учитывая коммутативное кольцо р и р-модуль M, мы можем определить внешнюю алгебру Λ (M), как и выше, в качестве подходящего фактора тензорной алгебры Т(M). Он будет удовлетворять аналогичному универсальному свойству. Многие свойства Λ (M) также требуют, чтобы M быть проективный модуль. Если используется конечномерность, свойства дополнительно требуют, чтобы M быть конечно порожденный и проективный. Обобщения наиболее распространенных ситуаций можно найти в Бурбаки (1989).

Внешние алгебры векторные пакеты часто рассматриваются в геометрии и топологии. Нет никаких существенных различий между алгебраическими свойствами внешней алгебры конечномерных векторных расслоений и внешней алгеброй конечно порожденных проективных модулей за счет Теорема Серра – Свона.. Более общие внешние алгебры могут быть определены для снопы модулей.

Альтернативная тензорная алгебра

Если K - поле характеристики 0,^[11] то внешняя алгебра векторного пространства V можно канонически отождествить с векторным подпространством T (V) состоящий из антисимметричные тензоры. Напомним, что внешняя алгебра является фактором T (V) идеалом я создано Икс ⊗ Икс.

Пусть T^р(V) - пространство однородных тензоров степени р. Это натянуто на разложимые тензоры

${ displaystyle v_ {1} otimes cdots otimes v_ {r}, quad v_ {i} in V.}$

В антисимметризация (или иногда кососимметризация) разложимого тензора определяется равенством

${ displaystyle operatorname {Alt} (v_ {1} otimes cdots otimes v_ {r}) = { frac {1} {r!}} sum _ { sigma in { mathfrak {S} } _ {r}} operatorname {sgn} ( sigma) v _ { sigma (1)} otimes cdots otimes v _ { sigma (r)}}$

где сумма берется по симметричная группа перестановок символов {1, ..., р}. Это продолжается посредством линейности и однородности до операции, также обозначаемой Alt, на полной тензорной алгебре T (V). Изображение Alt (T (V)) это переменная тензорная алгебра, обозначим A (V). Это векторное подпространство в T (V), и оно наследует структуру градуированного векторного пространства от такового на T (V). Он несет ассоциативно оцененный продукт ${ displaystyle { widehat { otimes}}}$ определяется

${ displaystyle t ~ { widehat { otimes}} ~ s = operatorname {Alt} (t otimes s).}$

Хотя это произведение отличается от тензорного произведения, ядро Alt это именно идеал я (опять же, предполагая, что K имеет характеристику 0), и существует канонический изоморфизм

${ Displaystyle A (V) cong { textstyle bigwedge} (V).}$

Обозначение индекса

Предположим, что V имеет конечную размерность п, и это основа е₁, ..., е_п из V дано. то любой знакопеременный тензор т ∈ A^р(V) ⊂ Т^р(V) можно записать в индексное обозначение в качестве

${ displaystyle t = t ^ {i_ {1} i_ {2} cdots i_ {r}} , { mathbf {e}} _ {i_ {1}} otimes { mathbf {e}} _ { i_ {2}} otimes cdots otimes { mathbf {e}} _ {i_ {r}},}$

куда т^{я₁⋅⋅⋅я_р} является полностью антисимметричный в его индексах.

Внешнее произведение двух чередующихся тензоров т и s рангов р и п дан кем-то

${ displaystyle t ~ { widehat { otimes}} ~ s = { frac {1} {(r + p)!}} sum _ { sigma in { mathfrak {S}} _ {r + p}} operatorname {sgn} ( sigma) t ^ {i _ { sigma (1)} cdots i _ { sigma (r)}} s ^ {i _ { sigma (r + 1)} cdots i_ { sigma (r + p)}} { mathbf {e}} _ {i_ {1}} otimes { mathbf {e}} _ {i_ {2}} otimes cdots otimes { mathbf { e}} _ {i_ {r + p}}.}$

Компоненты этого тензора - это в точности скошенная часть компонент тензорного произведения s ⊗ т, обозначаемые квадратными скобками на индексах:

${ displaystyle (t ~ { widehat { otimes}} ~ s) ^ {i_ {1} cdots i_ {r + p}} = t ^ {[i_ {1} cdots i_ {r}} s ^ {i_ {r + 1} cdots i_ {r + p}]}.}$

Предмет интерьера также может быть описан в индексных обозначениях следующим образом. Позволять ${ Displaystyle т = т ^ {я_ {0} я_ {1} cdots я_ {г-1}}}$ - антисимметричный тензор ранга р. Тогда для α ∈ V^∗, я_αт знакопеременный тензор ранга р − 1, данный

${ displaystyle (я _ { alpha} t) ^ {i_ {1} cdots i_ {r-1}} = r sum _ {j = 0} ^ {n} alpha _ {j} t ^ {ji_ {1} cdots i_ {r-1}}.}$

куда п это размер V.

Двойственность

Альтернативные операторы

Учитывая два векторных пространства V и Икс и натуральное число k, альтернативный оператор из V^k к Икс это многолинейная карта

${ displaystyle f двоеточие V ^ {k} to X}$

так что всякий раз, когда v₁, ..., v_k находятся линейно зависимый векторов в V, тогда

${ displaystyle f (v_ {1}, ldots, v_ {k}) = 0.}$

Карта

${ displaystyle w двоеточие V ^ {k} to { textstyle bigwedge} ^ {! k} (V)}$

который ассоциируется с k векторов из V их внешний продукт, т.е. их соответствующий k-вектор, тоже чередующийся. Фактически, это отображение является «самым общим» альтернативным оператором, определенным на V^k; учитывая любой другой альтернативный оператор ж : V^k → Икс, существует единственный линейная карта φ : Λ^k(V) → Икс с ж = φ ∘ ш. Этот универсальная собственность характеризует пространство Λ^k(V) и может служить его определением.

Чередующиеся полилинейные формы

Геометрическая интерпретация для внешний продукт из п 1-формы (ε, η, ω) для получения п-form ("сетка" координатные поверхности, вот самолеты),^[12] за п = 1, 2, 3. Шоу "тиражи" ориентация.^[13][14]

Приведенное выше обсуждение специализируется на случае, когда Икс = K, базовое поле. В этом случае переменная полилинейная функция

${ displaystyle f: V ^ {k} to K }$

называется переменная полилинейная форма. Набор всех чередование полилинейные формы является векторным пространством, так как сумма двух таких отображений или произведение такого отображения на скаляр снова чередуются. В силу универсального свойства внешней силы пространство переменных форм степени k на V является естественно изоморфен двойное векторное пространство (Λ^kV)^∗. Если V конечномерна, то последняя естественно изоморфна Λ^k(V^∗). В частности, если V является п-мерный, размерность пространства чередующихся отображений из V^k к K это биномиальный коэффициент ${ displaystyle { tbinom {n} {k}}.}$

Под этой идентификацией внешний продукт принимает конкретную форму: он производит новую антисимметричную карту из двух данных. Предполагать ω : V^k → K и η : V^м → K два антисимметричных отображения. Как и в случае с тензорные произведения мультилинейных карт количество переменных в их внешнем произведении равно сумме номеров их переменных. Это определяется следующим образом:^[15]

${ displaystyle omega wedge eta = { frac {(k + m)!} {k! , m!}} operatorname {Alt} ( omega otimes eta),}$

где чередование Alt полилинейной карты определяется как среднее значение скорректированных по знаку значений по всем перестановки его переменных:

${ displaystyle operatorname {Alt} ( omega) (x_ {1}, ldots, x_ {k}) = { frac {1} {k!}} sum _ { sigma in S_ {k} } operatorname {sgn} ( sigma) , omega (x _ { sigma (1)}, ldots, x _ { sigma (k)}).}$

Это определение внешнего продукта четко определено, даже если поле K имеет конечная характеристика, если рассматривать эквивалентную версию вышеперечисленного, в которой не используются факториалы или какие-либо константы:

${ displaystyle { omega wedge eta (x_ {1}, ldots, x_ {k + m})} = sum _ { sigma in Sh_ {k, m}} operatorname {sgn} ( sigma) , omega (x _ { sigma (1)}, ldots, x _ { sigma (k)}) eta (x _ { sigma (k + 1)}, ldots, x _ { sigma ( k + m)}),}$

где здесь Ш_k,м ⊂ S_k+м это подмножество (k,м) перемешивает: перестановки σ из набора {1, 2, ..., k + м} такой, что σ(1) < σ(2) < ... < σ(k), и σ(k + 1) < σ(k + 2) < ... < σ(k + м).

Интерьерный продукт

Предположим, что V конечномерна. Если V^∗ обозначает двойное пространство в векторное пространство V, то для каждого α ∈ V^∗, можно определить антидеривация на алгебре Λ (V),

${ displaystyle i _ { alpha}: { textstyle bigwedge} ^ {k} V rightarrow { textstyle bigwedge} ^ {k-1} V.}$

Этот вывод называется интерьерный продукт с α, или иногда оператор вставки, или же сокращение к α.

Предположим, что ш ∈ Λ^kV. потом ш является полилинейным отображением V^∗ к K, поэтому он определяется своими значениями на k-складывать Декартово произведение V^∗ × V^∗ × ... × V^∗. Если ты₁, ты₂, ..., ты_k−1 находятся k − 1 элементы V^∗, затем определим

${ displaystyle (я _ { alpha} { mathbf {w}}) (u_ {1}, u_ {2}, ldots, u_ {k-1}) = { mathbf {w}} ( alpha, u_ {1}, u_ {2}, ldots, u_ {k-1}).}$

Кроме того, пусть я_αж = 0 в любое время ж является чистым скаляром (т. е. принадлежащим Λ⁰V).

Аксиоматическая характеристика и свойства

Изделие для интерьера обладает следующими свойствами:

1. Для каждого k и каждый α ∈ V^∗,

   ${ displaystyle i _ { alpha}: { textstyle bigwedge} ^ {k} V rightarrow { textstyle bigwedge} ^ {k-1} V.}$

   (Условно, Λ⁻¹V = {0}.)

2. Если v является элементом V (= Λ¹V), тогда я_αv = α(v) является двойным спариванием между элементами V и элементы V^∗.
3. Для каждого α ∈ V^∗, я_α это дифференцированный вывод степени −1:

   ${ displaystyle i _ { alpha} (a wedge b) = (i _ { alpha} a) wedge b + (- 1) ^ { deg a} a wedge (i _ { alpha} b).}$

Этих трех свойств достаточно, чтобы охарактеризовать продукт интерьера, а также определить его в общем бесконечномерном случае.

К другим свойствам предмета интерьера относятся:

• ${ displaystyle i _ { alpha} circ i _ { alpha} = 0.}$
• ${ displaystyle i _ { alpha} circ i _ { beta} = - i _ { beta} circ i _ { alpha}.}$

Двойственность Ходжа

Предположим, что V имеет конечную размерность п. Тогда внутреннее произведение индуцирует канонический изоморфизм векторных пространств

${ displaystyle { textstyle bigwedge} ^ {k} (V ^ {*}) otimes { textstyle bigwedge} ^ {n} (V) to { textstyle bigwedge} ^ {nk} (V) }$

по рекурсивному определению

${ displaystyle i _ { alpha wedge beta} = i _ { beta} circ i _ { alpha}.}$

В геометрической постановке ненулевой элемент верхней внешней мощности Λ^п(V) (которое является одномерным векторным пространством) иногда называют объемная форма (или же форма ориентации, хотя этот термин иногда может приводить к двусмысленности). Форма ориентации имени происходит из того факта, что выбор предпочтительного верхнего элемента определяет ориентацию всей внешней алгебры, поскольку это равносильно фиксации упорядоченного базиса векторного пространства. Относительно предпочтительной формы объема σ, изоморфизм между элементом ${ Displaystyle альфа в клин ^ {к} (V ^ {*})}$и его двойственный по Ходжу явно задается формулой

${ displaystyle { textstyle bigwedge} ^ {k} (V ^ {*}) to { textstyle bigwedge} ^ {n-k} (V): alpha mapsto i _ { alpha} sigma.}$

Если, помимо формы объема, векторное пространство V оснащен внутренний продукт идентификация V с V^∗, то полученный изоморфизм называется Звездный оператор Ходжа, который отображает элемент в его Ходж Дуал:

${ displaystyle star: { textstyle bigwedge} ^ {k} (V) rightarrow { textstyle bigwedge} ^ {n-k} (V).}$

Состав ${ displaystyle star}$ с собой карты Λ^k(V) → Λ^k(V) и всегда является скалярным кратным карте идентичности. В большинстве случаев объемная форма совместима с внутренним продуктом в том смысле, что это внешний продукт ортонормированный базис из V. В этом случае,

${ displaystyle star circ star: { textstyle bigwedge} ^ {k} (V) to { textstyle bigwedge} ^ {k} (V) = (- 1) ^ {k (nk) + q} mathrm {id}}$

где id - отображение идентичности, а внутренний продукт имеет метрическая подпись (п, q) — п плюсы и q минусы.

Внутренний продукт

За V конечномерное пространство, внутренний продукт (или псевдоевклидов внутренний продукт) на V определяет изоморфизм V с V^∗, а значит, и изоморфизм Λ^kV с (Λ^kV)^∗. Соединение этих двух пространств также принимает форму внутреннего продукта. О разложимых k-векторы,

${ displaystyle left langle v_ {1} wedge cdots wedge v_ {k}, w_ {1} wedge cdots wedge w_ {k} right rangle = det ( langle v_ {i} , w_ {j} rangle),}$

определитель матрицы внутренних продуктов. В частном случае v_я = ш_я, внутренний продукт - это квадратная норма k-вектор, заданный определителем Матрица грамиана (⟨v_я, v_j⟩). Затем это продолжается билинейно (или полуторалинейно в комплексном случае) до невырожденного скалярного произведения на Λ^kV. Если е_я, я = 1, 2, ..., п, для мужчин ортонормированный базис из V, то векторы вида

${ displaystyle e_ {i_ {1}} wedge cdots wedge e_ {i_ {k}}, quad i_ {1} < cdots$

составляют ортонормированный базис для Λ^k(V).

Нетрудно показать, что для векторов v₁, v₂, ... v_k в R^п, ‖V₁∧v₂∧ ... ∧v_k‖ - объем параллелепипеда, натянутого на эти векторы.

Что касается внутреннего произведения, внешнее умножение и внутреннее произведение взаимно сопряжены. В частности, для v ∈ Λ^k−1(V), ш ∈ Λ^k(V), и Икс ∈ V,

${ Displaystyle langle x клин mathbf {v}, mathbf {w} rangle = langle mathbf {v}, i_ {x ^ { flat}} mathbf {w} rangle}$

куда Икс^♭ ∈ V^∗ это музыкальный изоморфизм, линейный функционал, определяемый формулой

${ displaystyle x ^ { flat} (y) = langle x, y rangle}$

для всех у ∈ V. Это свойство полностью характеризует внутреннее произведение на внешней алгебре.

Действительно, в более общем плане для v ∈ Λ^k−л(V), ш ∈ Λ^k(V), и Икс ∈ Λ^л(V), итерация указанных выше сопряженных свойств дает

${ displaystyle langle mathbf {x} wedge mathbf {v}, mathbf {w} rangle = langle mathbf {v}, i _ { mathbf {x} ^ { flat}} mathbf { w} rangle}$

где сейчас Икс^♭ ∈ Λ^л(V^∗) ≃ (Λ^л(V))^∗ дуальный л-вектор, определяемый

${ Displaystyle mathbf {x} ^ { flat} ( mathbf {y}) = langle mathbf {x}, mathbf {y} rangle}$

для всех у ∈ Λ^л(V).

Клиффорд продукт

Для внешней алгебры, снабженной внутренним произведением, как указано выше, Клиффорд продукт вектора Икс ∈ V и ш ∈ Λ^п(V) определяется

${ displaystyle x mathbf {w} = x wedge mathbf {w} + i_ {x ^ { flat}} mathbf {w}}$

Этот продукт делает нет уважать ${ Displaystyle mathbb {Z}}$ градуировка внешней алгебры, в которой ${ Displaystyle х клин mathbf {w} in Lambda ^ {n + 1}}$ пока ${ displaystyle i_ {x ^ { flat}} mathbf {w} in Lambda ^ {n-1};}$ продукт как повышает, так и понижает степень. Произведение Клиффорда поднимается на всю внешнюю алгебру, так что для Икс ∈ Λ^k(V), это дается

${ displaystyle mathbf {xw} = mathbf {x} wedge mathbf {w} + (- 1) ^ { lfloor k / 2 rfloor} i _ { mathbf {x} ^ { flat}} mathbf {w}}$

куда ${ displaystyle lfloor m rfloor}$ обозначает функция пола, целая часть ${ displaystyle m}$. Подъем выполняется так же, как описано в предыдущем разделе. Более абстрактно, можно использовать лемму, применимую к бесплатные объекты: любой гомоморфизм, определенный на подмножестве свободная алгебра можно поднять на всю алгебру; внешняя алгебра свободна, поэтому лемма применима. Внешняя алгебра, снабженная произведением Клиффорда, называется Алгебра Клиффорда. Это соответствует тому же определению, что и в статье о Алгебры Клиффорда можно проверить, взяв билинейная форма ${ Displaystyle Q ( mathbf {x})}$ другой статьи будет ${ Displaystyle Q ( mathbf {x}) = langle mathbf {x}, mathbf {x} rangle.}$ При соответствующей артикуляции элементы алгебры Клиффорда можно понимать как спиноры, а произведение Клиффорда используется для определения действия вектора на спинор.

Внешняя алгебра также имеет ${ Displaystyle mathbb {Z} _ {2}}$ оценка, которую продукт Clifford уважает. В тензорная алгебра имеет антиавтоморфизм, называется реверсией или транспонировать, что задается картой

${ displaystyle v_ {1} otimes v_ {2} otimes cdots otimes v_ {k} mapsto v_ {k} otimes cdots otimes v_ {2} otimes v_ {1}}$

за ${ displaystyle v_ {i} in V.}$ Изучая конструкцию внешней алгебры через альтернированную тензорную алгебру ${ displaystyle operatorname {Alt} (V)}$ Как указано выше, реверсия, применяемая к чередующемуся продукту, является «просто» изменением знака или нет, в зависимости от степени:

${ Displaystyle mathbf {w} ^ {t} = (- 1) ^ { lfloor k / 2 rfloor} mathbf {w} = (- 1) ^ {k (k-1) / 2} mathbf {w}}$

Транспонирование разбивает внешнюю алгебру на четную и нечетную части. Эта классификация разделяет внутренний продукт на два отдельных продукта. Левое сокращение определяется как

${ Displaystyle langle mathbf {x} lrcorner mathbf {v}, mathbf {w} rangle = langle mathbf {v}, mathbf {x} ^ {t} wedge mathbf {w} rangle}$

пока правильное сокращение дан кем-то

${ displaystyle langle mathbf {x} llcorner mathbf {v}, mathbf {w} rangle = langle mathbf {v}, mathbf {x} wedge mathbf {w} ^ {t} rangle}$

Эти два сокращения связаны как

${ displaystyle mathbf {x} lrcorner mathbf {v} = - mathbf {v} ^ {t} llcorner mathbf {x}}$

Тогда произведение Клиффорда можно записать как

${ Displaystyle mathbf {xw} = mathbf {x} клин mathbf {w} + mathbf {x} lrcorner mathbf {w}}$

В физике чередующиеся тензоры четной степени соответствуют (вейлевским) спинорам (эта конструкция подробно описана в Алгебра Клиффорда ), из которых построены спиноры Дирака. Когда спиноры записываются с использованием записи столбец / строка, транспонирование становится просто обычным транспонированием; левое и правое сокращение можно интерпретировать как левое и правое сокращение Матрицы Дирака против спиноров Дирака. Основная полезность градуировки состоит в том, чтобы классифицировать алгебраические свойства относительно ${ Displaystyle mathbb {Z} _ {2}}$ выставление оценок; например, в Картановское разложение, где, грубо говоря, сопряжение Клиффорда соответствует Инволюция Картана.

Структура биалгебры

Существует соответствие между градуированными двойственными градуированными алгебрами Λ (V) и чередующиеся полилинейные формы на V. Внешняя алгебра (а также симметрическая алгебра ) наследует структуру биалгебры, и, действительно, Алгебра Хопфа структура, из тензорная алгебра. См. Статью о тензорные алгебры для детального рассмотрения темы.

Определенное выше внешнее произведение полилинейных форм двойственно сопродукт определенный на Λ (V), давая структуру коалгебра. В сопродукт является линейной функцией Δ: Λ (V) → Λ (V) ⊗ Λ (V) который дается

${ Displaystyle Delta (v) = 1 otimes v + v otimes 1}$

на элементах v∈V. Символ 1 обозначает единичный элемент поля. K. Напомним, что K ⊂ Λ (V), так что вышесказанное действительно лежит в Λ (V) ⊗ Λ (V). Это определение копроизведения поднимается до полного пространства Λ (V) по (линейному) гомоморфизму. Правильная форма этого гомоморфизма - это не то, что можно наивно написать, но она должна быть тщательно определена в коалгебра статья. В этом случае получаем

${ displaystyle Delta (v wedge w) = 1 otimes (v wedge w) + v otimes w-w otimes v + (v wedge w) otimes 1.}$

Подробно раскрывая это, мы получаем следующее выражение для разложимых элементов:

${ displaystyle Delta (x_ {1} wedge cdots wedge x_ {k}) = sum _ {p = 0} ^ {k} ; sum _ { sigma in Sh (p + 1, kp)} ; operatorname {sgn} ( sigma) (x _ { sigma (0)} wedge cdots wedge x _ { sigma (p)}) otimes (x _ { sigma (p + 1) } wedge cdots wedge x _ { sigma (k)}).}$

где второе суммирование ведется по всем (п+1, k−п)-тасовка. Вышеупомянутое написано с помощью нотации, чтобы отслеживать элемент поля 1: трюк состоит в том, чтобы написать ${ displaystyle x_ {0} = 1}$, и это перетасовывается в различные места во время расширения суммы путем перемешивания. Перемешивание следует непосредственно из первой аксиомы коалгебры: относительный порядок элементов ${ displaystyle x_ {k}}$ является сохранился в случайном порядке: при случайном воспроизведении упорядоченная последовательность просто разбивается на две упорядоченные последовательности, одну слева и одну справа.

Заметим, что копроизведение сохраняет градуировку алгебры. Продолжая до полного пространства Λ (V), надо

${ displaystyle Delta: { textstyle bigwedge} ^ {k} (V) to bigoplus _ {p = 0} ^ {k} { textstyle bigwedge} ^ {p} (V) otimes { textstyle bigwedge} ^ {kp} (V)}$

Символ тензора ⊗, используемый в этом разделе, следует понимать с некоторой осторожностью: это нет тот же символ тензора, который используется в определении чередующегося произведения. Интуитивно, пожалуй, проще всего представить его просто еще одним, но другим тензорным произведением: оно все еще (би-) линейное, каким должно быть тензорное произведение, но это произведение, подходящее для определения биалгебры, которое есть для создания объекта Λ (V) ⊗ Λ (V). Любые сохраняющиеся сомнения можно развеять, если поразмыслить над равенствами (1 ⊗ v) ∧ (1 ⊗ ш) = 1 ⊗ (v ∧ ш) и (v ⊗ 1) ∧ (1 ⊗ ш) = v ⊗ ш, которые следуют из определения коалгебры, в отличие от наивных манипуляций с использованием символов тензора и клина. Более подробно это различие раскрывается в статье о тензорные алгебры. Здесь проблема гораздо меньше, поскольку знакопеременное произведение Λ явно соответствует умножению в биалгебре, оставляя символ ⊗ свободным для использования в определении биалгебры. На практике это не представляет особой проблемы, если избежать фатальной ловушки замены чередующихся сумм символом клина, за одним исключением. Из ⊗ можно построить чередующийся продукт, понимая, что он работает в другом пространстве. Сразу ниже приведен пример: чередующийся продукт для двойное пространство может быть дано в терминах сопродукта. Конструкция биалгебры здесь параллельна конструкции в тензорная алгебра статья почти точно, за исключением того, что нужно правильно отслеживать знакопеременность внешней алгебры.

С точки зрения копродукта, внешний продукт в двойном пространстве является просто градуированным двойственным продуктом:

${ Displaystyle ( альфа клин бета) (x_ {1} клин cdots клин x_ {k}) = ( альфа otimes beta) left ( Delta (x_ {1} клин cdots wedge x_ {k}) right)}$

где тензорное произведение в правой части представляет собой полилинейные линейные отображения (расширенные нулем на элементы несовместимой однородной степени: точнее, α ∧ β = ε ∘ (α ⊗ β) ∘ Δ, куда ε это округ, как определено в настоящее время).

В графство гомоморфизм ε : Λ (V) → K который возвращает компонент своего аргумента с нулевой оценкой. Совместный продукт и продукт вместе с внешним продуктом определяют структуру биалгебра по внешней алгебре.

С антипод определяется на однородных элементах ${ Displaystyle S (x) = (- 1) ^ { binom {{ text {deg}} , x , + 1} {2}} x}$, внешняя алгебра, кроме того, Алгебра Хопфа.^[16]

Функциональность

Предположим, что V и W являются парой векторных пространств и ж : V → W это линейная карта. Тогда по универсальному свойству существует единственный гомоморфизм градуированных алгебр

${ Displaystyle { textstyle bigwedge} (е): { textstyle bigwedge} (V) rightarrow { textstyle bigwedge} (W)}$

такой, что

${ displaystyle { textstyle bigwedge} (f) left | _ {{ textstyle bigwedge} ^ {1} (V)} right. = f: V = { textstyle bigwedge} ^ {1} ( V) rightarrow W = { textstyle bigwedge} ^ {1} (W).}$

В частности, Λ (ж) сохраняет однородную степень. В k-градуированные компоненты Λ (ж) задаются на разложимых элементах

${ Displaystyle { textstyle bigwedge} (е) (x_ {1} клин cdots клин x_ {k}) = f (x_ {1}) клин cdots клин f (x_ {k}). }$

Позволять

${ displaystyle { textstyle bigwedge} ^ {k} (f) = { textstyle bigwedge} (f) left | _ {{ textstyle bigwedge} ^ {k} (V)} right.: { textstyle bigwedge} ^ {k} (V) rightarrow { textstyle bigwedge} ^ {k} (W).}$

Компоненты преобразования Λ^k(ж) относительно основы V и W матрица k × k несовершеннолетние ж. В частности, если V = W и V имеет конечную размерность п, то Λ^п(ж) является отображением одномерного векторного пространства Λ^пV самому себе, и поэтому задается скаляром: детерминант из ж.

Точность

Если ${ Displaystyle 0 к U к V к W к 0}$ это короткая точная последовательность векторных пространств, то

${ displaystyle 0 to { textstyle bigwedge} ^ {1} (U) wedge { textstyle bigwedge} (V) to { textstyle bigwedge} (V) to { textstyle bigwedge} ( W) до 0}$

- точная последовательность градуированных векторных пространств,^[17] как есть

${ displaystyle 0 to { textstyle bigwedge} (U) to { textstyle bigwedge} (V).}$^[18]

Прямые суммы

В частности, внешняя алгебра прямой суммы изоморфна тензорному произведению внешних алгебр:

${ displaystyle { textstyle bigwedge} (V oplus W) cong { textstyle bigwedge} (V) otimes { textstyle bigwedge} (W).}$

Это градуированный изоморфизм; т.е.

${ displaystyle { textstyle bigwedge} ^ {k} (V oplus W) cong bigoplus _ {p + q = k} { textstyle bigwedge} ^ {p} (V) otimes { textstyle bigwedge} ^ {q} (W).}$

В более общем плане, если ${ Displaystyle 0 к U к V к W к 0}$ короткая точная последовательность векторных пространств, то Λ^k(V) имеет фильтрация

${ displaystyle 0 = F ^ {0} substeq F ^ {1} substeq cdots substeq F ^ {k} substeq F ^ {k + 1} = { textstyle bigwedge} ^ {k} (V )}$

с частными

${ displaystyle F ^ {p + 1} / F ^ {p} = { textstyle bigwedge} ^ {k-p} (U) otimes { textstyle bigwedge} ^ {p} (W).}$

В частности, если U одномерно, то

${ displaystyle 0 к U otimes { textstyle bigwedge} ^ {k-1} (W) to { textstyle bigwedge} ^ {k} (V) to { textstyle bigwedge} ^ {k } (W) до 0}$

точно, и если W одномерно, то

${ displaystyle 0 to { textstyle bigwedge} ^ {k} (U) to { textstyle bigwedge} ^ {k} (V) to { textstyle bigwedge} ^ {k-1} (U ) время от W до 0}$

точно.^[19]

Приложения

Линейная алгебра

В приложениях к линейная алгебра, внешний продукт обеспечивает абстрактный алгебраический способ описания детерминант и несовершеннолетние из матрица. Например, хорошо известно, что определитель квадратной матрицы равен объему параллелоэдра, стороны которого являются столбцами матрицы (со знаком для отслеживания ориентации). Это говорит о том, что определитель может быть определенный в терминах внешнего произведения векторов-столбцов. Точно так же k × k миноры матрицы можно определить, глядя на внешние произведения выбранных векторов-столбцов k вовремя. Эти идеи можно распространить не только на матрицы, но и на линейные преобразования а также: детерминант линейного преобразования - это коэффициент, с помощью которого он масштабирует ориентированный объем любого заданного эталонного параллелоэдра. Таким образом, детерминант линейного преобразования может быть определен в терминах того, что преобразование делает с высшей внешней мощностью. Действие трансформации на меньшие внешние силы дает основа -независимый способ рассказать о несовершеннолетних трансформации.

Технические детали: Определения

Позволять^[20] ${ displaystyle V}$ быть п-мерное векторное пространство над полем ${ displaystyle K}$ с основанием ${ Displaystyle {е_ {1}, ldots, е_ {п} }}$.

• За ${ displaystyle A in operatorname {End} (V)}$, определять ${ displaystyle { textstyle bigwedge} ^ {k} A in operatorname {End} ({ textstyle bigwedge} ^ {k} V)}$ на простых тензорах

${ displaystyle { textstyle bigwedge} ^ {k} A (v_ {1} wedge cdots wedge v_ {k}) = Av_ {1} wedge cdots wedge Av_ {k}}$

и расширим определение линейно на все тензоры. В более общем плане мы можем определить ${ displaystyle { textstyle bigwedge} ^ {p} A ^ {k} in operatorname {End} ({ textstyle bigwedge} ^ {p} V), (p geq k)}$ на простых тензорах

${ displaystyle left ({ textstyle bigwedge} ^ {p} A ^ {k} right) (v_ {1} wedge cdots wedge v_ {p}) = sum _ {0 leq i_ { 1} < cdots$

т.е. выбрать k компоненты, на которых А будет действовать, а затем суммировать все результаты, полученные в результате различных выборов. Если ${ displaystyle p$, определять ${ displaystyle { textstyle bigwedge} ^ {p} A ^ {k} = 0}$. С ${ Displaystyle { textstyle bigwedge} ^ {п} V}$ одномерно с базисом ${ Displaystyle е_ {1} клин cdots клин е_ {п}}$, мы можем идентифицировать ${ displaystyle { textstyle bigwedge} ^ {n} A ^ {k}}$ с уникальным номером ${ displaystyle kappa in K}$ удовлетворение

${ displaystyle { textstyle bigwedge} ^ {n} A ^ {k} (e_ {1} wedge cdots wedge e_ {n}) = kappa (e_ {1} wedge cdots wedge e_ { n}).}$

• За ${ displaystyle varphi in operatorname {End} ({ textstyle bigwedge} ^ {p} V)}$определить внешний транспонировать ${ displaystyle varphi ^ { mathrm {T}} in operatorname {End} ({ textstyle bigwedge} ^ {n-p} V)}$ быть единственным оператором, удовлетворяющим

${ displaystyle forall omega _ {p} in { textstyle bigwedge} ^ {p} V, omega _ {np} in { textstyle bigwedge} ^ {np} V, ( varphi ^ { mathrm {T}} omega _ {np}) wedge omega _ {p} = omega _ {np} wedge ( varphi omega _ {p})}$

• За ${ displaystyle A in operatorname {End} (V)}$, определять ${ displaystyle det A = { textstyle bigwedge} ^ {n} A ^ {n}, operatorname {Tr} (A) = { textstyle bigwedge} ^ {n} A ^ {1}, operatorname {прил.} A = ({ textstyle bigwedge} ^ {n-1} A ^ {n-1}) ^ { mathrm {T}}}$. Эти определения эквивалентны другим версиям.

Основные свойства

Все результаты, полученные из других определений определителя, следа и сопряженного, могут быть получены из этого определения (поскольку эти определения эквивалентны). Вот некоторые основные свойства, связанные с этими новыми определениями:

• ${ Displaystyle ( cdot) ^ { mathrm {T}}}$ является ${ displaystyle K}$-линейный.

• ${ displaystyle (AB) ^ { mathrm {T}} = B ^ { mathrm {T}} A ^ { mathrm {T}}.}$

• У нас есть канонический изоморфизм

${ displaystyle { begin {case} psi: operatorname {End} ({ textstyle bigwedge} ^ {k} V) cong operatorname {End} ({ textstyle bigwedge} ^ {nk} V) A mapsto A ^ { mathrm {T}} end {case}}}$

Однако канонического изоморфизма между ${ displaystyle { textstyle bigwedge} ^ {k} V}$ и ${ displaystyle { textstyle bigwedge} ^ {n-k} V.}$

• ${ displaystyle operatorname {Tr} left ({ textstyle bigwedge} ^ {k} A right) = { textstyle bigwedge} ^ {n} A ^ {k}.}$ Элементы транспонированной матрицы ${ displaystyle { textstyle bigwedge} ^ {k} A}$ находятся ${ Displaystyle к раз к}$-миноры ${ displaystyle A}$.

• ${ displaystyle forall k leqslant n-1, p leqslant k, A in operatorname {End} (V),}$

${ displaystyle sum _ {q = 0} ^ {p} left ({ textstyle bigwedge} ^ {nk} A ^ {pq} right) ^ { mathrm {T}} left ({ textstyle bigwedge} ^ {k} A ^ {q} right) = left ({ textstyle bigwedge} ^ {n} A ^ {p} right) operatorname {Id} in operatorname {End} ( V).}$

Особенно,

${ displaystyle left ({ textstyle bigwedge} ^ {n-1} A ^ {p-1} right) ^ { mathrm {T}} A + left ({ textstyle bigwedge} ^ {n- 1} A ^ {p} right) ^ { mathrm {T}} = left ({ textstyle bigwedge} ^ {n} A ^ {p} right) operatorname {Id}}$

и поэтому

${ Displaystyle ( OperatorName {прил.} A) A = left ({ textstyle bigwedge} ^ {n-1} A ^ {n-1} right) ^ { mathrm {T}} A = left ({ textstyle bigwedge} ^ {n} A ^ {n} right) operatorname {Id} = ( det A) operatorname {Id}.}$

• ${ displaystyle left ({ textstyle bigwedge} ^ {n-1} A ^ {p} right) ^ { mathrm {T}} = sum _ {q = 0} ^ {p} left ( { textstyle bigwedge} ^ {n} A ^ {pq} right) (- A) ^ {q} = sum _ {q = 0} ^ {p} operatorname {Tr} left ({ textstyle bigwedge} ^ {pq} A right) (- A) ^ {q}.}$

Особенно,

${ displaystyle operatorname {прил.} A = sum _ {q = 0} ^ {n-1} left ({ textstyle bigwedge} ^ {n} A ^ {nq-1} right) (- A ) ^ {q}.}$

• ${ displaystyle operatorname {Tr} left ({ textstyle bigwedge} ^ {k} operatorname {adj} A right) = { textstyle bigwedge} ^ {n} ( operatorname {adj} A) ^ {к} = ( det A) ^ {k-1} left ({ textstyle bigwedge} ^ {n} A ^ {nk} right) = ( det A) ^ {k-1} operatorname {Tr} left ({ textstyle bigwedge} ^ {nk} A right).}$

• ${ Displaystyle OperatorName {Tr} left ( left ({ textstyle bigwedge} ^ {n-1} A ^ {k} right) ^ { mathrm {T}} right) = (nk) { textstyle bigwedge} ^ {n} A ^ {p} = (nk) operatorname {Tr} left ({ textstyle bigwedge} ^ {p} A right).}$

• Характеристический многочлен ${ displaystyle operatorname {ch} _ {A} (t)}$ из ${ displaystyle A in operatorname {End} (V)}$ может быть дан

${ displaystyle operatorname {ch} _ {A} (t) = sum _ {k = 0} ^ {n} operatorname {Tr} left ({ textstyle bigwedge} ^ {k} A right) (-t) ^ {nk} = sum _ {k = 0} ^ {n} left ({ textstyle bigwedge} ^ {n} A ^ {k} right) (- t) ^ {nk} .}$

По аналогии,

${ displaystyle operatorname {ch} _ { operatorname {adj} A} (t) = sum _ {k = 0} ^ {n} left ({ textstyle bigwedge} ^ {n} ( operatorname { adj} A) ^ {k} right) (- t) ^ {nk} = sum _ {k = 0} ^ {n} ( det A) ^ {k-1} left ({ textstyle bigwedge} ^ {n} A ^ {nk} right) (- t) ^ {nk}}$

Алгоритм Леверье

${ displaystyle { textstyle bigwedge} ^ {n} A ^ {k}}$ - коэффициенты при ${ Displaystyle (-t) ^ {п-к}}$ члены характеристического полинома. Они также появляются в выражениях ${ textstyle left ({ textstyle bigwedge} ^ {n-1} A ^ {p} right) ^ { mathrm {T}}}$ и ${ Displaystyle { textstyle bigwedge} ^ {п} ( OperatorName {прил.} A) ^ {k}}$. Алгоритм Леверье^[21] это экономичный способ вычисления ${ displaystyle { textstyle bigwedge} ^ {n} A ^ {k}}$ и ${ displaystyle { textstyle bigwedge} ^ {n-1} A ^ {k}}$:

Набор ${ displaystyle { textstyle bigwedge} ^ {n-1} A ^ {0} = 1}$;

За ${ Displaystyle к = п-1, п-2, ldots, 1,0}$,

${ displaystyle { textstyle bigwedge} ^ {n} A ^ {nk} = { frac {1} {nk}} operatorname {Tr} (A circ { textstyle bigwedge} ^ {n-1} A ^ {nk-1});}$