Параллелограмм - Википедия - Parallelogram

Параллелограмм
Этот параллелограмм представляет собой ромбовидный поскольку у него нет прямых углов и неравных сторон.
Тип	четырехугольник
Края и вершины	4
Группа симметрии	C2, [2]+, (22)
Площадь	б × час (основание × высота); ab грех θ (произведение смежных сторон и определяемого ими синуса угла при вершине)
Характеристики	выпуклый

В Евклидова геометрия, а параллелограмм это просто (несамопересекающийся ) четырехугольник с двумя парами параллельно стороны. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны. В соответствие противоположных сторон и противоположных углов является прямым следствием евклидова параллельный постулат и ни одно из условий не может быть доказано без обращения к постулату евклидовой параллельности или одной из его эквивалентных формулировок.

Для сравнения, четырехугольник с одной парой параллельных сторон - это трапеция в американском английском или трапеции в британском английском.

Трехмерный аналог параллелограмма - это параллелепипед.

Этимология (по-гречески παραλληλ-όγραμμον, parallēl-ógrammon, фигура "параллельных линий") отражает определение.

Особые случаи

Четырехугольники по симметрии

• Ромбовидный - Четырехугольник, противоположные стороны которого параллельны, а смежные стороны не равны, а углы не равны прямые углы^[1]
• Прямоугольник - Параллелограмм с четырьмя равными углами (прямыми углами).
• Ромб - Параллелограмм с четырьмя сторонами одинаковой длины.
• Квадрат - Параллелограмм с четырьмя сторонами одинаковой длины и равными углами (прямыми углами).

Характеристики

А просто (не самопересекающиеся) четырехугольник это параллелограмм если и только если верно любое из следующих утверждений:^[2][3]

• Две пары противоположных сторон параллельны (по определению).
• Две пары противоположных сторон равны по длине.
• Две пары противоположных углов равны по меру.
• В диагонали разделите друг друга пополам.
• Одна пара противоположных сторон параллельно и равной длины.
• Смежные углы находятся дополнительный.
• Каждая диагональ делит четырехугольник на две части. конгруэнтный треугольники.
• Сумма квадраты сторон равна сумме квадратов диагоналей. (Это закон параллелограмма.)
• Она имеет вращательная симметрия порядка 2.
• Сумма расстояний от любой внутренней точки до сторон не зависит от местоположения точки.^[4] (Это расширение Теорема Вивиани.)
• Есть смысл Икс в плоскости четырехугольника с тем свойством, что каждая прямая линия, проходящая через Икс делит четырехугольник на две области равной площади.^[5]

Таким образом, все параллелограммы обладают всеми перечисленными выше свойствами, и наоборот, если в простом четырехугольнике верно хотя бы одно из этих утверждений, то это параллелограмм.

Другие свойства

• Противоположные стороны параллелограмма параллельны (по определению) и поэтому никогда не пересекаются.
• Площадь параллелограмма в два раза больше площади треугольника, образованного одной из его диагоналей.
• Площадь параллелограмма также равна величине векторное произведение из двух соседний стороны.
• Любая линия, проходящая через середину параллелограмма, делит область пополам.^[6]
• Любой невырожденный аффинное преобразование переводит параллелограмм в другой параллелограмм.
• Параллелограмм имеет вращательная симметрия порядка 2 (через 180 °) (или порядка 4, если квадрат). Если в нем также есть ровно две строки отражательная симметрия тогда это должен быть ромб или продолговатый (неквадратный прямоугольник). Если он имеет четыре линии отражательной симметрии, это квадрат.
• Периметр параллелограмма равен 2 (а + б) куда а и б - длины соседних сторон.
• В отличие от любого другого выпуклого многоугольника, параллелограмм нельзя вписать ни в один треугольник, площадь которого меньше двойной его площади.^[7]
• Центры четырех квадратов, построенных либо внутри, либо снаружи на сторонах параллелограмма, являются вершинами квадрата.^[8]
• Если построить две прямые, параллельные сторонам параллелограмма одновременный к диагонали, то параллелограммы, образующиеся на противоположных сторонах этой диагонали, равны по площади.^[8]
• Диагонали параллелограмма делят его на четыре равновеликих треугольника.

Формула площади

Параллелограмм можно преобразовать в прямоугольник с такой же площадью.

Анимация для формулы площади ${ displaystyle K = bh}$.

Все формулы площади для общих выпуклых четырехугольников применимы к параллелограммам. Дальнейшие формулы относятся к параллелограммам:

Параллелограмм с основанием б и высота час можно разделить на трапеция и прямоугольный треугольник, и преобразован в прямоугольник, как показано на рисунке слева. Это означает, что площадь параллелограмма такая же, как у прямоугольника с тем же основанием и высотой:

${ displaystyle K = bh.}$

Площадь параллелограмма - это область синей области, которая является внутренней частью параллелограмма.

Формулу площади основания × высоты также можно получить, используя рисунок справа. Площадь K Параллелограмма справа (синяя область) - это общая площадь прямоугольника за вычетом площади двух оранжевых треугольников. Площадь прямоугольника

${ Displaystyle К _ { текст {rect}} = (В + А) раз Н ,}$

а площадь одного оранжевого треугольника равна

${ displaystyle K _ { text {tri}} = { frac {1} {2}} A times H. ,}$

Следовательно, площадь параллелограмма равна

${ displaystyle K = K _ { text {rect}} - 2 times K _ { text {tri}} = ((B + A) times H) - (A times H) = B times H.}$

Другая формула площади для двух сторон B и C а угол θ равен

${ Displaystyle К = В CDOT С CDOT грех тета. ,}$

Площадь параллелограмма со сторонами B и C (B ≠ C) и угол ${ displaystyle gamma}$ на пересечении диагоналей определяется выражением^[9]

${ displaystyle K = { frac {| tan gamma |} {2}} cdot left | B ^ {2} -C ^ {2} right |.}$

Когда параллелограмм задается из длин B и C двух смежных сторон вместе с длиной D₁ любой диагонали, то площадь может быть найдена из Формула Герона. Конкретно это

${ Displaystyle К = 2 { sqrt {S (S-B) (S-C) (S-D_ {1})}}}$

куда ${ Displaystyle S = (В + С + D_ {1}) / 2}$ а ведущий множитель 2 связан с тем, что выбранная диагональ делит параллелограмм на два конгруэнтные треугольники.

Площадь в декартовых координатах вершин

Пусть векторы ${ displaystyle mathbf {a}, mathbf {b} in mathbb {R} ^ {2}}$ и разреши ${ displaystyle V = { begin {bmatrix} a_ {1} & a_ {2} b_ {1} & b_ {2} end {bmatrix}} in mathbb {R} ^ {2 times 2}}$ обозначим матрицу с элементами а и б. Тогда площадь параллелограмма, порожденная а и б равно ${ displaystyle | det (V) | = | a_ {1} b_ {2} -a_ {2} b_ {1} | ,}$.

Пусть векторы ${ displaystyle mathbf {a}, mathbf {b} in mathbb {R} ^ {n}}$ и разреши ${ displaystyle V = { begin {bmatrix} a_ {1} & a_ {2} & dots & a_ {n} b_ {1} & b_ {2} & dots & b_ {n} end {bmatrix}} в mathbb {R} ^ {2 times n}}$. Тогда площадь параллелограмма, порожденная а и б равно ${ displaystyle { sqrt { det (VV ^ { mathrm {T}})}}}$.

Пусть точки ${ displaystyle a, b, c in mathbb {R} ^ {2}}$. Тогда площадь параллелограмма с вершинами в а, б и c эквивалентно абсолютному значению определителя матрицы, построенной с использованием а, б и c как строки с последним столбцом, заполненным следующим образом:

${ displaystyle K = left | det { begin {bmatrix} a_ {1} & a_ {2} & 1 b_ {1} & b_ {2} & 1 c_ {1} & c_ {2} & 1 end { bmatrix}} right |.}$

Доказательство того, что диагонали делят друг друга пополам

Чтобы доказать, что диагонали параллелограмма делят друг друга пополам, воспользуемся конгруэнтный треугольники:

${ Displaystyle угол ABE cong angle CDE}$ (чередующиеся внутренние углы равны по мере)

${ displaystyle angle BAE cong angle DCE}$ (чередующиеся внутренние углы равны по мере).

(так как это углы, которые поперечина образует с параллельные линии AB и ОКРУГ КОЛУМБИЯ).

Также сторона AB равна по длине стороне ОКРУГ КОЛУМБИЯ, так как противоположные стороны параллелограмма равны по длине.

Следовательно, треугольники ABE и CDE конгруэнтны (постулат ASA, два соответствующих угла и включенная сторона).

Следовательно,

${ displaystyle AE = CE}$

${ displaystyle BE = DE.}$

Поскольку диагонали AC и BD разделите друг друга на отрезки равной длины, диагонали делят друг друга пополам.

Отдельно, так как диагонали AC и BD разделить друг друга пополам E, точка E это середина каждой диагонали.

Решетка параллелограммов

Параллелограммы могут размещать плоскость путем перевода. Если края равны или углы прямые, симметрия решетки выше. Они представляют четыре Решетки Браве в 2-х измерениях.

Решетки

Форма	Квадрат	Прямоугольник	Ромб	Параллелограмм
Система	Квадрат (тетрагональный)	Прямоугольный (орторомбический)	Центрированный прямоугольный (орторомбический)	Косой (моноклинический)
Ограничения	α = 90 °, а = b	α = 90 °	а = б	Никто
Симметрия	p4m, [4,4], порядок 8п	pmm, [∞, 2, ∞], порядок 4п		p1, [∞+,2,∞+], порядок 2п
Форма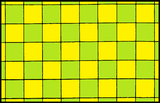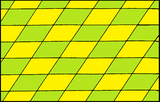

Параллелограммы, возникающие из других фигур

Доказательство без слов из Теорема Вариньона:
1. Произвольный четырехугольник и его диагонали.
2. Основания подобных треугольников параллельны голубой диагонали.
3. То же самое для красной диагонали.
4. Пары оснований образуют параллелограмм с половиной площади четырехугольника, А_q, как сумма площадей четырех больших треугольников, А_л 2 А_q (каждая из двух пар восстанавливает четырехугольник), а пара маленьких треугольников, А_s составляет четверть А_л (половина линейных размеров дает четверть площади), а площадь параллелограмма равна А_q минус А_s.

Автомедианный треугольник

An автомедианный треугольник тот, чей медианы имеют те же пропорции, что и его стороны (но в другом порядке). Если ABC - автомедианный треугольник, вершина которого А стоит напротив стороны а, грамм это центроид (где три медианы ABC пересекаются), и AL является одним из расширенных медиан ABC с L лежащий на описанном круге ABC, тогда BGCL - параллелограмм.

Вариньонный параллелограмм

В средние точки сторон произвольного четырехугольника являются вершинами параллелограмма, называемого его параллелограммом Вариньона. Если четырехугольник выпуклый или же вогнутый (то есть не самопересекающийся), то площадь параллелограмма Вариньона равна половине площади четырехугольника.

Касательный параллелограмм эллипса

Для эллипс, два диаметра называются сопрягать если и только если касательная линия к эллипсу в конце одного диаметра параллельна другому диаметру. Каждой паре сопряженных диаметров эллипса соответствует касательный параллелограмм, иногда называемый ограничивающим параллелограммом, образованный касательными линиями к эллипсу на четырех концах сопряженных диаметров. Все касательные параллелограммы данного эллипса имеют одинаковую площадь.

Возможно реконструировать эллипс из любой пары сопряженных диаметров или из любого касательного параллелограмма.

Грани параллелепипеда

А параллелепипед представляет собой трехмерную фигуру, шесть лица - параллелограммы.

Смотрите также

• Фундаментальный параллелограмм (значения)
• Антипараллелограмм

Рекомендации

внешняя ссылка

• Параллелограмм и ромб - Анимированный курс (Построение, Окружность, Площадь)
• Вайсштейн, Эрик В. "Параллелограмм". MathWorld.
• Интерактивный параллелограмм - стороны, углы и наклон
• Площадь параллелограмма в завязать узел
• Равносторонние треугольники на сторонах параллелограмма в завязать узел
• Определение и свойства параллелограмма с анимированным апплетом
• Интерактивный апплет, показывающий расчет площади параллелограмма интерактивный апплет