Гектогон - Hectogon
| Обычный гектогон | |
|---|---|
 Обычный гектогон | |
| Тип | Правильный многоугольник |
| Края и вершины | 100 |
| Символ Шлефли | {100}, т {50}, тт {25} |
| Диаграмма Кокстера | |
| Группа симметрии | Двугранный (D100), заказ 2 × 100 |
| Внутренний угол (градусы ) | 176.4° |
| Двойной многоугольник | Себя |
| Характеристики | Выпуклый, циклический, равносторонний, изогональный, изотоксальный |
В геометрия, а гектогон или гекатонтагон или 100-угольник[1][2] разносторонний многоугольник.[3][4] Сумма внутренних углов всех гектогонов составляет 17640 градусов.
Обычный гектогон
А обычный гектогон представлен Символ Шлефли {100} и может быть выполнен в виде усеченный пятиугольник, t {50}, или дважды усеченный икосипентагон, tt {25}.
Один внутренний угол в правильном гектогоне равен 176.2⁄5°, что означает, что один внешний угол будет 33⁄5°.
В площадь правильного гектогона составляет (с т = длина кромки)
и это inradius является
В по окружности правильного гектогона
Потому что 100 = 22 × 52, количество сторон содержит повторяется Ферма Прайм (в номер 5 ). Таким образом, правильный гектогон - это не конструктивный многоугольник.[5] В самом деле, его даже невозможно построить с помощью тройной угол, поскольку количество сторон не является продуктом различных Простые числа Пьерпона, ни произведение степеней двойки и тройки.[6] Неизвестно, является ли обычный гектогон neusis конструктивный.
Однако гектогон можно построить с помощью вспомогательной кривой, такой как Архимедова спираль. Угол 72 ° можно построить с помощью циркуля и линейки, поэтому возможный подход к построению одной стороны гектогона состоит в том, чтобы построить угол 72 ° с помощью циркуля и линейки, использовать спираль Архимеда, чтобы построить угол 14,4 °, и разделить пополам одну из сторон гектогона. Углы 14,4 ° дважды.
Точное построение с помощью квадратик Гиппия

Симметрия

В правильный гектогон есть Dih100 двугранная симметрия, порядок 200, представленный 100 линиями отражения. Dih100 имеет 8 диэдральных подгрупп: (Dih50, Ди25), (Dih20, Ди10, Ди5), (Dih4, Ди2, и Dih1). Также есть еще 9 циклический симметрии как подгруппы: (Z100, Z50, Z25), (Z20, Z10, Z5) и (Z4, Z2, Z1), причем Zп представляющий π /п радианная вращательная симметрия.
Джон Конвей обозначает эти более низкие симметрии буквой, а порядок симметрии следует за буквой.[7] r200 представляет собой полную симметрию и а1 этикетки не симметричны. Он дает d (диагональ) с зеркальными линиями через вершины, п с зеркальными линиями по краям (перпендикулярно), я с зеркальными линиями через вершины и края, и грамм для вращательной симметрии.
Эти более низкие симметрии позволяют степеням свободы определять нерегулярные гектогоны. Только g100 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.
Рассечение

Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на м(м-1) / 2 параллелограмма.[8]В частности, это верно для правильные многоугольники с равным числом сторон, в этом случае все параллелограммы ромбовидны. Для правильный гектогон, м= 50, его можно разделить на 1225: 25 квадратов и 24 набора по 50 ромбов. Это разложение основано на Многоугольник Петри проекция 50-куб.
 | 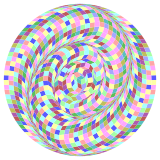 |
Гектограмм
Гектограмма - это 100-гранная звездный многоугольник. Всего 19 обычных форм[9] данный Символы Шлефли {100/3}, {100/7}, {100/9}, {100/11}, {100/13}, {100/17}, {100/19}, {100/21}, {100 / 23}, {100/27}, {100/29}, {100/31}, {100/33}, {100/37}, {100/39}, {100/41}, {100/43 }, {100/47} и {100/49}, а также 30 обычных звездные фигуры с тем же конфигурация вершины.
| Рисунок |  {100/3} |  {100/7} |  {100/11} |  {100/13} |  {100/17} |  {100/19} |
|---|---|---|---|---|---|---|
| Внутренний угол | 169.2° | 154.8° | 140.4° | 133.2° | 118.8° | 111.6° |
| Рисунок |  {100/21} |  {100/23} |  {100/27} |  {100/29} |  {100/31} |  {100/37} |
| Внутренний угол | 104.4° | 97.2° | 82.8° | 75.6° | 68.4° | 46.8° |
| Рисунок |  {100/39} |  {100/41} |  {100/43} |  {100/47} |  {100/49} | |
| Внутренний угол | 39.6° | 32.4° | 25.2° | 10.8° | 3.6° |
Смотрите также
Рекомендации
- ^ [1]
- ^ [2]
- ^ Горини, Екатерина А. (2009), Справочник фактов о геометрии файлов, Издательство Информационной базы, стр. 110, ISBN 9781438109572.
- ^ Новые элементы математики: алгебра и геометрия к Чарльз Сандерс Пирс (1976), стр.298
- ^ Конструируемый многоугольник
- ^ «Архивная копия» (PDF). Архивировано из оригинал (PDF) на 2015-07-14. Получено 2015-02-19.CS1 maint: заархивированная копия как заголовок (ссылка на сайт)
- ^ Симметрии вещей, Глава 20
- ^ Coxeter, Математические развлечения и эссе, тринадцатое издание, с.141
- ^ 19 = 50 случаев - 1 (выпуклый) - 10 (кратный 5) - 25 (кратный 2) + 5 (кратный 2 и 5)



