Гексаконтатрагон - Hexacontatetragon

Обычный гексаконатетрагон
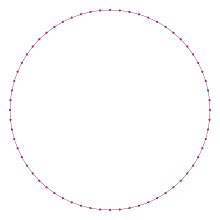Обычный гексаконатетрагон
Тип	Правильный многоугольник
Края и вершины	64
Символ Шлефли	{64}, t {32}, tt {16}, ttt {8}, tttt {4}
Диаграмма Кокстера
Группа симметрии	Двугранный (D64), заказ 2 × 64
Внутренний угол (градусы )	174.375°
Двойной многоугольник	Себя
Характеристики	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В геометрия, а гексаконатрагон (или же гексаконтакайтетрагон) или 64-угольник шестьдесят четыре стороны многоугольник. (На греческом языке приставка гексаконта- означает 60, а тетра- означает 4.) Сумма внутренних углов любого гексаконта- трагона составляет 11160 градусов.

Обычный гексаконатетрагон

В обычный гексаконатрагон можно построить как усеченный триаконтадигон, t {32}, дважды усеченный шестиугольник, tt {16}, трижды усеченный восьмиугольник, ttt {8}, четырехкратно усеченный квадрат, tttt {4} и пятикратно усеченный Digon, ttttt {2}.

Один внутренний угол в обычный гексаконатетрагон - 174³⁄₈°, что означает, что один внешний угол будет 5⁵⁄₈°.

В площадь правильного гексаконатетрагона есть (с т = длина кромки)

${ displaystyle A = 16t ^ {2} cot { frac { pi} {64}}}$

и это inradius является

${ displaystyle r = { frac {1} {2}} t cot { frac { pi} {64}}}$

В по окружности правильного гексаконатетрагона

${ displaystyle R = { frac {1} {2}} t csc { frac { pi} {64}}}$

Строительство

Поскольку 64 = 2⁶ (а сила двух ) правильный гексаконатетрагон конструктивный используя компас и линейка.^[1] Как усеченный триаконтадигон, его можно построить с помощью ребраделение пополам штатного триаконтадигона.

Симметрия

Симметрии гексаконатетрагонов

В обычный гексаконатетрагон есть Dih₆₄ двугранная симметрия, порядок 128, представленный 64 линиями отражения. Dih₆₄ имеет 6 диэдральных подгрупп: Dih₃₂, Ди₁₆, Ди₈, Ди₄, Ди₂ и Ди₁ и еще 7 циклический симметрии: Z₆₄, Z₃₂, Z₁₆, Z₈, Z₄, Z₂, а Z₁, с Z_п представляющий π /п радианная вращательная симметрия.

Эти 13 симметрий порождают 20 уникальных симметрий на правильном гексаконатетрагоне. Джон Конвей обозначает эти более низкие симметрии буквой, а порядок симметрии следует за буквой.^[2] Он дает r128 для полной отражающей симметрии Dih₆₄, и а1 без симметрии. Он дает d (диагональ) с зеркальными линиями через вершины, п с зеркальными линиями по краям (перпендикулярно), я с зеркальными линиями через вершины и края, и грамм для вращательной симметрии. а1 этикетки не симметричны.

Эти более низкие симметрии позволяют степеням свободы определять нерегулярные гексаконатетрагоны. Только g64 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.

Рассечение

64-угольник с 1740 ромбами

Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на м(м−1) / 2 параллелограмма.^[3]В частности, это верно для правильные многоугольники с равным числом сторон, в этом случае все параллелограммы ромбовидны. Для обычный гексаконатетрагон, м= 32, и его можно разделить на 496: 16 квадратов и 15 наборов по 32 ромба. Это разложение основано на Многоугольник Петри проекция 32-куб.

Примеры

Гексаконтатетраграмма

Гексаконатетраграмма - это 64-сторонняя звездный многоугольник. Есть 15 обычных форм, которые дает Символы Шлефли {64/3}, {64/5}, {64/7}, {64/9}, {64/11}, {64/13}, {64/15}, {64/17}, {64 / 19}, {64/21}, {64/23}, {64/25}, {64/27}, {64/29}, {64/31}, а также 16 составных звездные фигуры с тем же конфигурация вершины.

Обычный звездные многоугольники {64 / к}

Рисунок	{64/3}	{64/5}	{64/7}	{64/9}	{64/11}	{64/13}	{64/15}	{64/17}
Внутренний угол	163.125°	151.875°	140.625°	129.375°	118.125°	106.875°	95.625°	84.375°
Рисунок	{64/19}	{64/21}	{64/23}	{64/25}	{64/27}	{64/29}	{64/31}
Внутренний угол	73.125°	61.875°	50.625°	39.375°	28.125°	16.875°	5.625°

Рекомендации

• Именование многоугольников и многогранников