Пентаконтагон - Pentacontagon

Обычный пятиугольник
Обычный пятиугольник
Тип	Правильный многоугольник
Края и вершины	50
Символ Шлефли	{50}, т {25}
Диаграмма Кокстера
Группа симметрии	Двугранный (D50), заказ 2 × 50
Внутренний угол (градусы )	172.8°
Двойной многоугольник	Себя
Характеристики	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В геометрия, а пятиугольник или же пятиугольник или 50-угольник - это пятидесятиугольник многоугольник.^[1][2] Сумма внутренних углов любого пятиугольника составляет 8640 градусов.

А обычный пятиугольник представлен Символ Шлефли {50} и может быть построен как квазирегулярный усеченный icosipentagon, t {25}, в котором чередуются два типа ребер.

Свойства обычного пятиугольника

Один внутренний угол в правильном пятиугольнике равен 172.⁴⁄₅°, что означает, что один внешний угол будет 7¹⁄₅°.

В площадь правильного пятиугольника есть (с т = длина кромки)

${ displaystyle A = { frac {25} {2}} t ^ {2} cot { frac { pi} {50}}}$

и это inradius является

${ displaystyle r = { frac {1} {2}} t cot { frac { pi} {50}}}$

В по окружности правильного пятиугольника

${ displaystyle R = { frac {1} {2}} t csc { frac { pi} {50}}}$

Поскольку 50 = 2 × 5², правильный пятиугольник не конструктивный используя компас и линейка,^[3] и не может быть сконструирован, даже если использование тройной угол позволено.^[4] Однако его можно построить с помощью вспомогательной кривой (такой как квадратик Гиппия или Архимедова спираль ), поскольку такие кривые можно использовать для разделения углов на любое количество равных частей. Например, можно построить угол 36 °, используя циркуль и линейку, и приступить к его квинтисекции (разделить на пять равных частей) с помощью спирали Архимеда, получив угол 7,2 °, необходимый для построения пятиугольника.

Симметрия

Симметрии правильного пятиугольника. Голубыми линиями показаны подгруппы индекса 2. 3 подграфа в рамке позиционно связаны подгруппами индекса 5.

В правильный пятиугольник есть Dih₅₀ двугранная симметрия, порядок 100, представленный 50 линиями отражения. Dih₅₀ имеет 5 диэдральных подгрупп: Dih₂₅, (Dih₁₀, Ди₅) и (Dih₂, Ди₁). Также есть еще 6 циклический симметрии как подгруппы: (Z₅₀, Z₂₅), (Z₁₀, Z₅) и (Z₂, Z₁), причем Z_п представляющий π /п радианная вращательная симметрия.

Джон Конвей обозначает эти более низкие симметрии буквой, а порядок симметрии следует за буквой.^[5] Он дает d (диагональ) с зеркальными линиями через вершины, п с зеркальными линиями по краям (перпендикулярно), я с зеркальными линиями через вершины и края, и грамм для вращательной симметрии. а1 этикетки не симметричны.

Эти более низкие симметрии позволяют степеням свободы определять неправильные пятиугольники. Только g50 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.

Рассечение

50-угольник с 1200 ромбами

Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на м(м-1) / 2 параллелограмма.^[6]В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. Для правильный пятиугольник, м= 25, его можно разделить на 300: 12 наборов по 25 ромбов. Это разложение основано на Многоугольник Петри проекция 25-куб.

Примеры

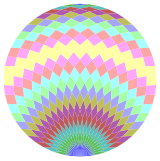Пентаконтаграмма

Пентаконтаграмма - это 50-гранная звездный многоугольник. Есть 9 обычных форм, которые дает Символы Шлефли {50/3}, {50/7}, {50/9}, {50/11}, {50/13}, {50/17}, {50/19}, {50/21} и { 50/23}, а также 16 составных звездные фигуры с тем же конфигурация вершины.

Обычный звездные многоугольники {50 / к}

Рисунок	{​50⁄3}	{​50⁄7}	{​50⁄9}	{​50⁄11}	​50⁄13
Внутренний угол	158.4°	129.6°	115.2°	100.8°	86.4°
Рисунок	{​50⁄17 }	{​50⁄19 }	{​50⁄21 }	{​50⁄23 }
Внутренний угол	57.6°	43.2°	28.8°	14.4°

Рекомендации

• Вайсштейн, Эрик В. «Пентаконтагон». MathWorld.
• Именование многоугольников и многогранников
• Пятидесятник